Čakacia
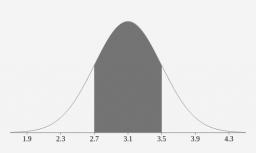
Čakacia doba v bufete sa riadi normálnym rozdelením so strednou hodnotou 130 sekúnd a rozptylom 400. Aká bude pravdepodobnosť, že niekto bude čakať menej ako minútu a pol?
Výsledok
Výsledok
Napíšte nám komentár ku príkladu a riešeniu (napríklad ak je stále niečo nejasné...):
Zobrazujem 1 komentár:
Na vyriešenie tohto príkladu sú potrebné tieto znalosti z matematiky:
Ďaľšie podobné príklady:
- Životnosť
Životnosť žiaroviek má normálne rozdelenie so strednou hodnotou 2000 hodín a so smerodajnou odchýlkou 200 hodín. Aká je pravdepodobnosť, že žiarovka vzdrží svietiť aspoň 2100 hodín? - Normálne rozloženie
Na jednej strednej škole sú známky normálne distribuované s priemerom 3,1 a štandardnou odchýlkou 0,4. Aké percento študentov na vysokej škole majú známky medzi 2,7 a 3,5? - SD - priemer
Priemer je 10 a štandardná odchýlka je 3,5. V prípade, že súbor dát obsahuje 40 hodnôt, približne, koľko hodnôt bude pohybovať v rozmedzí 6,5 až 13,5? - Štatistický príklad
Vypočítajte v súbore pacientov (priložená tabuľka 1) A) pomocou tabuľkového editora EXCEL B) programom „Social Science Statistics Calculator“ (SSSC) na web stránke a) priemerný vek pacientov a smerodajnú odchýlku (STDEV) b) priemernú dobu hospitalizác - Pre štatistický
Pre štatistický súbor 2.3; 3.4; 1.8; 3.2; 3.2; 1.9; 3.3; 4.5; 4.3; 5.0; 4.8; 4.3; 4.3; 1.9 určte výberový rozptyl a medián, a z empirickej distribučnej funkcie určte P(2.1 < ξ < 3.5). - Kontrolór
Výstupný kontrolór podniku pri kontrole 50 náhodne vybraných výrobkov zistila, že 37 z nich nemá žiadnu vadu, 8 má len jednu chybu, na troch výrobkoch zistila dve chyby a na dvoch výrobkoch boli vady celkom tri. Určite smerodajnú odchýlku a variačný koefic - Variabilita
V sledovanom období boli počty nepodarkov u dvoch smien nasledovnej: ranné smena: 2; 0; 6; 10; 2; 2; 4; 2; 5; 2; popoludňajšia smena: 4; 4; 0; 2; 10; 2; 6; 2; 3; 10; Porovnajte variabilitu u oboch smien, porovnajte priemerný počet nepodarkov o oboch smie - Priemerná
Aká je priemerná rýchlosť automobilu, ak polovicu prejdenej dráhy prešiel rýchlosťou 66 km/h a druhú polovicu rýchlosťou 86 km/h. - Ťažisko
Hmotné body sú rozložené v priestore nasledovne - zadané súradnice v priestore a ich hmotnosti. Nájdite polohu ťažiska tejto sústavy hmotných bodov: A1 [2; 19; 13] m1 = 3.7 kg A2 [15; -9; -16] m2 = 1.9 kg A- Obsah PT
Určite obsah pravouhlého trojuholníka, ktorého prepona má dĺžku 10 a jeden jej úsek (ktorý vytína výška) 4.- Inflácia
Kde bolo, tam bolo, cár vlastnil tlačiareň na peniaze a tlačil a tlačil. Výsledkom tlačenia peňazí bolo že v prvom roku ceny stúpli o 3.9%, v druhom o 6%, v treťom o 4.7% a vo štvrtom roku vládnutia o 5.5%. Potom už cár nebol zvolený. Vypočítajte priemern- Bazén
Ak do bazénu priteká voda súčasne dvoma prívodmi, naplní sa celý za 18 hodín. Jedným prívodom sa naplní o 10 hodín neskôr ako druhým. Za aký čas sa naplní bazén jednotlivými prívodmi zvlášť?- Obsah PT
V pravouhlom trojuholníku majú kolmé priemety odvesien na preponu dĺžku 7 cm a 12 cm. Určite plošný obsah trojuholníka.- Geometrický priemer
Vypočítajte geometrický priemer čísel a=11.4 a b=22. Určite priemer aj konštrukčne, ak a,b sú dĺžky úsečiek.- Ročné príjmy
Ročné príjmy (v tisícoch eur) pätnástich rodín sú: 60, 80, 90, 96, 120, 150, 200, 360, 480, 520, 1060, 1200, 1450, 2500, 7200 Vypočítajte harmonický a geometrický priemer týchto príjmov rodín.- Vysvedčenie
V triede je 31 žiakov. Z matematiky nebola na vysvedčení horšia známka než 2. Priemer známok z matematiky bol 2. Koľko žiakov malo jednotku a koľko dvojku?- Voda
Zmiešajte 20 l vody, ktorá má teplotu 53 °C, 27 l vody teplej 86 °C a 11 vody teplej 49 °C. Aká je teplota zmiešanej vody ihneď po zmiešaní? - Obsah PT
Životnosť žiaroviek má normálne rozdelenie so strednou hodnotou 2000 hodín a so smerodajnou odchýlkou 200 hodín. Aká je pravdepodobnosť, že žiarovka vzdrží svietiť aspoň 2100 hodín?
Na jednej strednej škole sú známky normálne distribuované s priemerom 3,1 a štandardnou odchýlkou 0,4. Aké percento študentov na vysokej škole majú známky medzi 2,7 a 3,5?
Priemer je 10 a štandardná odchýlka je 3,5. V prípade, že súbor dát obsahuje 40 hodnôt, približne, koľko hodnôt bude pohybovať v rozmedzí 6,5 až 13,5?
Vypočítajte v súbore pacientov (priložená tabuľka 1) A) pomocou tabuľkového editora EXCEL B) programom „Social Science Statistics Calculator“ (SSSC) na web stránke a) priemerný vek pacientov a smerodajnú odchýlku (STDEV) b) priemernú dobu hospitalizác
Pre štatistický súbor 2.3; 3.4; 1.8; 3.2; 3.2; 1.9; 3.3; 4.5; 4.3; 5.0; 4.8; 4.3; 4.3; 1.9 určte výberový rozptyl a medián, a z empirickej distribučnej funkcie určte P(2.1 < ξ < 3.5).
Výstupný kontrolór podniku pri kontrole 50 náhodne vybraných výrobkov zistila, že 37 z nich nemá žiadnu vadu, 8 má len jednu chybu, na troch výrobkoch zistila dve chyby a na dvoch výrobkoch boli vady celkom tri. Určite smerodajnú odchýlku a variačný koefic
V sledovanom období boli počty nepodarkov u dvoch smien nasledovnej: ranné smena: 2; 0; 6; 10; 2; 2; 4; 2; 5; 2; popoludňajšia smena: 4; 4; 0; 2; 10; 2; 6; 2; 3; 10; Porovnajte variabilitu u oboch smien, porovnajte priemerný počet nepodarkov o oboch smie
Aká je priemerná rýchlosť automobilu, ak polovicu prejdenej dráhy prešiel rýchlosťou 66 km/h a druhú polovicu rýchlosťou 86 km/h.
Hmotné body sú rozložené v priestore nasledovne - zadané súradnice v priestore a ich hmotnosti. Nájdite polohu ťažiska tejto sústavy hmotných bodov: A1 [2; 19; 13] m1 = 3.7 kg A2 [15; -9; -16] m2 = 1.9 kg A
Určite obsah pravouhlého trojuholníka, ktorého prepona má dĺžku 10 a jeden jej úsek (ktorý vytína výška) 4.
Kde bolo, tam bolo, cár vlastnil tlačiareň na peniaze a tlačil a tlačil. Výsledkom tlačenia peňazí bolo že v prvom roku ceny stúpli o 3.9%, v druhom o 6%, v treťom o 4.7% a vo štvrtom roku vládnutia o 5.5%. Potom už cár nebol zvolený. Vypočítajte priemern
Ak do bazénu priteká voda súčasne dvoma prívodmi, naplní sa celý za 18 hodín. Jedným prívodom sa naplní o 10 hodín neskôr ako druhým. Za aký čas sa naplní bazén jednotlivými prívodmi zvlášť?
V pravouhlom trojuholníku majú kolmé priemety odvesien na preponu dĺžku 7 cm a 12 cm. Určite plošný obsah trojuholníka.
Vypočítajte geometrický priemer čísel a=11.4 a b=22. Určite priemer aj konštrukčne, ak a,b sú dĺžky úsečiek.
Ročné príjmy (v tisícoch eur) pätnástich rodín sú: 60, 80, 90, 96, 120, 150, 200, 360, 480, 520, 1060, 1200, 1450, 2500, 7200 Vypočítajte harmonický a geometrický priemer týchto príjmov rodín.
V triede je 31 žiakov. Z matematiky nebola na vysvedčení horšia známka než 2. Priemer známok z matematiky bol 2. Koľko žiakov malo jednotku a koľko dvojku?
Zmiešajte 20 l vody, ktorá má teplotu 53 °C, 27 l vody teplej 86 °C a 11 vody teplej 49 °C. Aká je teplota zmiešanej vody ihneď po zmiešaní?