Goniometria a trigonometria - príklady - strana 8 z 32
Počet nájdených príkladov: 626
- Tri palice
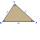 Loonie má tri drevené palice s rozmermi 17 palcov, 21 palcov a 25 palcov. Položí ich tak, aby vytvorili trojuholník. Nájdite veľkosť uhla ohraničeného stranami 17 palcov a 21 palcov. (Vyjadrite odpovede s presnosťou na stotiny) (pomocou kosínusovej vety)
Loonie má tri drevené palice s rozmermi 17 palcov, 21 palcov a 25 palcov. Položí ich tak, aby vytvorili trojuholník. Nájdite veľkosť uhla ohraničeného stranami 17 palcov a 21 palcov. (Vyjadrite odpovede s presnosťou na stotiny) (pomocou kosínusovej vety) - Vzdialenosť A-B
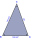 Adam (A) stojí na jednom brehu rieky, Bedrich (B) stojí na druhom. Aby mohla byť stanovená ich vzdialenosť, bola na jednom brehu rieky zmeraná základňa AC o dĺžke 136 m a uhly CAB s veľkosťou 70°21' a ACB s veľkosťou 43°44'. Aká je vzdialenosť Adama a Bed
Adam (A) stojí na jednom brehu rieky, Bedrich (B) stojí na druhom. Aby mohla byť stanovená ich vzdialenosť, bola na jednom brehu rieky zmeraná základňa AC o dĺžke 136 m a uhly CAB s veľkosťou 70°21' a ACB s veľkosťou 43°44'. Aká je vzdialenosť Adama a Bed - V trojuholníku 10
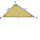 V trojuholníku ABC vypočítajte veľkosti všetkých výšok, uhlov, obvod a obsah, ak je dané a-40cm, b-57cm, c-59cm
V trojuholníku ABC vypočítajte veľkosti všetkých výšok, uhlov, obvod a obsah, ak je dané a-40cm, b-57cm, c-59cm - Deltoid 2
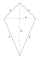 Papierový šarkan má tvar deltoidu ABCD, v ktorom sú dve kratšie strany dlhé po 30 cm, dve dlhšie strany po 51 cm a kratšia uhlopriečka má dĺžku 48 cm. Určte veľkosti vnútorných uhlov daného deltoidu.
Papierový šarkan má tvar deltoidu ABCD, v ktorom sú dve kratšie strany dlhé po 30 cm, dve dlhšie strany po 51 cm a kratšia uhlopriečka má dĺžku 48 cm. Určte veľkosti vnútorných uhlov daného deltoidu. - Plocha 6
 Plocha na výcvik streľby má tvar lichobežníka, ktorého rovnobežné strany sú dlhé 36m, 21m, zvyšné strany majú dĺžku 14m, 16m. Určte veľkosť vnútorných uhlov pri dlhšej základni.
Plocha na výcvik streľby má tvar lichobežníka, ktorého rovnobežné strany sú dlhé 36m, 21m, zvyšné strany majú dĺžku 14m, 16m. Určte veľkosť vnútorných uhlov pri dlhšej základni. - Dve horárne
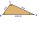 Dve horárne A, B sú oddelené lesom, obe sú viditeľné z horárne C, ktorá je s oboma spojená priamymi cestami. Akú bude mať dĺžku projektovaná cesta z A do B, ak je AC = 5004 m, BC = 2600 m a uhol ABC = 53° 45 '?
Dve horárne A, B sú oddelené lesom, obe sú viditeľné z horárne C, ktorá je s oboma spojená priamymi cestami. Akú bude mať dĺžku projektovaná cesta z A do B, ak je AC = 5004 m, BC = 2600 m a uhol ABC = 53° 45 '? - V rovnobežníku 2
 V rovnobežníku je súčet dĺžok strán a+b = 234. Uhol zovretý stranami a a b je 60°. Dĺžka uhlopriečky proti danému uhlu 60° je u=162. Vypočítajte strany rovnobežníka, jeho obvod a obsah.
V rovnobežníku je súčet dĺžok strán a+b = 234. Uhol zovretý stranami a a b je 60°. Dĺžka uhlopriečky proti danému uhlu 60° je u=162. Vypočítajte strany rovnobežníka, jeho obvod a obsah. - Z okna 2
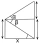 Z okna ležiaceho 8 m nad horizontálnou rovinou vidíme vrchol veže vo výškovom uhle 53 stupňov 20 minút, jej pätu v hĺbkovom uhle 14 stupňov 15 minút. Aká vysoká je veža?
Z okna ležiaceho 8 m nad horizontálnou rovinou vidíme vrchol veže vo výškovom uhle 53 stupňov 20 minút, jej pätu v hĺbkovom uhle 14 stupňov 15 minút. Aká vysoká je veža? - Goniometrická rovnica
 Vyriešte goniometrickú rovnicu: sin4 θ - 1/cos² θ=cos² θ - 2
Vyriešte goniometrickú rovnicu: sin4 θ - 1/cos² θ=cos² θ - 2 - Stred prepony
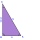 Pre vnútorné uhly trojuholnika ABC platí, že alfa beta a gama sú v pomere 1:2:3. Najdlhšia strana trojuholníka AB má dĺžku 30cm. Vypočítaj obvod trojuholnika CBS, ak S je stred strany AB
Pre vnútorné uhly trojuholnika ABC platí, že alfa beta a gama sú v pomere 1:2:3. Najdlhšia strana trojuholníka AB má dĺžku 30cm. Vypočítaj obvod trojuholnika CBS, ak S je stred strany AB - Zorný uhol 2
 Pozorovateľ vidí priamu ohradu dlhú 60 m v zornom uhle 30°. Od jedného konca ohrady je vzdialený 102 m. Ako ďaleko je pozorovateľ od druhého konca ohrady?
Pozorovateľ vidí priamu ohradu dlhú 60 m v zornom uhle 30°. Od jedného konca ohrady je vzdialený 102 m. Ako ďaleko je pozorovateľ od druhého konca ohrady? - Šírka kanála
 Priečny rez kanála má tvar lichobežníka. Šírka dna je 2,25 m a hĺbka 5 m. Steny majú sklon 68° 12' a 73° 45'. Vypočítajte hornú šírku kanála.
Priečny rez kanála má tvar lichobežníka. Šírka dna je 2,25 m a hĺbka 5 m. Steny majú sklon 68° 12' a 73° 45'. Vypočítajte hornú šírku kanála. - Ťažisko a obsah
 V trojuholníku ABC sú dané dĺžky jeho ťažníc tc=9, ta=6. Označme T priesečník ťažníc, S stred strany BC. Veľkosť uhla CTS je 60°. Vypočítajte dĺžku strany BC s presnosťou na 2 desatinné miesta
V trojuholníku ABC sú dané dĺžky jeho ťažníc tc=9, ta=6. Označme T priesečník ťažníc, S stred strany BC. Veľkosť uhla CTS je 60°. Vypočítajte dĺžku strany BC s presnosťou na 2 desatinné miesta - Stĺp elektrického vedenia
 Z miesta A je vidieť stĺp elektrického vedenia pod uhlom 18 stupňov. Z miesta B, do ktorého sa dostaneme, ideme Ak z Miesta A 30m smerom od stĺpu pod uhlom 10 stupňov. Urči výšku stĺpa elektrického vedenia.
Z miesta A je vidieť stĺp elektrického vedenia pod uhlom 18 stupňov. Z miesta B, do ktorého sa dostaneme, ideme Ak z Miesta A 30m smerom od stĺpu pod uhlom 10 stupňov. Urči výšku stĺpa elektrického vedenia. - V oblakoch
 Z dvoch miest A a B na vodorovnej rovine bolo pozorované čelo mraku nad spojnicou obidvoch miest pod výškovým uhlom 73°20' a 64°40'. Miesta A a B sú od seba vzdialené 2830 m. Ako vysoko je mrak?
Z dvoch miest A a B na vodorovnej rovine bolo pozorované čelo mraku nad spojnicou obidvoch miest pod výškovým uhlom 73°20' a 64°40'. Miesta A a B sú od seba vzdialené 2830 m. Ako vysoko je mrak? - Vypočítajte 24
 Vypočítajte obsah pravidelného 15-uholníka vpísaného do kružnice s polomerom r = 4 . Výsledok uveďte s presnosťou na dve desatinné miesta.
Vypočítajte obsah pravidelného 15-uholníka vpísaného do kružnice s polomerom r = 4 . Výsledok uveďte s presnosťou na dve desatinné miesta. - Spoločná tetiva
 Spoločná tetiva dvoch kružníc k1 a k2 má dĺžku 3,8 cm. Táto tetiva zviera s polomerom r1 kružnice k1 uhol o veľkosti 47° a s polomerom r2 kružnice k2 uhol 24° 30 '. Vypočítajte oba polomery a vzdialenosť oboch stredov kružníc.
Spoločná tetiva dvoch kružníc k1 a k2 má dĺžku 3,8 cm. Táto tetiva zviera s polomerom r1 kružnice k1 uhol o veľkosti 47° a s polomerom r2 kružnice k2 uhol 24° 30 '. Vypočítajte oba polomery a vzdialenosť oboch stredov kružníc. - Tetivy pod uhlom
 Z bodu na kružnici s priemerom 8 cm sú vedené dve zhodné tetivy, ktoré zvierajú uhol 60°. Vypočítaj dĺžku týchto tetív.
Z bodu na kružnici s priemerom 8 cm sú vedené dve zhodné tetivy, ktoré zvierajú uhol 60°. Vypočítaj dĺžku týchto tetív. - V štvorci
 V štvorci ABCD so stranou a = 6 cm je bod E stred strany AB a bod F stred strany BC. Vypočítajte veľkosť všetkých uhlov trojuholníka DEF a dĺžky jeho strán.
V štvorci ABCD so stranou a = 6 cm je bod E stred strany AB a bod F stred strany BC. Vypočítajte veľkosť všetkých uhlov trojuholníka DEF a dĺžky jeho strán. - Kružnica - stredový
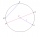 Je daná kružnica o polomere 10 cm a jej tetiva, ktorá má dĺžku 12 cm. Vypočítajte veľkosť stredového uhla, ktorý tejto tetive prislúcha.
Je daná kružnica o polomere 10 cm a jej tetiva, ktorá má dĺžku 12 cm. Vypočítajte veľkosť stredového uhla, ktorý tejto tetive prislúcha.
Máš úlohu, ktorú si tu nenašiel vyriešenú? Pošli nám túto úlohu a my Ti ju skúsime vypočítať. Riešime príklady a úlohy z matematiky. Nielen domáce.
