Pytagorova veta + prevody jednotiek - príklady a úlohy
Počet nájdených príkladov: 133
- Tetiva 22
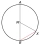 Tetiva kružnice je dlhá 233 a dĺžka kružnicového oblúka nad tetivou 235. Aký je polomer kružnice a aká stredový uhol prislúchajúci kružnicovému oblúku?
Tetiva kružnice je dlhá 233 a dĺžka kružnicového oblúka nad tetivou 235. Aký je polomer kružnice a aká stredový uhol prislúchajúci kružnicovému oblúku? - Vrcholy T3D
 Vrcholy trojuholníka ABC sú: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Vypočítajte dĺžky strán AB, AC a uhol pri vrchole A.
Vrcholy trojuholníka ABC sú: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Vypočítajte dĺžky strán AB, AC a uhol pri vrchole A. - V trojuholníku 16
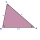 V trojuholníku ABC poznáme a = 4 cm, b = 6 cm, γ = 60°. Vypočítajte obsah, polomer vpísanej a opísanej kružnice.
V trojuholníku ABC poznáme a = 4 cm, b = 6 cm, γ = 60°. Vypočítajte obsah, polomer vpísanej a opísanej kružnice. - Rebrík 15
 Rebrík dlhý 6,5 m je opretý o zvislú stenu. Jeho spodný koniec sa opiera o zem vo vzdialenosti 1,6 m od steny. Určte, do akej výšky dosahuje horný koniec rebríka a pod akým uhlom je rebrík opretý o stenu.
Rebrík dlhý 6,5 m je opretý o zvislú stenu. Jeho spodný koniec sa opiera o zem vo vzdialenosti 1,6 m od steny. Určte, do akej výšky dosahuje horný koniec rebríka a pod akým uhlom je rebrík opretý o stenu.
- Archeologovia 2
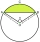 Archeológovia potrebujú zistiť veľkosť nádoby, ak nájdeny črep bol v tvare kruhového odseku s dĺžkou 12 cm a výškou 3 cm. Aký je obsah tohto odseku?
Archeológovia potrebujú zistiť veľkosť nádoby, ak nájdeny črep bol v tvare kruhového odseku s dĺžkou 12 cm a výškou 3 cm. Aký je obsah tohto odseku? - V trojuholníku 18
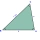 V trojuholníku ABC je dané b=5 cm, c=6 cm, /BAC/ = 80°. Vypočítajte veľkosti ostatných strán a uhlov, ďalej určte veľkosti ťažnice tc a obsah trojuholníka.
V trojuholníku ABC je dané b=5 cm, c=6 cm, /BAC/ = 80°. Vypočítajte veľkosti ostatných strán a uhlov, ďalej určte veľkosti ťažnice tc a obsah trojuholníka. - Plocha 6
 Plocha na výcvik streľby má tvar lichobežníka, ktorého rovnobežné strany sú dlhé 36m, 21m, zvyšné strany majú dĺžku 14m, 16m. Určte veľkosť vnútorných uhlov pri dlhšej základni.
Plocha na výcvik streľby má tvar lichobežníka, ktorého rovnobežné strany sú dlhé 36m, 21m, zvyšné strany majú dĺžku 14m, 16m. Určte veľkosť vnútorných uhlov pri dlhšej základni. - Daný je 8
 Daný je rovnobežnik KLMN, v ktorom poznáme veľkosti strán/KL/ = a = 84,5 cm, /KN/ = 47,8 cm a veľkosť uhla pri vrchole K 56°40´. Vypočítajte veľkosť uhlopriečok.
Daný je rovnobežnik KLMN, v ktorom poznáme veľkosti strán/KL/ = a = 84,5 cm, /KN/ = 47,8 cm a veľkosť uhla pri vrchole K 56°40´. Vypočítajte veľkosť uhlopriečok. - Štvoruholník 13
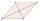 Štvoruholník ABCD je súmerný podľa uhlopriečky AC. Dĺžka AC je 12 cm, dĺžka BC je 6 cm a vnútorný uhol pri vrchole B je pravý. na stranách AB, AD sú dané body E, F tak, že trojuholník ECF je rovnostranný. Určite dĺžku úsečky EF.
Štvoruholník ABCD je súmerný podľa uhlopriečky AC. Dĺžka AC je 12 cm, dĺžka BC je 6 cm a vnútorný uhol pri vrchole B je pravý. na stranách AB, AD sú dané body E, F tak, že trojuholník ECF je rovnostranný. Určite dĺžku úsečky EF.
- Určte 21
 Určte vzdialenosť dvoch neprístupných miest K, L, ak sa z bodov A, B, ktoré sú od seba vzdialené 870 m, namerali veľkosti uhlov KAL=62°10", LAB= 41°23", KBL=66°34", LBA= 34°52". Ďakujem.
Určte vzdialenosť dvoch neprístupných miest K, L, ak sa z bodov A, B, ktoré sú od seba vzdialené 870 m, namerali veľkosti uhlov KAL=62°10", LAB= 41°23", KBL=66°34", LBA= 34°52". Ďakujem. - Objem 40
 Objem kvádra so štvorcovou podstavovou je 64 cm³ a odchýlka telesovej uhlopriečky od roviny podstavy je 45 stupňov. Vypočítajte jeho povrch.
Objem kvádra so štvorcovou podstavovou je 64 cm³ a odchýlka telesovej uhlopriečky od roviny podstavy je 45 stupňov. Vypočítajte jeho povrch. - Najväčší
 Vypočítajte najväčší uhol trojuholníku o stranách 158, 315, 453.
Vypočítajte najväčší uhol trojuholníku o stranách 158, 315, 453. - Výška 2
 Vypočítajte výšku rovnostranného trojuholníka so stranou 29.
Vypočítajte výšku rovnostranného trojuholníka so stranou 29. - Lanovka
 Určite výškový rozdiel lanovky keď stúpa o 67 promile a dĺžka lana je 930 m.
Určite výškový rozdiel lanovky keď stúpa o 67 promile a dĺžka lana je 930 m.
- Strana c
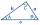 V △ABC a =3, b=6 a ∠ C = 110°. Vypočítajte dĺžku strany c.
V △ABC a =3, b=6 a ∠ C = 110°. Vypočítajte dĺžku strany c. - Zistite 4
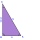 Zistite, či trojuholník ABC (s pravým uhlom pri vrchole C) je pravouhlý, ak: a) a= 3dm, b=40cm, c=0,5m b) a= 8dm, b=1,2m, c=6dm
Zistite, či trojuholník ABC (s pravým uhlom pri vrchole C) je pravouhlý, ak: a) a= 3dm, b=40cm, c=0,5m b) a= 8dm, b=1,2m, c=6dm - Kosodĺžnik
 Vypočítajte obsah a výšku krycej dosky tvaru kosodĺžnika, pre ktorý platí: d(BC)= 60 cm, uhol BAD = 45°, uhol ADB = 90°.
Vypočítajte obsah a výšku krycej dosky tvaru kosodĺžnika, pre ktorý platí: d(BC)= 60 cm, uhol BAD = 45°, uhol ADB = 90°. - Uhlopriečky
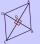 V kosoštvorcami je dané a = 160 cm, alfa = 60 stupňov. Vypočítajte veľkosti uhlopriečok.
V kosoštvorcami je dané a = 160 cm, alfa = 60 stupňov. Vypočítajte veľkosti uhlopriečok. - Rovnoramenný 19393
 Koľko dm² plochy zaberá rovnoramenný trojuholník, ak uhol pri základni má veľkosť 45˚ a základňa má dĺžku 10 cm.
Koľko dm² plochy zaberá rovnoramenný trojuholník, ak uhol pri základni má veľkosť 45˚ a základňa má dĺžku 10 cm.
Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať.
