MO B 2019 ukol 2
Přirozené číslo n má aspoň 73 dvojmístných dělitelů. Dokažte, že jedním z nich je číslo 60. Uveďte rovněž příklad čísla n, které má právě 73 dvojmístných dělitelů, včetně náležitého zdůvodnění.
Správná odpověď:

Zobrazuji 5 komentářů:
Dr Math
takto, 60 = 4 * 3 * 5
vypíšeme si dvouciferně cisla ktere nejsou dělitelné 5. Je jich 72. podezřelé číslo. V mnozine těchto 72 čísel su zarucene cisla ktere jsou dělitelné číslem 3 i 4. Tedy pokud k těmto 72 číslům pridam jakékoliv dvouciferně cislo, je zaručené dělitelem 5 (protože jsem vynechal jen dělitelné pěti). Pokud bych násobek všech 73 čísel, zarucene mam že výsledek násobení bude dělitelný 3,4 i 5, a proto i 60.
vypíšeme si dvouciferně cisla ktere nejsou dělitelné 5. Je jich 72. podezřelé číslo. V mnozine těchto 72 čísel su zarucene cisla ktere jsou dělitelné číslem 3 i 4. Tedy pokud k těmto 72 číslům pridam jakékoliv dvouciferně cislo, je zaručené dělitelem 5 (protože jsem vynechal jen dělitelné pěti). Pokud bych násobek všech 73 čísel, zarucene mam že výsledek násobení bude dělitelný 3,4 i 5, a proto i 60.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Trojúhelníku 40701
 V trojúhelníku ABC je bod S středem vepsané kružnice. Obsah čtyřúhelníku ABCS je roven čtyřem pětinám obsahu trojúhelníku ABC. Délky stran trojúhelníku ABC vyjádřené v centimetrech jsou všechny celočíselné a obvod trojúhelníku ABC je 15 cm. Určete délky s
V trojúhelníku ABC je bod S středem vepsané kružnice. Obsah čtyřúhelníku ABCS je roven čtyřem pětinám obsahu trojúhelníku ABC. Délky stran trojúhelníku ABC vyjádřené v centimetrech jsou všechny celočíselné a obvod trojúhelníku ABC je 15 cm. Určete délky s - Ovce 3
 Kuba se domluvil s bačou, že se mu bude starat o ovce. Bača Kubovi slíbil, že po roce služby dostane dvacet zlatých a k tomu jednu ovci. Jenže Kuba dal výpověď, právě když uplynul sedmý měsíc služby. I tak ho Bača spravedlivě odměnil a zaplatil mu pět zla
Kuba se domluvil s bačou, že se mu bude starat o ovce. Bača Kubovi slíbil, že po roce služby dostane dvacet zlatých a k tomu jednu ovci. Jenže Kuba dal výpověď, právě když uplynul sedmý měsíc služby. I tak ho Bača spravedlivě odměnil a zaplatil mu pět zla - Z6–I–5 MO 2019
 Útvar na obrázku vznikl tak, že z velkého kříže byl vystřižen malý kříž. Každý z těchto křížů může být složen z pěti shodných čtverců, přičemž strany malých čtverců jsou poloviční vzhledem ke stranám velkých čtverců. Obsah šedého útvaru na obrázku je 45 c
Útvar na obrázku vznikl tak, že z velkého kříže byl vystřižen malý kříž. Každý z těchto křížů může být složen z pěti shodných čtverců, přičemž strany malých čtverců jsou poloviční vzhledem ke stranám velkých čtverců. Obsah šedého útvaru na obrázku je 45 c - Z9–I–3 MO 2019
 Pro která celá čísla x je podíl (x+11)/(x+7) celým číslem? Najděte všechna řešení.
Pro která celá čísla x je podíl (x+11)/(x+7) celým číslem? Najděte všechna řešení.
- Z6-I-6 MO 2018
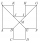 Ve dvanáctiúhelníku ABCDEF GHIJKL jsou každé dvě sousední strany kolmé a všechny strany s výjimkou stran AL a GF jsou navzájem shodné. Strany AL a GF jsou oproti ostatním stranám dvojnásobně dlouhé. Úsečky BG a EL se protínají v bodě M a rozdělují dvanáct
Ve dvanáctiúhelníku ABCDEF GHIJKL jsou každé dvě sousední strany kolmé a všechny strany s výjimkou stran AL a GF jsou navzájem shodné. Strany AL a GF jsou oproti ostatním stranám dvojnásobně dlouhé. Úsečky BG a EL se protínají v bodě M a rozdělují dvanáct - Z7–I–2 MO 2018
 Ve dvanáctiúhelníku ABCDEF GHIJKL jsou každé dvě sousední strany kolmé a všechny strany s výjimkou stran AL a GF jsou navzájem shodné. Strany AL a GF jsou oproti ostatním stranám dvojnásobně dlouhé. Úsečky BG a EL se protínají v bodě M. Čtyřúhelník ABMJ m
Ve dvanáctiúhelníku ABCDEF GHIJKL jsou každé dvě sousední strany kolmé a všechny strany s výjimkou stran AL a GF jsou navzájem shodné. Strany AL a GF jsou oproti ostatním stranám dvojnásobně dlouhé. Úsečky BG a EL se protínají v bodě M. Čtyřúhelník ABMJ m - MO Z8–I–5 - 2018
 Král dal zedníku Václavovi za úkol postavit zeď silnou 25 cm, dlouhou 50 m a vysokou 2 m. Pokud by Václav pracoval bez přestávky a stejným tempem, postavil by zeď za 26 hodin. Podle platných královských nařízení však musí Václav dodržovat následující podm
Král dal zedníku Václavovi za úkol postavit zeď silnou 25 cm, dlouhou 50 m a vysokou 2 m. Pokud by Václav pracoval bez přestávky a stejným tempem, postavil by zeď za 26 hodin. Podle platných královských nařízení však musí Václav dodržovat následující podm - Z7-1-3 MO 2018
 Děda připravil pro svých šest vnoučat hromádku lískových oříšků s tím, ať si je nějak rozeberou. První přišel Adam, odpočítal si polovinu, přibral si ještě jeden oříšek a odešel. Stejně se zachoval druhý Bob, třetí Cyril, čtvrtý Dan i pátý Eda. Jen Franta
Děda připravil pro svých šest vnoučat hromádku lískových oříšků s tím, ať si je nějak rozeberou. První přišel Adam, odpočítal si polovinu, přibral si ještě jeden oříšek a odešel. Stejně se zachoval druhý Bob, třetí Cyril, čtvrtý Dan i pátý Eda. Jen Franta - Z9-I-4 2018 Hoteliér
 Hoteliér chtěl vybavit jídelnu novými židlemi. V katalogu si vybral typ židle. Až při zadávání objednávky se od výrobce dozvěděl, že v rámci slevové akce nabízejí každou čtvrtou židli za poloviční cenu a že tedy oproti plánu může ušetřit za sedm a půl žid
Hoteliér chtěl vybavit jídelnu novými židlemi. V katalogu si vybral typ židle. Až při zadávání objednávky se od výrobce dozvěděl, že v rámci slevové akce nabízejí každou čtvrtou židli za poloviční cenu a že tedy oproti plánu může ušetřit za sedm a půl žid
- Z9 – I – 2 MO 2018
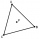 V rovnostranném trojúhelníku ABC je K středem strany AB, bod L leží v třetině strany BC blíže bodu C a bod M leží v třetině strany AC blíže bodu A. Určete, jakou část obsahu trojúhelníku ABC zabírá trojúhelník KLM.
V rovnostranném trojúhelníku ABC je K středem strany AB, bod L leží v třetině strany BC blíže bodu C a bod M leží v třetině strany AC blíže bodu A. Určete, jakou část obsahu trojúhelníku ABC zabírá trojúhelník KLM. - Bonbóny MO Z6-I-5 2017
 V plechovce byly červené a zelené bonbóny. Čeněk snědl 2/5 všech červených bonbónů a Zuzka snědla 3/5 všech zelených bonbónů. Teď tvoří červené bonbóny 3/8 všech bonbónů v plechovce. Kolik nejméně bonbónů mohlo být původně v plechovce?
V plechovce byly červené a zelené bonbóny. Čeněk snědl 2/5 všech červených bonbónů a Zuzka snědla 3/5 všech zelených bonbónů. Teď tvoří červené bonbóny 3/8 všech bonbónů v plechovce. Kolik nejméně bonbónů mohlo být původně v plechovce? - Sladkosti
 Anička má 50 Kč , Anežka má 46 Kč a za všechny peníze chtějí koupit zákusky na rodinou oslavu. Rozhodují se mezi dortíky a větrníky . Větrnik je o 4 Kč dražší než dortík a dortíků by se dalo za všechny peníze koupit o třetinu více než větrníků. Kolik stoj
Anička má 50 Kč , Anežka má 46 Kč a za všechny peníze chtějí koupit zákusky na rodinou oslavu. Rozhodují se mezi dortíky a větrníky . Větrnik je o 4 Kč dražší než dortík a dortíků by se dalo za všechny peníze koupit o třetinu více než větrníků. Kolik stoj - Mnohonožka Z6–I–3
 Mnohonožka Mirka sestává z hlavy a několika článků, na každém článku má jeden pár nohou. Když se ochladilo, rozhodla se, že se obleče. proto si na třetím článku od konce a potom na každém dalším třetím článku oblékla ponožku na levou nožku. Podobně si na
Mnohonožka Mirka sestává z hlavy a několika článků, na každém článku má jeden pár nohou. Když se ochladilo, rozhodla se, že se obleče. proto si na třetím článku od konce a potom na každém dalším třetím článku oblékla ponožku na levou nožku. Podobně si na - Polévka
 V pondělí uvařili 25 hrnců a 10 kotlů polévky. V úterý 15 hrnců a 13 kotlů. Ve středu 20 hrnců a ve čtvrtek 30 kotlů. V pondělí a úterý uvařili stejné množství polévky. Kolikrát více polévky uvařili ve čtvrtek jako ve středu?
V pondělí uvařili 25 hrnců a 10 kotlů polévky. V úterý 15 hrnců a 13 kotlů. Ve středu 20 hrnců a ve čtvrtek 30 kotlů. V pondělí a úterý uvařili stejné množství polévky. Kolikrát více polévky uvařili ve čtvrtek jako ve středu?
- Pastevci
 Na louce se pasou koně, krávy a ovce, spolu jich je méně než 200. Kdyby bylo krav 45-krát více, koní 60-krát více a ovcí 35krát více než jejich je nyní, jejich počty by se rovnaly. Kolik se spolu na louce pase koní, krav a ovcí?
Na louce se pasou koně, krávy a ovce, spolu jich je méně než 200. Kdyby bylo krav 45-krát více, koní 60-krát více a ovcí 35krát více než jejich je nyní, jejich počty by se rovnaly. Kolik se spolu na louce pase koní, krav a ovcí? - Vzdálenost 145
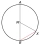 Vzdálenost tětivy od středu je 6 cm. Středový úhel je 60°. Vypočítejte plošný obsah kruhové úseče.
Vzdálenost tětivy od středu je 6 cm. Středový úhel je 60°. Vypočítejte plošný obsah kruhové úseče. - Rovnice 47
 Rovnice se zlomkama: 3y - y+3/4 = 1+y/2
Rovnice se zlomkama: 3y - y+3/4 = 1+y/2
