Dotyčnice

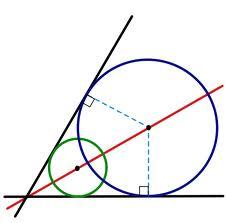
Ku kružnici s polomerom 106 dm sú z bodu S vedené dve dotyčnice. Vzdialenosť obidvoch dotykových bodov je 102 dm.
Vypočítajte vzdialenosť bodu S od stredu kružnice.

Správna odpoveď:

d =  120,9 dm

Postup správneho riešenia:

$$\begin{gathered} 106^2=c_1(c_1+c_2) \\ {\displaystyle \frac{102^2}{4}}=c_2{c}_1 \\ 106^2=c_1^2+{\displaystyle \frac{102^2}{4}} \\ {c}_1=\sqrt{106^2-{\displaystyle \frac{102^2}{4}}}=92.925dm \\ {c}_2={\displaystyle \frac{102^2}{4}}\mathrm{/}{c}_1=27.99dm \\ d=c_1+c_2=120.9\text{ dm} \end{gathered}$$

Skúsiť iný príklad

Súvisiace a podobné príklady:

• Ku kružnici
  Ku kružnici s polomerom 76 mm sú z bodu C vedené dve dotyčnice. Vzdialenosť obidvoch dotykových bodov je 14 mm. Vypočítajte vzdialenosť bodu C od stredu kružnice.
• Bod dotyku
  Bod A má od kružnice s polomerom r = 4cm a stredom S vzdialenosť IA, kl = 10 cm. Vypočítajte: a) vzdialenosť bodu A od bodu dotyku T, ak je dotyčnica ku kružnici vedená z bodu A b) vzdialenosť dotykového bodu T od spojnice SA
• Tetiva 2
  Bod A má od stredu kružnice s polomerom r = 5 cm vzdialenosť 13 cm. Vypočítajte dĺžku tetivy spájajúca body dotyku T1 a T2 dotyčníc vedených z bodu A ku kružnici k.
• Kružnice
  V kružnici s polomerom 7,5 cm sú zostrojené 2 rovnobežné tetivy, ktorých dĺžky sú 9 cm a 12 cm. Vypočítajte vzdialenosť týchto tetív (ak sú možné dve riešenia napíšte obe).
• Tetiva
  Akú dĺžku x má tetiva kružnice s priemerom 60 m, ak je vzdialená od stredu kružnice 10 m?
• V kružnici 2
  V kružnici s priemerom 70 cm sú narysované dve rovnobežné tetivy tak, že stred kružnice leží medzi tetivami. Vypočítaj vzdialenosť týchto tetív, ak jedna z nich má dĺžku 42 cm a druhá 56 cm.
• Dve tetivy
  V kružnici sú vedené dve tetivy dlhé 30 a 34 cm. Kratšia z nich je od stredu dvakrát ďalej než dlhšia. Urči polomer kružnice.
• Kosoštvorec a vpísaná
  Kosoštvorec má stranu a = 6 cm, polomer vpísanej kružnice je r = 2 cm. Vypočítajte dĺžky oboch uhlopriečok.
• Tetiva
  Akú dĺžku má tetiva AB, ktorej vzdialenosť od stredu S kružnice k(S, 92 cm) sa rovná 10 cm?
• PT strany
  Vypočítajte strany pravouhlého trojuholníka, ak je zadaná, že a + b = 17cm, polomer vpísanej kružnice ρ = 2cm.
• Tetiva
  V kružnici s polomerom 10 cm je 12 cm dlhá tetiva. Vypočítaj vzdialenosť tetivy od stredu kružnice.
• Tetiva
  V kružnici k (S; 6cm) vypočítajte vzdialenosť tetivy t od stredu kružnice S, ak dĺžka tetivy je t= 10cm.
• Obsah kruhu
  Vypočítajte obsah kruhu, ktorý má rovnaký obvod ako je obvod obdĺžnika vpísanej kružnici s polomerom r 9 cm tak, že jeho strany sú v pomere 2 ku 7.
• Tetivy pod uhlom
  Z bodu na kružnici s priemerom 8 cm sú vedené dve zhodné tetivy, ktoré zvierajú uhol 60°. Vypočítaj dĺžku týchto tetív.
• Tetivy
  V kružnici s polomerom 8,5 cm sú zostrojené dve rovnobežné tetivy, ktorých dĺžky sú 9 cm a 12 cm. Vypočítajte vzdialenosť tetív v kružnici.
• Štvrťkruh 4
  Aký polomer má kruh vpisany do štvrťkruhu s polomerom 100 cm?
• Tetiva 5
  Vypočítajte dĺžku tetivy kružnice s polomerom r = 10 cm, ktorej dĺžka sa rovná jej vzdialenosti od stredu kružnice.