MO-Z6-I-2 2017
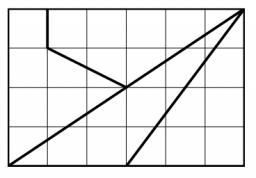
Erika chcela ponúknuť čokoládu svojim trom kamarátkam. Keď ju vytiahla z batohu, zistila, že je polámaná ako na obrázku. (Vyznačené štvorčeky sú navzájom zhodné. ) Dievčatá sa dohodli, že čokoládu ďalej lámať nebudú a lósom určia, aký veľký kúsok ktorá dostane. Zoraďte štyri kúsky čokolády odnajmenšieho po najväčší.
Správna odpoveď:
Zobrazujem 5 komentárov:
Dr Math
S1 = je obsah trojuholnika vpravo dole, zakladna 3 , vyska 4....
S2 = je obsah trojuholnika vlavo dole, opat zakladna 3 a vyska 4...
S3 je obsah 4 uholnika vpravo hore co vyzera takmer ako trojuholnik. Sklada sa z odcitnia obsahov dvoch trojuholnikov.
a) trojuholnika o zakladni 7 a vysky 2. Zakladna 7 (obdlznik ma dlhsiu stranu len 6) preto lebo predlzenie ciary smerujuce vlavo hore pretne predlzenu stranu obdlznika, tak ze zformuje trojuholnik o zakladni 7.... tj. o jeden dielik vlavo od horneho laveho vrcholu obdlznika. Inymi slovami ciara smerujuca vlavo hore, iduca v sklone 1 dielik vertikalne ku 2 horizontalne pretne predlzenu stranu obdlznika az 1 dielik od vrcholu.
b) a musime odcitat obsah pravouhleho trojuholnika o odvesne 1 a druhej odvesne 2.
S4 je obsah obdlznika minus S1+S2+S3 (zvysna plocha)
S2 = je obsah trojuholnika vlavo dole, opat zakladna 3 a vyska 4...
S3 je obsah 4 uholnika vpravo hore co vyzera takmer ako trojuholnik. Sklada sa z odcitnia obsahov dvoch trojuholnikov.
a) trojuholnika o zakladni 7 a vysky 2. Zakladna 7 (obdlznik ma dlhsiu stranu len 6) preto lebo predlzenie ciary smerujuce vlavo hore pretne predlzenu stranu obdlznika, tak ze zformuje trojuholnik o zakladni 7.... tj. o jeden dielik vlavo od horneho laveho vrcholu obdlznika. Inymi slovami ciara smerujuca vlavo hore, iduca v sklone 1 dielik vertikalne ku 2 horizontalne pretne predlzenu stranu obdlznika az 1 dielik od vrcholu.
b) a musime odcitat obsah pravouhleho trojuholnika o odvesne 1 a druhej odvesne 2.
S4 je obsah obdlznika minus S1+S2+S3 (zvysna plocha)
6 rokov 3 Likes
Tipy na súvisiace online kalkulačky
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Téma:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Čokoláda
 Tabuľka čokolády je náznakovo rozdelená na štvorčeky. Po dĺžke je na nej 15 štvorčekov a po šírke 19 štvorčekov. Čokoládu ideme rozlámať na jednotlivé štvorčeky. Koľkokrát ju musíme rozlomiť, aby zostali už iba jednotlivé štvorčeky? Nedovoľuje sa lámať vi
Tabuľka čokolády je náznakovo rozdelená na štvorčeky. Po dĺžke je na nej 15 štvorčekov a po šírke 19 štvorčekov. Čokoládu ideme rozlámať na jednotlivé štvorčeky. Koľkokrát ju musíme rozlomiť, aby zostali už iba jednotlivé štvorčeky? Nedovoľuje sa lámať vi - Určte 12
 Určte koľko kúskov štvorčekov mala čokoláda, ak by sme ju po rozdelení na najmenšie kúsky štvorčeky rozdelili bezo zvyšku medzi piatich aj troch ľudí spravodlivo každému človeku rovnaký diel.
Určte koľko kúskov štvorčekov mala čokoláda, ak by sme ju po rozdelení na najmenšie kúsky štvorčeky rozdelili bezo zvyšku medzi piatich aj troch ľudí spravodlivo každému človeku rovnaký diel. - Julka
 Julka si chcela zo špagáta dlhého 1 m nastrihať kúsky dlhé 10 cm a 30 cm tak, aby jej nezvýšil ani kúsok. Podarilo sa jej to?
Julka si chcela zo špagáta dlhého 1 m nastrihať kúsky dlhé 10 cm a 30 cm tak, aby jej nezvýšil ani kúsok. Podarilo sa jej to? - Adam mal 3
 Adam mal papier, ktorý bol natoľko veľký, že by sa z neho dalo natrhať niekoľko desiatok tisíc kúskov. Najprv papier roztrhal na štyri kúsky. Každý z týchto kú skov vzal a roztrhal buď na štyri, alebo na desať kúskov. Rovnakým spôsobom pokračo
Adam mal papier, ktorý bol natoľko veľký, že by sa z neho dalo natrhať niekoľko desiatok tisíc kúskov. Najprv papier roztrhal na štyri kúsky. Každý z týchto kú skov vzal a roztrhal buď na štyri, alebo na desať kúskov. Rovnakým spôsobom pokračo
- Spravodlivo 3989
 Koľko cukríkov má Renata v bonboniére? Je ich menej ako 50, môže ich rozdeliť spravodlivo svojim piatim poprípade aj šiestim kamarátkam a ešte na ňu a jej bračeka po jednom cukríku zostane. Koľko je v cukríku cukríkov?
Koľko cukríkov má Renata v bonboniére? Je ich menej ako 50, môže ich rozdeliť spravodlivo svojim piatim poprípade aj šiestim kamarátkam a ešte na ňu a jej bračeka po jednom cukríku zostane. Koľko je v cukríku cukríkov? - Čokoláda 6
 Medzinárodná banda pašerákov čokolády vedená slávnym Jackom Krivým Nosom, ktorý má 7 spolupracovníkov, si vytipovalal bratislavské letisko ako križovatku svojich obchodov. Lietadlo z Bratislavy do Štokholmu lieta každý tretí deň. Lietadlo z Bratislavy do
Medzinárodná banda pašerákov čokolády vedená slávnym Jackom Krivým Nosom, ktorý má 7 spolupracovníkov, si vytipovalal bratislavské letisko ako križovatku svojich obchodov. Lietadlo z Bratislavy do Štokholmu lieta každý tretí deň. Lietadlo z Bratislavy do - Odkloniť o uhol
 Cyklista prechádza zákrutou s polomerom 20 m rýchlosťou 25 km/h. O aký veľký uhol sa musí odkloniť od zvislého smeru dovnútra zákruty?
Cyklista prechádza zákrutou s polomerom 20 m rýchlosťou 25 km/h. O aký veľký uhol sa musí odkloniť od zvislého smeru dovnútra zákruty? - Čokoláda
 Koľkokrát treba rozlomiť čokoládu zloženú z 8 × 10 dielov, aby sme dostali 80 dielov?
Koľkokrát treba rozlomiť čokoládu zloženú z 8 × 10 dielov, aby sme dostali 80 dielov? - Aká je 4
 Aká je pravdepodobnosť že v rodine so 4 deťmi sú po a) aspoň 3 dievčatá b) aspoň 1 chlapec keď pravdepodobnosť narodenia chlapca je 0,51
Aká je pravdepodobnosť že v rodine so 4 deťmi sú po a) aspoň 3 dievčatá b) aspoň 1 chlapec keď pravdepodobnosť narodenia chlapca je 0,51
- Kráľ rozdelil
 Kráľ rozdelil dedičstvo svojim trom synom v pomere 7:6:4. Dvaja z nich dostali spolu 286000 zlatých. Koľko dostal každý zo synov.
Kráľ rozdelil dedičstvo svojim trom synom v pomere 7:6:4. Dvaja z nich dostali spolu 286000 zlatých. Koľko dostal každý zo synov. - Predpokladal 82129
 Mamička kúpila svojim trom deťom košík marhúľ s odkazom, nech sa spravodlivo rozdelí. Ráno si z košíka vzala spravodlivo Jitka 1/3, na poludnie prišiel Martin a vzal si aj 1/3. Ako posledná prišla ku košíku Pavla, poslúchla odkaz mamičky a vzala si 4 marh
Mamička kúpila svojim trom deťom košík marhúľ s odkazom, nech sa spravodlivo rozdelí. Ráno si z košíka vzala spravodlivo Jitka 1/3, na poludnie prišiel Martin a vzal si aj 1/3. Ako posledná prišla ku košíku Pavla, poslúchla odkaz mamičky a vzala si 4 marh - Do kina
 Janka sa v 8 hod dozvedela, že všetkých 1093 žiakov školy pôjde do kina. Počas 20 min. to povedala 3 kamarátom. Každý z nich to opäť za 20 min. povedal ďalším trom. Týmto spôsobom sa správa šírila ďalej. V koľko hodín sa ju dozvedeli všetky deti v škole?
Janka sa v 8 hod dozvedela, že všetkých 1093 žiakov školy pôjde do kina. Počas 20 min. to povedala 3 kamarátom. Každý z nich to opäť za 20 min. povedal ďalším trom. Týmto spôsobom sa správa šírila ďalej. V koľko hodín sa ju dozvedeli všetky deti v škole? - Hanka
 Hanka strihala slamky dlhé 20 cm na tri kúsky každý kúsok mal dlžku v cm. Potom s týchto troch kúskov skušala zložiť trojuholník. a) Aký obvod mal každý z trojuholníkov? b) Koľko môže merať najdlhšia strana? c) Koľko rôznych trojuholníkov mohla poskladať?
Hanka strihala slamky dlhé 20 cm na tri kúsky každý kúsok mal dlžku v cm. Potom s týchto troch kúskov skušala zložiť trojuholník. a) Aký obvod mal každý z trojuholníkov? b) Koľko môže merať najdlhšia strana? c) Koľko rôznych trojuholníkov mohla poskladať? - Narysujte: 2511
 Narysujte kružnicu k/S 4,5 cm/. Ďalej narysujte: a/dva navzájom kolmé priemery AB a CD b/dva polomery SA a SE, ktoré zvierajú uhol 75 stupňov c/tetiva /KL/= 4 cm d/tetiva /MN/, ktorá je kolmá ku KL
Narysujte kružnicu k/S 4,5 cm/. Ďalej narysujte: a/dva navzájom kolmé priemery AB a CD b/dva polomery SA a SE, ktoré zvierajú uhol 75 stupňov c/tetiva /KL/= 4 cm d/tetiva /MN/, ktorá je kolmá ku KL
- Včelár
 Starý otec je včelár a chce rozdeliť svojim trom vnukom med. Má sedem rovnakých nádob plných medu, sedem nádob naplnených do polovice a sedem prázdnych nádob. Ako má nádoby rozdeliť (bez prelievania) medzi vnukov, aby každý dostal rovnaký počet nádob aj r
Starý otec je včelár a chce rozdeliť svojim trom vnukom med. Má sedem rovnakých nádob plných medu, sedem nádob naplnených do polovice a sedem prázdnych nádob. Ako má nádoby rozdeliť (bez prelievania) medzi vnukov, aby každý dostal rovnaký počet nádob aj r - Sladkosti 39531
 Triedna učiteľka kúpila na konci roka svojim žiakom hrnček a sladkosti. Jeden hrnček stál 15 Sk, čokoláda 12 Sk a oblátku 9 Sk. Chalani dostali hrnček a čokoládu, dievčatá hrnček a oblátku. Koľko korún pani učiteľka zaplatila, ak chlapcov bolo v triede x
Triedna učiteľka kúpila na konci roka svojim žiakom hrnček a sladkosti. Jeden hrnček stál 15 Sk, čokoláda 12 Sk a oblátku 9 Sk. Chalani dostali hrnček a čokoládu, dievčatá hrnček a oblátku. Koľko korún pani učiteľka zaplatila, ak chlapcov bolo v triede x - KLMN
 V lichobežníku KLMN platí že, strany KL a MN sú rovnobežné, úsečky KL a KM sú zhodné, úsečky KN, NM a ML sú navzájom zhodné. Určte veľkosť uhla KMN.
V lichobežníku KLMN platí že, strany KL a MN sú rovnobežné, úsečky KL a KM sú zhodné, úsečky KN, NM a ML sú navzájom zhodné. Určte veľkosť uhla KMN.
