Loď
Sila 300 kg (3000 N) je nutná na vytiahnutie lode po rampe so sklonom 14° zvierajúcom s vodorovnou rovinou.
Koľko váži loď?
Koľko váži loď?
Správna odpoveď:

Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- geometria
- podobnosť trojuholníkov
- planimetria
- pravouhlý trojuholník
- trojuholník
- goniometria a trigonometria
- sínus
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Rýchlosťou 7004
 Po palube lodí kráča lodník stálou rýchlosťou 5 km/h v smere, ktorý zviera so smerom rýchlosti lode uhol 60°. Loď sa pohybuje vzhľadom na pokojnú hladinu jazera stálou rýchlosťou 10 km/h. Určite graficky veľkosť rýchlosti, ktorou sa lodník pohybuje vzhľad
Po palube lodí kráča lodník stálou rýchlosťou 5 km/h v smere, ktorý zviera so smerom rýchlosti lode uhol 60°. Loď sa pohybuje vzhľadom na pokojnú hladinu jazera stálou rýchlosťou 10 km/h. Určite graficky veľkosť rýchlosti, ktorou sa lodník pohybuje vzhľad - Teleso, trenie
 Teleso sa šmýka dolu po naklonenej rovine zvierajúcej s vodorovnou rovinou uhol α=π/4=45° za účinku síl trenia so zrýchlením a = 2,4 m/s². Pod akým uhlom β musí byť naklonená rovina, aby sa teleso po nej šmýkalo po malom postrčení konštantnou rýchlosťou?
Teleso sa šmýka dolu po naklonenej rovine zvierajúcej s vodorovnou rovinou uhol α=π/4=45° za účinku síl trenia so zrýchlením a = 2,4 m/s². Pod akým uhlom β musí byť naklonená rovina, aby sa teleso po nej šmýkalo po malom postrčení konštantnou rýchlosťou? - Výška v PT
 Jedna strana pravoúhleho trojuholníka je dlhá 36 so sklonom 15°. Aká je výška na konci tejto strany?
Jedna strana pravoúhleho trojuholníka je dlhá 36 so sklonom 15°. Aká je výška na konci tejto strany? - Raketa
 Vystrelí sa raketa s rýchlosťou 100 fps (stôp za sekundu) v smere 30° nad vodorovnou rovinou. Určte maximálnu výšku, do ktorej stúpa? Fps je stopa za sekundu.
Vystrelí sa raketa s rýchlosťou 100 fps (stôp za sekundu) v smere 30° nad vodorovnou rovinou. Určte maximálnu výšku, do ktorej stúpa? Fps je stopa za sekundu.
- Navigácia lode
 Loď pláva 84 km na kurze 17° a potom cestuje na kurze 107° 135 km. Nájdite vzdialenosť konca cesty z východiskového bodu a zaokrúhlite na najbližší kilometer.
Loď pláva 84 km na kurze 17° a potom cestuje na kurze 107° 135 km. Nájdite vzdialenosť konca cesty z východiskového bodu a zaokrúhlite na najbližší kilometer. - Maják
 Z vrcholu majáku vo výške 145 stôp nad morom je hĺbkový uhol (uhol depresie) lode 29°. Ako ďaleko je loď od majáku?
Z vrcholu majáku vo výške 145 stôp nad morom je hĺbkový uhol (uhol depresie) lode 29°. Ako ďaleko je loď od majáku? - Rybárska loď
 Rybárska loď ulovila za jeden deň 14 rýb. Koľko rýb uloví dohromady 4 rybárske lode za 8 dní?
Rybárska loď ulovila za jeden deň 14 rýb. Koľko rýb uloví dohromady 4 rybárske lode za 8 dní? - Zvierajú 67664
 Sila R = 12 N sa má rozdeliť na dve zložky F1, F2, ich smery zvierajú so smerom sily R uhlami α = 30°, β = 45°. Aké sú zložky F1, F2?
Sila R = 12 N sa má rozdeliť na dve zložky F1, F2, ich smery zvierajú so smerom sily R uhlami α = 30°, β = 45°. Aké sú zložky F1, F2? - Dron
 Lietajúci dron zameriaval územie pre architekta. Vzlietol kolmo z bodu C do bodu D. Bol vo výške 300 m nad rovinou ABC. Dron z bodu D zameral uhol BDC 43°. Vypočítajte v metroch vzdialenosť bodov C a B.
Lietajúci dron zameriaval územie pre architekta. Vzlietol kolmo z bodu C do bodu D. Bol vo výške 300 m nad rovinou ABC. Dron z bodu D zameral uhol BDC 43°. Vypočítajte v metroch vzdialenosť bodov C a B.
- Ihlan 14
 Urči povrch pravidelného štvorbokého ihlana, keď je daný jeho objem V = 120 a uhol bočnej steny s rovinou podstavy je α = 42°30´.
Urči povrch pravidelného štvorbokého ihlana, keď je daný jeho objem V = 120 a uhol bočnej steny s rovinou podstavy je α = 42°30´. - Naklonená rovina
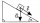 Teleso spočíva na naklonenej rovine a pôsobí na nej tlakovou silou s veľkosťou 70N. Určte aký uhol zviera naklonená rovina s horizontálnou rovinou ak na teleso pôsobí tiažová sila s veľkosťou 100N.
Teleso spočíva na naklonenej rovine a pôsobí na nej tlakovou silou s veľkosťou 70N. Určte aký uhol zviera naklonená rovina s horizontálnou rovinou ak na teleso pôsobí tiažová sila s veľkosťou 100N. - Sklon
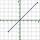 Aká je smernica priamky so sklonom -221°?
Aká je smernica priamky so sklonom -221°? - Lode
 1. Grécka loď odchádza o 6 a vezie kávu. 2. Prostredná loď má čierny komín. 3. Anglická loď odchádza o deviatej. 4. Francúzska loď je vľavo o lodi vezúcej kávu a má modrý komín . 5. Vpravo od lodi vezúcej kakao je loď idúca do Marseille, 6. Brazilska lod
1. Grécka loď odchádza o 6 a vezie kávu. 2. Prostredná loď má čierny komín. 3. Anglická loď odchádza o deviatej. 4. Francúzska loď je vľavo o lodi vezúcej kávu a má modrý komín . 5. Vpravo od lodi vezúcej kakao je loď idúca do Marseille, 6. Brazilska lod - Otrokoviciach 60903
 Zo Strážnice vycestovala po Baťovom kanáli motorová loď rýchlosťou 12 km/h smerom ku kotvisku pri Otrokoviciach. O dve hodiny neskôr sa za ňou vybrala druhá loď rýchlosťou 20 km/h. Do Otrokovíc prišli obe lode súčasne. Koľko kilometrov je to zo Strážnice
Zo Strážnice vycestovala po Baťovom kanáli motorová loď rýchlosťou 12 km/h smerom ku kotvisku pri Otrokoviciach. O dve hodiny neskôr sa za ňou vybrala druhá loď rýchlosťou 20 km/h. Do Otrokovíc prišli obe lode súčasne. Koľko kilometrov je to zo Strážnice
- Mimozemská loď
 Mimozemská loď má tvar gule o polomere r = 3000m a jej posádka potrebuje loďou odviezť nazbieraný výskumný materiál v boxe v tvare kvádra so štvorcovou podstavou. Určte dĺžku podstavy a (a výšku h) tak, aby mal box najväčší možný objem.
Mimozemská loď má tvar gule o polomere r = 3000m a jej posádka potrebuje loďou odviezť nazbieraný výskumný materiál v boxe v tvare kvádra so štvorcovou podstavou. Určte dĺžku podstavy a (a výšku h) tak, aby mal box najväčší možný objem. - Tri lode
 V prístave kotvia tri lode, ktoré spoločne vyplávajú. Prvý lod sa vracia po dvoch týždňoch, druhá po 4 týždňoch a tretia po 8 týždňoch. Za koľko týždňov sa prvýkrát zase lode stretnú v prístave a koľkokrát sa, ktorá z lodí medzitým v prístave objavila-nep
V prístave kotvia tri lode, ktoré spoločne vyplávajú. Prvý lod sa vracia po dvoch týždňoch, druhá po 4 týždňoch a tretia po 8 týždňoch. Za koľko týždňov sa prvýkrát zase lode stretnú v prístave a koľkokrát sa, ktorá z lodí medzitým v prístave objavila-nep - O koľko 14
 O koľko °C sa zmení teplota železného kľúča s hmotnosťou 0,004 t, ak prijme teplo 360 000 J? ( c železa je 450 J/kg .°C )
O koľko °C sa zmení teplota železného kľúča s hmotnosťou 0,004 t, ak prijme teplo 360 000 J? ( c železa je 450 J/kg .°C )
