Pětiboký jehlan
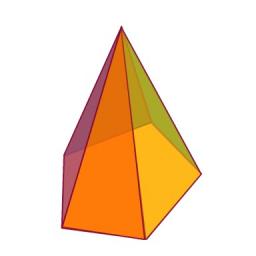
Vypočtěte objem pravidelného 5-bokého jehlanu ABCDEV, pokud |AB| = 7,7 cm a roviny ABV, ABC svírají úhel 37 stupňů.
Správná odpověď:
Zobrazuji 3 komentáře:
Žák
Použití spojovníku mezi číslovkou a slovem je nevhodné. Správné 5boký, ještě správnější pětiboký.
Tipy na související online kalkulačky
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- stereometrie
- jehlan
- planimetrie
- pravoúhlý trojúhelník
- mnohoúhelník
- trojúhelník
- goniometrie a trigonometrie
- tangens
Jednotky fyzikálních veličin:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Spádnice
 Určit objem a povrch kužele, jehož spádnice o délce 8cm svírá s rovinou podstavy úhel 75 stupňů
Určit objem a povrch kužele, jehož spádnice o délce 8cm svírá s rovinou podstavy úhel 75 stupňů - Hranol RRPT
 Vypočítejte objem a povrch hranolu o výšce 120mm, jehož podstavce je rovnoramenný trojúhelník s odvěsnou dlouhou 5cm.
Vypočítejte objem a povrch hranolu o výšce 120mm, jehož podstavce je rovnoramenný trojúhelník s odvěsnou dlouhou 5cm. - Kužel
 Kužel měří na základně průměr 6 palců. Vzdálenost od okraje obvodu k vrcholu je 12 palců. Najděte jeho objem. (palec=inch)
Kužel měří na základně průměr 6 palců. Vzdálenost od okraje obvodu k vrcholu je 12 palců. Najděte jeho objem. (palec=inch) - Urči poloměr RS kužela
 Urči poloměr a výšku (v centimetrech) rovnostranného kúželu, který má objem 1 litr
Urči poloměr a výšku (v centimetrech) rovnostranného kúželu, který má objem 1 litr
- Vypočítejte
 Vypočítejte hmotnost dřevěného pravidelného trojbokého hranolu s výškou rovnající se obvodu podstavy a postavou vepsanou do kružnice o poloměru 6, M cm, kde M je měsíc vašeho narození. Hustota dubu je 680 kg/m³.
Vypočítejte hmotnost dřevěného pravidelného trojbokého hranolu s výškou rovnající se obvodu podstavy a postavou vepsanou do kružnice o poloměru 6, M cm, kde M je měsíc vašeho narození. Hustota dubu je 680 kg/m³. - 3S hranol
 Najděte objem a povrch trojúhelníkového hranolu s pravoúhlým trojúhelníkovým dnem, pokud je délka odvěsen dna hranolu je 7,2 cm a 4,7 cm a výška hranolu je 24 cm.
Najděte objem a povrch trojúhelníkového hranolu s pravoúhlým trojúhelníkovým dnem, pokud je délka odvěsen dna hranolu je 7,2 cm a 4,7 cm a výška hranolu je 24 cm. - Čtvercovou 44061
 Jehlanová svíčka s čtvercovou podstavou má boční hranu s = 12 cm a hranu podstavy 4 cm. Kolik vosku budeme potřebovat k její výrobě a jak dlouhý knot, pokud je o 5% větší než její výška.
Jehlanová svíčka s čtvercovou podstavou má boční hranu s = 12 cm a hranu podstavy 4 cm. Kolik vosku budeme potřebovat k její výrobě a jak dlouhý knot, pokud je o 5% větší než její výška. - V trojúhelníku 10
 V trojúhelníku ABC se velikost vnějšího úhlu při vrcholu C rovná 126°. Velikost vnitřních úhlů při vrcholech A, B jsou v poměru 5: 9. Vypočítej velikost vnitřních úhlů α, β, γ trojúhelníku ABC.
V trojúhelníku ABC se velikost vnějšího úhlu při vrcholu C rovná 126°. Velikost vnitřních úhlů při vrcholech A, B jsou v poměru 5: 9. Vypočítej velikost vnitřních úhlů α, β, γ trojúhelníku ABC. - Čtyřúhelník ACEG
 Na obrázku jsou dva obdélníky ABCD a DEFG, přičemž |DE|=3 CM, |AD|=6 CM, |DG|= 5, |CD|= 10 CM. Vypočítejte obsah čtyřúhelníku ACEG. Popis obrázku: obdélníky mají společný jeden vrchol D. Obdélník ABCD má dvojnásobně dlouhé strany než DEFG. Všechny stranu
Na obrázku jsou dva obdélníky ABCD a DEFG, přičemž |DE|=3 CM, |AD|=6 CM, |DG|= 5, |CD|= 10 CM. Vypočítejte obsah čtyřúhelníku ACEG. Popis obrázku: obdélníky mají společný jeden vrchol D. Obdélník ABCD má dvojnásobně dlouhé strany než DEFG. Všechny stranu
- Trojuhelníku 135
 Trojuhelníku ABC o stranách a = 15 cm, b = 17,4 cm, c = 21,6 cm je opsána kružnice. Vypočítejte obsah úsečí určených stranami trojúhelníku.
Trojuhelníku ABC o stranách a = 15 cm, b = 17,4 cm, c = 21,6 cm je opsána kružnice. Vypočítejte obsah úsečí určených stranami trojúhelníku. - Pozorovatel 11
 Pozorovatel vidí letadlo pod výškovým úhlem 35° (úhel od vodorovné roviny). V tu chvíli letadlo hlásí výšku 4 km. Jak daleko od pozorovatele je místo, nad kterým letadlo letí. Zaokrouhli na stovky metrů.
Pozorovatel vidí letadlo pod výškovým úhlem 35° (úhel od vodorovné roviny). V tu chvíli letadlo hlásí výšku 4 km. Jak daleko od pozorovatele je místo, nad kterým letadlo letí. Zaokrouhli na stovky metrů. - Vzdálenost 145
 Vzdálenost tětivy od středu je 6 cm. Středový úhel je 60°. Vypočítejte plošný obsah kruhové úseče.
Vzdálenost tětivy od středu je 6 cm. Středový úhel je 60°. Vypočítejte plošný obsah kruhové úseče. - Kruh - úseč
 Kruh o průměru 30 cm je přeťat tětivou t = 16 cm. Vypočtěte obvod a obsah menší úseče.
Kruh o průměru 30 cm je přeťat tětivou t = 16 cm. Vypočtěte obvod a obsah menší úseče. - Těžítko 3
 Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³?
Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³?
- Trojúhelníku 83261
 Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3
Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3 - Štvobokého 83259
 Obvod štvobokého ihlava je 48 ma jeho výška je 2,5 m; kolik bude stát plech na tento jehlan, když 1m² stojí 1,5 €; do plochy se počítá i 12% ztráta na spoje a záhyby.
Obvod štvobokého ihlava je 48 ma jeho výška je 2,5 m; kolik bude stát plech na tento jehlan, když 1m² stojí 1,5 €; do plochy se počítá i 12% ztráta na spoje a záhyby. - Krychle 50
 Krychle ABCDEFGH má hranu délky 3 cm. Vypočítejte objem jehlanu ABCDH.
Krychle ABCDEFGH má hranu délky 3 cm. Vypočítejte objem jehlanu ABCDH.
