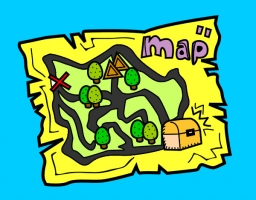
Na mapě 7
Určete měřítko mapy, je-li les tvaru trojúhelníku o rozměrech 1,6 km, 2,4 km a 2,7 km na mapě zakreslen jako trojúhelník o stranách délek 32 mm, 48 mm a 54 mm.
Správná odpověď:
Tipy na související online kalkulačky
Potřebujete pomoci sčítat, zkrátít či vynásobit zlomky? Zkuste naši zlomkovou kalkulačku.
Vyzkoušejte naši kalkulačka na přepočet poměru.
Chcete proměnit jednotku délky?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte naši kalkulačka na přepočet poměru.
Chcete proměnit jednotku délky?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Jednotky fyzikálních veličin:
Téma:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- V trojúhelníku 10
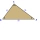 V trojúhelníku ABC se velikost vnějšího úhlu při vrcholu C rovná 126°. Velikost vnitřních úhlů při vrcholech A, B jsou v poměru 5: 9. Vypočítej velikost vnitřních úhlů α, β, γ trojúhelníku ABC.
V trojúhelníku ABC se velikost vnějšího úhlu při vrcholu C rovná 126°. Velikost vnitřních úhlů při vrcholech A, B jsou v poměru 5: 9. Vypočítej velikost vnitřních úhlů α, β, γ trojúhelníku ABC. - Z rozhledně
 Z rozhledně vysoké 40 m je vidět vrchol topolu pod hloubkovym uhlem o velikosti 50*10´a patu topolu v hloubkovem úhlu o velikosti 58*. Vypocitejte výšku topolu.
Z rozhledně vysoké 40 m je vidět vrchol topolu pod hloubkovym uhlem o velikosti 50*10´a patu topolu v hloubkovem úhlu o velikosti 58*. Vypocitejte výšku topolu. - Vypočítejte 82693
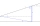 Vypočítejte výšku stožáru, jehož patu vidíme v hloubkovém úhlu 11° a vrchol ve výškovém úhlu 28°. Stožár je pozorován z místa 10 m nad úrovní paty stožáru.
Vypočítejte výšku stožáru, jehož patu vidíme v hloubkovém úhlu 11° a vrchol ve výškovém úhlu 28°. Stožár je pozorován z místa 10 m nad úrovní paty stožáru. - Školní 13
 Školní budova vrhá na rovinu dvora stín 16 m dlouhý a v téže době vrhá svislá metrová tyč stín 132 cm dlouhý. Určete výšku budovy.
Školní budova vrhá na rovinu dvora stín 16 m dlouhý a v téže době vrhá svislá metrová tyč stín 132 cm dlouhý. Určete výšku budovy.
- Přesýpací hodiny
 Přesýpací hodiny sestávají ze dvou shodných nádobek ve tvaru rotačních kuželů. Pro jednoduchost předpokládáme, že koužely se dotýkají pouze svými vrcholy. Písek sahá do poloviny výšky spodního kužele. Po překlopení hodí trvá přesně 21 minut, než se písek
Přesýpací hodiny sestávají ze dvou shodných nádobek ve tvaru rotačních kuželů. Pro jednoduchost předpokládáme, že koužely se dotýkají pouze svými vrcholy. Písek sahá do poloviny výšky spodního kužele. Po překlopení hodí trvá přesně 21 minut, než se písek - Výběr 4
 Výběr trojúhelník, který je podobný zadanému trojúhelníku. ∆ RTG, r= 24 dm, t = 28 dm, g= 30 dm. - ∆ SHV= 6 dm, h= 7,5 dm, v= 7 dm - ∆ VSH= v= 7 dm, s= 6 dm, h= 7,5 dm -∆ HVS= h= 7,5 dm, v= 7 dm, s = 6 dm. - ∆ VHS= v= 7 dm, h = 7,5 dm, s= 6 dm. - ∆ HSV= h
Výběr trojúhelník, který je podobný zadanému trojúhelníku. ∆ RTG, r= 24 dm, t = 28 dm, g= 30 dm. - ∆ SHV= 6 dm, h= 7,5 dm, v= 7 dm - ∆ VSH= v= 7 dm, s= 6 dm, h= 7,5 dm -∆ HVS= h= 7,5 dm, v= 7 dm, s = 6 dm. - ∆ VHS= v= 7 dm, h = 7,5 dm, s= 6 dm. - ∆ HSV= h - Vyber 3
 Vyber trojúhelník, který je podobný zadanému trojúhelníku. - ∆ TFC= t= 8 cm, f= 9 cm, c= 7 cm. : ∆ PKU= p= 45 cm, k= 35 cm, u= 40 cm. ∆ UPK= u= 40 cm, p= 45 cm, k= 35 cm. ∆ PUK= p= 45 cm, u= 40 cm, k= 35 cm. ∆ KPU= k= 35 cm, p= 45 cm, u= 40 cm. ∆ KUP= k=
Vyber trojúhelník, který je podobný zadanému trojúhelníku. - ∆ TFC= t= 8 cm, f= 9 cm, c= 7 cm. : ∆ PKU= p= 45 cm, k= 35 cm, u= 40 cm. ∆ UPK= u= 40 cm, p= 45 cm, k= 35 cm. ∆ PUK= p= 45 cm, u= 40 cm, k= 35 cm. ∆ KPU= k= 35 cm, p= 45 cm, u= 40 cm. ∆ KUP= k= - Rozhodni 3
 Rozhodni, jestli jsou trojúhelníky podobné. Vyber mezi Ano/Ne. ∆ YUO: y= 9m, u= 17 m, o= 12 m, ∆ ZXV= z= 207 dm, x= 341 dm, v= 394 dm
Rozhodni, jestli jsou trojúhelníky podobné. Vyber mezi Ano/Ne. ∆ YUO: y= 9m, u= 17 m, o= 12 m, ∆ ZXV= z= 207 dm, x= 341 dm, v= 394 dm - Náhrdelník 77664
 Nicolette vyrábí malý korálkový náramek z 5 červených korálků, 8 fialových korálků a 6 zelených korálků. Velký náhrdelník má stejný poměr korálků jako malý náramek. Pokud velký náhrdelník vyžaduje 15 červených kuliček, kolik fialových kuliček je zapotřebí
Nicolette vyrábí malý korálkový náramek z 5 červených korálků, 8 fialových korálků a 6 zelených korálků. Velký náhrdelník má stejný poměr korálků jako malý náramek. Pokud velký náhrdelník vyžaduje 15 červených kuliček, kolik fialových kuliček je zapotřebí
- Dva rovnoramenné
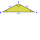 Dva rovnoramenné trojúhelníky mají při vrcholu naproti základně stejný úhel. První z nich má základnu dlouhou 12 cm a rameno 9 cm. Druhý má základnu dlouhou 16 cm. Vypočítej obvod druhého trojúhelníku.
Dva rovnoramenné trojúhelníky mají při vrcholu naproti základně stejný úhel. První z nich má základnu dlouhou 12 cm a rameno 9 cm. Druhý má základnu dlouhou 16 cm. Vypočítej obvod druhého trojúhelníku. - Délka 15
 Délka stínu lípy je 429cm. Délka stínu metrové týče je 78cm. Vypočítej výšku lípy.
Délka stínu lípy je 429cm. Délka stínu metrové týče je 78cm. Vypočítej výšku lípy. - Pětiúhelník
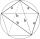 Vývěsní štít má tvar pětiúhelníku ABCDE, ve kterém úsečka BC je kolmá na úsečku AB a EA je kolmá na úsečku AB. Bod P je pata kolmice spuštění z bodu D na úsečku AB. |AP|=|PB|, |BC|=|EA|=6dm, |PD|=8,4dm. Na štítu je vyznačen bod X - průsečík úseček PE a DA
Vývěsní štít má tvar pětiúhelníku ABCDE, ve kterém úsečka BC je kolmá na úsečku AB a EA je kolmá na úsečku AB. Bod P je pata kolmice spuštění z bodu D na úsečku AB. |AP|=|PB|, |BC|=|EA|=6dm, |PD|=8,4dm. Na štítu je vyznačen bod X - průsečík úseček PE a DA - Jsou dány 3
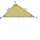 Jsou dány body: A(-3, 1), B (2,-4), C ( 3, 3) a) Určete obvod trojúhelníku ABC. b) Rozhodněte jaký je trojúhelník ABC. c) Určete délku kružnice vepsanej
Jsou dány body: A(-3, 1), B (2,-4), C ( 3, 3) a) Určete obvod trojúhelníku ABC. b) Rozhodněte jaký je trojúhelník ABC. c) Určete délku kružnice vepsanej - Vypočtěte 19
 Vypočtěte výšku stromu, který vrhá stín délky 22 m, víte-li, že ve stejném okamžiku pilíř vysoký 2 m vrhá stín dlouhý 3metry.
Vypočtěte výšku stromu, který vrhá stín délky 22 m, víte-li, že ve stejném okamžiku pilíř vysoký 2 m vrhá stín dlouhý 3metry.
- Podobný
 Pokud trojúhelník ABC ~ (podobný) trojúhelníku XYZ, AC = 24, AB = 15, BC = 17 a XY = 9, jaký je obvod trojúhelníku XYZ? Zaokrouhlete všechny strany na 1 desetinné místo.
Pokud trojúhelník ABC ~ (podobný) trojúhelníku XYZ, AC = 24, AB = 15, BC = 17 a XY = 9, jaký je obvod trojúhelníku XYZ? Zaokrouhlete všechny strany na 1 desetinné místo. - Jak rozdělit
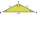 Jak rozdělit rovnoramenný trojúhelník na dvě části o stejných obsazích kolmo na osu souměrnosti (na lichoběžník a trojúhelník)?
Jak rozdělit rovnoramenný trojúhelník na dvě části o stejných obsazích kolmo na osu souměrnosti (na lichoběžník a trojúhelník)? - Ze dvou podobných trojúhelníků
 Ze dvou podobných trojúhelníků má jeden obvod 100 cm, druhý má strany postupně o 8 cm, 14 cm, 18 cm delší než první. Vypočtěte délky jejich stran.
Ze dvou podobných trojúhelníků má jeden obvod 100 cm, druhý má strany postupně o 8 cm, 14 cm, 18 cm delší než první. Vypočtěte délky jejich stran.
