Algebra - slovní úlohy a příklady - strana 221 z 279
Počet nalezených příkladů: 5561
- Klíčivost
 Klíčivost semen je 80% . Z naklíčených rostlin nasledne uhyne 8% . Kolik semen musí zahradnik přichistat, aby vypĕstoval 2000 rostlin?
Klíčivost semen je 80% . Z naklíčených rostlin nasledne uhyne 8% . Kolik semen musí zahradnik přichistat, aby vypĕstoval 2000 rostlin? - Gepard vs antilopa
 Když začal gepard pronásledovat antilopu, byla mezi nimi vzdálenost 120 metrů. Přestože antilopa utíkala rychlostí 72km/h, gepard ji dohonil za 12 sekund. Jakou rychlostí běžel gepard?
Když začal gepard pronásledovat antilopu, byla mezi nimi vzdálenost 120 metrů. Přestože antilopa utíkala rychlostí 72km/h, gepard ji dohonil za 12 sekund. Jakou rychlostí běžel gepard? - Velikost úhlu BVC
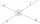 Vypočítej velikost úhlu BVC, pokud pro velikosti úhlů platí: AVB=37°48minut, CVD=52°30minut, AVD=118°
Vypočítej velikost úhlu BVC, pokud pro velikosti úhlů platí: AVB=37°48minut, CVD=52°30minut, AVD=118° - Přímka
 Napište rovnici přímky rovnoběžné s 9x + 3y = 8, která prochází bodem (-1, -4). Napište ve tvaru ax + by = c.
Napište rovnici přímky rovnoběžné s 9x + 3y = 8, která prochází bodem (-1, -4). Napište ve tvaru ax + by = c. - Z kolika
 Z kolika prvků je možné utvořit 120 kombinací druhé třídy?
Z kolika prvků je možné utvořit 120 kombinací druhé třídy? - Variace - druhé třídy - II
 řešte rovnici: V(2, x+8)=72
řešte rovnici: V(2, x+8)=72 - Tloušťka olověné desky
 Intenzita rongenového záření se sníží na polovinu při průchodu vrstvou olova o tloušťce 13,5 mm. Určete tloušťku olověné desky, která zeslabí intenzitu záření na desetinu původní hodnoty. Pokud víme, že intenzita klesá exponenciálně.
Intenzita rongenového záření se sníží na polovinu při průchodu vrstvou olova o tloušťce 13,5 mm. Určete tloušťku olověné desky, která zeslabí intenzitu záření na desetinu původní hodnoty. Pokud víme, že intenzita klesá exponenciálně. - Dva dělníci 9
 Dva dělníci pracují se stejnou výkonností a mohou společně splnit daný úkol za 5 hodin. Jeden dělník provedl na svém stroji zlepšení, změnil pracovní postup a tím zvýšil svůj výkon o 40 %. Za jakou dobu splní nyní oba dělníci daný úkol?
Dva dělníci pracují se stejnou výkonností a mohou společně splnit daný úkol za 5 hodin. Jeden dělník provedl na svém stroji zlepšení, změnil pracovní postup a tím zvýšil svůj výkon o 40 %. Za jakou dobu splní nyní oba dělníci daný úkol? - Bagr vykopal
 Bagr vykopal za 2 hodiny 20 minut 40% výkopu. Jak dlouho mu trvá vykopat celý příkop (výkop)?
Bagr vykopal za 2 hodiny 20 minut 40% výkopu. Jak dlouho mu trvá vykopat celý příkop (výkop)? - Rolník
 Rolník si spočítal, že zásoba krmiva pro jeho 20 krav stačila na 60 dní. Rozhodl se, že prodá 2 krávy a třetinu krmiva. Na jak, dlouho vystačí krmivo pro zbytek rolníkova stáda?
Rolník si spočítal, že zásoba krmiva pro jeho 20 krav stačila na 60 dní. Rozhodl se, že prodá 2 krávy a třetinu krmiva. Na jak, dlouho vystačí krmivo pro zbytek rolníkova stáda? - Heslo
 V rozvodně se každý den mění hlavní heslo, které se skládá z 3 písmen. Způsob generování kódu se však nemění a je založen na následujícím postupu: Následující písmena (A) až (I) odpovídají různým číslicím od 1 do 9. Pokud bychom písmena nahradili číslicem
V rozvodně se každý den mění hlavní heslo, které se skládá z 3 písmen. Způsob generování kódu se však nemění a je založen na následujícím postupu: Následující písmena (A) až (I) odpovídají různým číslicím od 1 do 9. Pokud bychom písmena nahradili číslicem - Bonbony
 Vytvořte 50kg směsi bonbónu o ceně 700Kč. Pokud máme bonbóny o cenách: 820Kč,660Kč a 580Kč. Počítej pomocí křížového pravidla. moc děkuji docela s tím bojujeme
Vytvořte 50kg směsi bonbónu o ceně 700Kč. Pokud máme bonbóny o cenách: 820Kč,660Kč a 580Kč. Počítej pomocí křížového pravidla. moc děkuji docela s tím bojujeme - Vlaky
 Na dvojkolejné trati trati mezi stanicemi K a M jely proti sobě dva vlaky. První vlak projel vzdálenost mezi stanicemi za 3 hodiny, druhý , který měl průměrnou rychlost o 10 km/h větší, ji projel za 2,75 h. Vypočítejte vzdálenost stanic K a M.
Na dvojkolejné trati trati mezi stanicemi K a M jely proti sobě dva vlaky. První vlak projel vzdálenost mezi stanicemi za 3 hodiny, druhý , který měl průměrnou rychlost o 10 km/h větší, ji projel za 2,75 h. Vypočítejte vzdálenost stanic K a M. - Sedmina neznámého
 Sečteme-li sedminu neznámého čísla s jeho šestinou, dostaneme součet 13. které je to číslo? 3.ročník, násobilka
Sečteme-li sedminu neznámého čísla s jeho šestinou, dostaneme součet 13. které je to číslo? 3.ročník, násobilka - Dělitelnost číslem
 V čísle 123 456 789 vynech: a) jednu číslici, aby vzniklo co největší číslo dělitelné 3 b) jednu číslici, aby vzniklo co největší číslo dělitelné 9
V čísle 123 456 789 vynech: a) jednu číslici, aby vzniklo co největší číslo dělitelné 3 b) jednu číslici, aby vzniklo co největší číslo dělitelné 9 - Sum-log
 Součet dvou čísel je 28, součet jejich logaritmů (dekadických) je 1,2. Určitě tato čísla.
Součet dvou čísel je 28, součet jejich logaritmů (dekadických) je 1,2. Určitě tato čísla. - Průměrný věk chlapců
 Průměrný věk dětí ve skupině je 14 let. Ve skupině je 4 krát více chlapců než dívek. Průměrný věk dívek ve skupině je 12 let. Jaký je průměrný věk chlapců?
Průměrný věk dětí ve skupině je 14 let. Ve skupině je 4 krát více chlapců než dívek. Průměrný věk dívek ve skupině je 12 let. Jaký je průměrný věk chlapců? - Pavel 3
 Pavel má vklady na dvou účtech. Jeden na běžném účtu s ročním úrokem 2% a druhý na spořícím účtu s ročním úrokem 4%. Oba vklady mu za rok vynesly 1,000,- Kč. Kdyby přenesl Pavel vklad z jednoho účtu na druhý a naopak, vynesly by mu za rok 1,040,- Kč na úr
Pavel má vklady na dvou účtech. Jeden na běžném účtu s ročním úrokem 2% a druhý na spořícím účtu s ročním úrokem 4%. Oba vklady mu za rok vynesly 1,000,- Kč. Kdyby přenesl Pavel vklad z jednoho účtu na druhý a naopak, vynesly by mu za rok 1,040,- Kč na úr - Zvedání kamene
 Člověk zvedá kámen o hmotnosti 285kg s pomocí páky, která je podepřena ve vzdálenosti 30cm od kamene. Člověk působí na páku ve vzdálenosti 90cm od podpěry. Jak velkou sílu musí člověk vynaložit na zvednutí kamene?
Člověk zvedá kámen o hmotnosti 285kg s pomocí páky, která je podepřena ve vzdálenosti 30cm od kamene. Člověk působí na páku ve vzdálenosti 90cm od podpěry. Jak velkou sílu musí člověk vynaložit na zvednutí kamene? - Míchání roztoků KI
 Vypočítejte objem 50% roztoku KI a objem 20% roztoku KI, které je třeba k přípravě 180g 30% roztoku KI. Jsou známé hustoty roztoků: ρ50%=1,54575 g/cm3, ρ20%=1,16597 g/cm³.
Vypočítejte objem 50% roztoku KI a objem 20% roztoku KI, které je třeba k přípravě 180g 30% roztoku KI. Jsou známé hustoty roztoků: ρ50%=1,54575 g/cm3, ρ20%=1,16597 g/cm³.
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
