Kváder
Kváder ABCDEFGH s výškou 10 cm má podstavné hrany dĺžky 6 cm a 8 cm. Určte odchýlku telesovej uhlopriečky od roviny podstavy (zaokrúhlite na stupne).
Správna odpoveď:
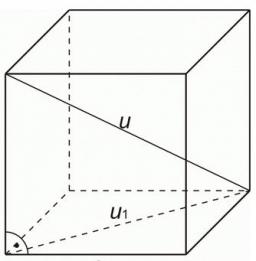
Tipy na súvisiace online kalkulačky
Pytagorova veta je základ výpočtov aj kalkulačky pravouhlého trojuholníka.
Najprirodzenejšou aplikáciou trigonometrie a goniometrických funkcií predstavuje výpočet trojuholníkov. Bežné aj menej bežné výpočty rôznych typov trojuholníkov ponúka naša trigonometrická kalkulačka trojuholníka. Slovo trigonometria pochádza z gréčtiny a doslovne znamená výpočet trojuholníka.
Najprirodzenejšou aplikáciou trigonometrie a goniometrických funkcií predstavuje výpočet trojuholníkov. Bežné aj menej bežné výpočty rôznych typov trojuholníkov ponúka naša trigonometrická kalkulačka trojuholníka. Slovo trigonometria pochádza z gréčtiny a doslovne znamená výpočet trojuholníka.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Kváder
Vypočítajte objem a povrch kvádra ABCDEFGH, ktorého rozmery abc sú v pomere 6:5:9, ak viete že stenová uhlopriečka AC meria 76 cm a má od telesovej uhlopriečky AG má odchýlku 45 stupňov. - Vzdialenosť 47493
Je daný pravidelný štvorboký hranol ABCDEFGH s podstavnou hranou AB dĺžky 8 cm a výškou 6 cm. Bod M je stred hrany AE. Určite vzdialenosť bodu M od roviny BDH. - Vypočítajte 181
Vypočítajte dĺžku telesovej uhlopriečky kvádra s rozmermi 6 cm, 7 cm, 10 cm. Výsledok zaokrúhlite na dve desatinné miesta. - Vypočítajte
Vypočítajte veľkosť odchýlky telesové uhlopriečky a bočné hrany c kvádra s rozmermi: a = 28cm, b = 45cm a c = 73cm. Ďalej vypočítajte veľkosť odchýlky telesové uhlopriečkou od roviny podstavy.
- Objem 40
Objem kvádra so štvorcovou podstavovou je 64 cm³ a odchýlka telesovej uhlopriečky od roviny podstavy je 45 stupňov. Vypočítajte jeho povrch. - Pravidelný
Pravidelný štvorboký ihlan má podstavnou hranu a = 1,56 dm a výšku v = 2,05dm. Vypočítajte: a) odchýlku roviny bočnej steny od roviny podstavy b) odchýlku bočnej hrany od roviny podstavy - Vypočítaj 349
Vypočítaj objem a povrch rotačného kužeľa, ak jeho výška je 10 cm a strana má od roviny podstavy odchýlku 30°.
