Rovnoramenný trojuholník
Rovnoramenný trojuholník ABC má základňu |AB|=16cm a rameno dĺžky 10cm. Aké sú dĺžky ťažníc?
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Vypočet rovnoramenného trojuholníka.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vypočet rovnoramenného trojuholníka.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- planimetria
- Pytagorova veta
- pravouhlý trojuholník
- trojuholník
- kosínusová veta
- goniometria a trigonometria
- sínus
- arkussínus
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Rovnoramenný
 Aké veľké sú uhly rovnoramenného trojuholníka ABC, ak jeho základňa je dlhá a=5 m a rameno b=4 m.
Aké veľké sú uhly rovnoramenného trojuholníka ABC, ak jeho základňa je dlhá a=5 m a rameno b=4 m. - Ťažisko
 V rovnoramennom trojuholníku ABC je pomer dĺžok základne AB a výšky na základňu 10:12. Rameno má dĺžku 26 cm. Ak je T ťažiskom trojuholníka ABC, vypočítajte obsah trojuholníka ABT.
V rovnoramennom trojuholníku ABC je pomer dĺžok základne AB a výšky na základňu 10:12. Rameno má dĺžku 26 cm. Ak je T ťažiskom trojuholníka ABC, vypočítajte obsah trojuholníka ABT. - Narysujte
 Narysujte rovnoramenný trojuholník ABC, ak AB=7cm, veľkosť uhla ABC je 47°, ramená |AC| = |BC|. Odmerajte veľkosť strany BC v mm.
Narysujte rovnoramenný trojuholník ABC, ak AB=7cm, veľkosť uhla ABC je 47°, ramená |AC| = |BC|. Odmerajte veľkosť strany BC v mm. - RR trojuholník
 Vypočítajte výšku na základňu rovnoramenného trojuholníka ABC so základňou AB, AB = c = 10 cm a ramenami a = b = 13 cm
Vypočítajte výšku na základňu rovnoramenného trojuholníka ABC so základňou AB, AB = c = 10 cm a ramenami a = b = 13 cm
- RRT hranol
 Podstava kolmého hranola je rovnoramenný trojuholník, ktorého základňa je 10 cm a rameno 13 cm. Výška hranola je trojnásobok výšky podstavného trojuholníka na jeho základňu. Vypočítajte povrch hranola.
Podstava kolmého hranola je rovnoramenný trojuholník, ktorého základňa je 10 cm a rameno 13 cm. Výška hranola je trojnásobok výšky podstavného trojuholníka na jeho základňu. Vypočítajte povrch hranola. - Rovnoramenný trojuholník
 Vypočítajte obsah a obvod rovnoramenného trojuholníka ABC so základňou AB, a = 6 cm, c = 7 cm.
Vypočítajte obsah a obvod rovnoramenného trojuholníka ABC so základňou AB, a = 6 cm, c = 7 cm. - RR lichobeznik 8
 Zostroj rovnoramenný lichobežník, ktorého základňa má dĺžku 6cm, zviera s uhlopriečkou uhol 30° a ramená majú dĺžku 4cm.
Zostroj rovnoramenný lichobežník, ktorého základňa má dĺžku 6cm, zviera s uhlopriečkou uhol 30° a ramená majú dĺžku 4cm. - RR trojuholník XYZ
 Rovnoramenný trojuholník XYZ má základňu z = 10 cm. Uhol oproti základni je súčtom uhlov pri základni. Vypočítajte obsah trojuholníka XYZ.
Rovnoramenný trojuholník XYZ má základňu z = 10 cm. Uhol oproti základni je súčtom uhlov pri základni. Vypočítajte obsah trojuholníka XYZ. - Rovnoramenný 49
 Rovnoramenný lichobežník ma jednu základňu dvakrát kratšiu ako druhú. Jeho obsah je 42cm² a výška meria 4cm. Vypočítaj jeho obvod, ak vieš že rameno je dlhé 5,3cm.
Rovnoramenný lichobežník ma jednu základňu dvakrát kratšiu ako druhú. Jeho obsah je 42cm² a výška meria 4cm. Vypočítaj jeho obvod, ak vieš že rameno je dlhé 5,3cm.
- Pravouhlý lichobežník
 Pravouhlý lichobežník ABCD, ktorého rameno AD je kolmé na základne AB a CD, má obsah 15cm štvorcových. Základne majú dĺžky AB = 6cm, CD = 4cm. Vypočítaj dĺžku uhlopriečky AC.
Pravouhlý lichobežník ABCD, ktorého rameno AD je kolmé na základne AB a CD, má obsah 15cm štvorcových. Základne majú dĺžky AB = 6cm, CD = 4cm. Vypočítaj dĺžku uhlopriečky AC. - Dva rovnoramenné
 Dva rovnoramenné trojuholníky majú pri vrchole oproti základni uhol rovnakej veľkosti. Jeden z nich má rameno dĺžky 17 cm a základňu dĺžky 10 cm. Druhý má dĺžku základne 8 cm. Urči dĺžku jeho ramena.
Dva rovnoramenné trojuholníky majú pri vrchole oproti základni uhol rovnakej veľkosti. Jeden z nich má rameno dĺžky 17 cm a základňu dĺžky 10 cm. Druhý má dĺžku základne 8 cm. Urči dĺžku jeho ramena. - KOMPARO
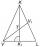 Na obrázku je rovnoramenný trojuholník VLK s ťažiskom T. Základňa VL meria 16 cm, ťažnica KK1 meria 18 cm. Akú dĺžku má ťažnica VV1?
Na obrázku je rovnoramenný trojuholník VLK s ťažiskom T. Základňa VL meria 16 cm, ťažnica KK1 meria 18 cm. Akú dĺžku má ťažnica VV1? - Ťažnice
 Vypočítajte strany pravouhlého trojuholník, ak dĺžky ťažníc na odvesny sú ta=21 cm a tb = 12 cm.
Vypočítajte strany pravouhlého trojuholník, ak dĺžky ťažníc na odvesny sú ta=21 cm a tb = 12 cm. - Trojuholník ABC
 V trojuholníku ABC so stranou BC dĺžky 2 cm je bod K stredom strany AB. Body L a M rozdeľujú stranu AC na tri zhodné úsečky. Trojuholník KLM je rovnoramenný s pravým uhlom pri vrchole K. Určte dĺžky strán AB, AC trojuholníka ABC.
V trojuholníku ABC so stranou BC dĺžky 2 cm je bod K stredom strany AB. Body L a M rozdeľujú stranu AC na tri zhodné úsečky. Trojuholník KLM je rovnoramenný s pravým uhlom pri vrchole K. Určte dĺžky strán AB, AC trojuholníka ABC.
- RR trojuholník
 Je daný rovnoramenný trojuholník ABC, kde AB = AC. Obvod je 64 cm a výška na základňu je 24 cm. Nájdite obsah tohto rovnoramenného trojuholníka
Je daný rovnoramenný trojuholník ABC, kde AB = AC. Obvod je 64 cm a výška na základňu je 24 cm. Nájdite obsah tohto rovnoramenného trojuholníka - Rovnoramenné 67744
 Dva rovnoramenné trojuholníky majú pri vrchole oproti základni rovnaký uhol. Prvý z nich má základňu dlhú 12 cm a rameno 9 cm. Druhý má základňu dlhú 16 cm. Vypočítaj obvod druhého trojuholníka.
Dva rovnoramenné trojuholníky majú pri vrchole oproti základni rovnaký uhol. Prvý z nich má základňu dlhú 12 cm a rameno 9 cm. Druhý má základňu dlhú 16 cm. Vypočítaj obvod druhého trojuholníka. - Rovnoramenný lichobežník
 Vypočítaj obsah rovnoramenného lichobežníka ktorého zakladne sú v pomere 5:3, rameno je dlhé 6cm a výška je 4cm.
Vypočítaj obsah rovnoramenného lichobežníka ktorého zakladne sú v pomere 5:3, rameno je dlhé 6cm a výška je 4cm.
