Príklady na obsah kruhu a kružnice - strana 12 z 19
Počet nájdených príkladov: 372
- Tetiva 24
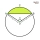 Tetiva s dĺžkou t = r krát druhá odmocnina dvoch rozdeľuje, kruh s polomerom r na dva kruhové odseky. V akom pomere sú obsahy týchto odsekov?
Tetiva s dĺžkou t = r krát druhá odmocnina dvoch rozdeľuje, kruh s polomerom r na dva kruhové odseky. V akom pomere sú obsahy týchto odsekov? - Kružnica - dvoma bodmi
 Napíšte rovnicu kružnice, ktorá prechádza bodmi Q[3,5], R[2,6] a má stred na priamke 2x+3y-4=0.
Napíšte rovnicu kružnice, ktorá prechádza bodmi Q[3,5], R[2,6] a má stred na priamke 2x+3y-4=0. - Súradnice - obdĺžnik
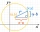 Určite súradnice vrcholu obdĺžnika vpísaného do kružnice x²+y² -2x-4y-20=0, ak viete, že jedna jeho strana leží na priamke p: x+2y=0
Určite súradnice vrcholu obdĺžnika vpísaného do kružnice x²+y² -2x-4y-20=0, ak viete, že jedna jeho strana leží na priamke p: x+2y=0 - Pagáče
 Elena vykrojila z cesta 15 rovnakých pagáčov v tvare kruhu a uložila ich na obdĺžnikový plech tak, aby sa susedné pagáče navzájom dotýkali a pagáče sa po okrajoch dotýkali stien plechu. Každý pagáč zaberal 28,26 cm² dna plechu. Aké rozmery má dno plechu?
Elena vykrojila z cesta 15 rovnakých pagáčov v tvare kruhu a uložila ich na obdĺžnikový plech tak, aby sa susedné pagáče navzájom dotýkali a pagáče sa po okrajoch dotýkali stien plechu. Každý pagáč zaberal 28,26 cm² dna plechu. Aké rozmery má dno plechu? - Oblúkom prepojiť
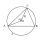 Železnica má prepojiť kruhovým oblúkom miesta A, B a C, ktorých vzdialenosti sú | AB | = 30 km, | AC | = 95 km, | BC | = 70 km. Akú dĺžku bude mať trať z A do C?
Železnica má prepojiť kruhovým oblúkom miesta A, B a C, ktorých vzdialenosti sú | AB | = 30 km, | AC | = 95 km, | BC | = 70 km. Akú dĺžku bude mať trať z A do C? - Kruhový 12
 Kruhový záhon zväčšili tak, že sa jeho polomer zväčšil o 3 m. Spotreba substrátu na zväčšený záhon bola (pri rovnakej výške vrstvy ako pred zväčšením) deväťkrát väčšia ako predtým. Určte pôvodný polomer záhona.
Kruhový záhon zväčšili tak, že sa jeho polomer zväčšil o 3 m. Spotreba substrátu na zväčšený záhon bola (pri rovnakej výške vrstvy ako pred zväčšením) deväťkrát väčšia ako predtým. Určte pôvodný polomer záhona. - odhad priemeru
 Najprv odhadnite, ktorý kruh má väčší priemer: ten, ktorý má rovnaký obsah, ako je rozloha Českej republiky, alebo ten, ktorý má obvod rovný dĺžke hranice Českej republiky? Potom svoj odhad skontrolujte výpočtom. Rozloha SR je 78 864 kilometrov štvorcovýc
Najprv odhadnite, ktorý kruh má väčší priemer: ten, ktorý má rovnaký obsah, ako je rozloha Českej republiky, alebo ten, ktorý má obvod rovný dĺžke hranice Českej republiky? Potom svoj odhad skontrolujte výpočtom. Rozloha SR je 78 864 kilometrov štvorcovýc - Minca 3
 K 200. výročiu narodenia Ľudovíta Štúra vydala Národná banka Slovenska v roku 2015 pamätnú dvojeurovú mincu, ktorej priemer je 25,75mm. Stredná časť z niklovej mosadze má priemer približne 18 milimetrov, zvyšok mince je z mediniklu. Okolo mm² sa líšia plo
K 200. výročiu narodenia Ľudovíta Štúra vydala Národná banka Slovenska v roku 2015 pamätnú dvojeurovú mincu, ktorej priemer je 25,75mm. Stredná časť z niklovej mosadze má priemer približne 18 milimetrov, zvyšok mince je z mediniklu. Okolo mm² sa líšia plo - Šarkan 5
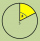 Šarkan má tvar kruhového výseku so stredovým uhlom 40° a polomerom 35 cm. Koľko papiera potrebujeme na zhotovenie, ak na zahnuté treba pridať 10%?
Šarkan má tvar kruhového výseku so stredovým uhlom 40° a polomerom 35 cm. Koľko papiera potrebujeme na zhotovenie, ak na zahnuté treba pridať 10%? - Hippokratové mesiačiky
 Vypočítajte súčet obsahov tzv. Hippokratových mesiačikov, ktoré boli zostrojené nad odvesnami pravouhlého trojuholníka (a=6cm, b=8cm). Návod: vypočítajte najprv obsahy polkruhov nad všetkými stranami trojuholníka ABC. Porovnajte súčet obsahov nechtíkov s
Vypočítajte súčet obsahov tzv. Hippokratových mesiačikov, ktoré boli zostrojené nad odvesnami pravouhlého trojuholníka (a=6cm, b=8cm). Návod: vypočítajte najprv obsahy polkruhov nad všetkými stranami trojuholníka ABC. Porovnajte súčet obsahov nechtíkov s - Tri oblúky
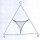 V rovnostrannom trojuholníku o strane 2cm sú zakreslené oblúky troch kružníc so stredmi vo vrcholoch trojuholníka a polomery 1cm. Vypočítaj obsah vyšrafovanej časti - útvaru ktory tvori rozdiel medzi plochou trojuholníka a kruhovými výšok.
V rovnostrannom trojuholníku o strane 2cm sú zakreslené oblúky troch kružníc so stredmi vo vrcholoch trojuholníka a polomery 1cm. Vypočítaj obsah vyšrafovanej časti - útvaru ktory tvori rozdiel medzi plochou trojuholníka a kruhovými výšok. - Medzikružie 6
 Na obrázku sú 2 sústredné kružnice. Tetiva väčšej kružnice s dĺžkou 10 cm je dotyčnicou menšej kružnice. Aký obsah má medzikružie?
Na obrázku sú 2 sústredné kružnice. Tetiva väčšej kružnice s dĺžkou 10 cm je dotyčnicou menšej kružnice. Aký obsah má medzikružie? - Štvorcová záhrada
 Vo štvorcovej záhrade s dĺžkou strany 12 m sú dva kruhové kvetinové záhony s priemerom 4 m a zvyšok záhrady tvorí tráva. Určite plochu, ktorá je zarastená trávou. Koľko percent záhrady zaberajú kvetinové záhony.
Vo štvorcovej záhrade s dĺžkou strany 12 m sú dva kruhové kvetinové záhony s priemerom 4 m a zvyšok záhrady tvorí tráva. Určite plochu, ktorá je zarastená trávou. Koľko percent záhrady zaberajú kvetinové záhony. - Pozemok - pletivo
 Na vašom dvore si chcete vybudovať záhradu, ktorú si chcete oplotiť. Hranica pozemku, na ktorej je postaveny plot, má dĺžku 16m. Na hranici pozemku je postavený plot dlhý 16 metrov. Viacej pletiva na plot nemáme. Akú plochu v metroch štvorcových bude mať
Na vašom dvore si chcete vybudovať záhradu, ktorú si chcete oplotiť. Hranica pozemku, na ktorej je postaveny plot, má dĺžku 16m. Na hranici pozemku je postavený plot dlhý 16 metrov. Viacej pletiva na plot nemáme. Akú plochu v metroch štvorcových bude mať - Vyobrazený obrazec
 Aká veľká je hnedo vyfarbená plocha vo vnútri štvorca o strane 6 cm, ak každá zo štyroch hnedých kruhových úsečí je z kruhu s polomerom dĺžky stany štvorca? Dĺžka kruhových úsečí je rovná dĺžke strany štvorca. Situácia je vyobrazená na obrázku vpravo.
Aká veľká je hnedo vyfarbená plocha vo vnútri štvorca o strane 6 cm, ak každá zo štyroch hnedých kruhových úsečí je z kruhu s polomerom dĺžky stany štvorca? Dĺžka kruhových úsečí je rovná dĺžke strany štvorca. Situácia je vyobrazená na obrázku vpravo. - RT pre hĺbavých
 Trojuholník má preponu 55 a výšku na preponou 33. Aká je plocha trojuholníka?
Trojuholník má preponu 55 a výšku na preponou 33. Aká je plocha trojuholníka? - Záhony
 Pred športovou halou sú dva rovnako veľké obdĺžnikové záhony trávniku, každý s rozmermi 40m a 12m. Údržba 10m² trávnika stojí ročne 45Kč (českých korún). Na každom záhone je kruhový kvetinový záhon o priemere 8m. S koľkými korunami treba ročne počítať na
Pred športovou halou sú dva rovnako veľké obdĺžnikové záhony trávniku, každý s rozmermi 40m a 12m. Údržba 10m² trávnika stojí ročne 45Kč (českých korún). Na každom záhone je kruhový kvetinový záhon o priemere 8m. S koľkými korunami treba ročne počítať na - Stred kružnice
 Je daná ľubovolná kružnica k, ktorá nemá vyznačený stred. Pomocou vhodnej konštrukcie nájdi stred kružnice k. Vyskúšaj na 2 rôznych kružniciach.
Je daná ľubovolná kružnica k, ktorá nemá vyznačený stred. Pomocou vhodnej konštrukcie nájdi stred kružnice k. Vyskúšaj na 2 rôznych kružniciach. - Rozmery trojuholníka
 V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C je dané : a=17cm, Vc=8 cm. Vypočítajte dĺžku strán b, c, jeho obsah S, obvod o, dĺžku polomerov kružníc trojuholníka opísané R a vpísané r a veľkosť uhlov alfa a beta.
V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C je dané : a=17cm, Vc=8 cm. Vypočítajte dĺžku strán b, c, jeho obsah S, obvod o, dĺžku polomerov kružníc trojuholníka opísané R a vpísané r a veľkosť uhlov alfa a beta. - Argandov diagram
 Nech komplexné číslo z=-√2-√2i, kde i² = -1. Nájdite |z|, arg(z), z* (kde * označuje komplexný konjugát) a (1/z). V prípade potreby napíšte svoje odpovede v tvare a + i b, kde a aj b sú reálne čísla. Označte polohy čísel z, z* a (1/z) na Argandovom diagra
Nech komplexné číslo z=-√2-√2i, kde i² = -1. Nájdite |z|, arg(z), z* (kde * označuje komplexný konjugát) a (1/z). V prípade potreby napíšte svoje odpovede v tvare a + i b, kde a aj b sú reálne čísla. Označte polohy čísel z, z* a (1/z) na Argandovom diagra
Máš úlohu, ktorú si tu nenašiel vyriešenú? Pošli nám túto úlohu a my Ti ju skúsime vypočítať. Riešime príklady a úlohy z matematiky. Nielen domáce.
