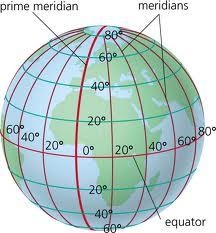
Rovnoběžka
Vypočítejte délku rovnoběžky 48 stupňů a 10 minut.
Správná odpověď:
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Do rovnostranného 2
 Do rovnostranného kužele s průměrem podstavy 12 cm je vepsána koule. Vypočtěte objem obou těles. Kolik procent objemu kužele vyplňuje vepsaná koule?
Do rovnostranného kužele s průměrem podstavy 12 cm je vepsána koule. Vypočtěte objem obou těles. Kolik procent objemu kužele vyplňuje vepsaná koule? - Felix
 Vypočítejte jakou část Země Felix Baumgartner viděl při seskoku z výšky 24 km. Poloměr Země je R = 6378 km.
Vypočítejte jakou část Země Felix Baumgartner viděl při seskoku z výšky 24 km. Poloměr Země je R = 6378 km. - Do odměrného
 Do odměrného válce o vnitřním průměru 10 cm jsou uloženy 4 kovové koule o průměru 5 cm. Jaké nejmenší množství vody je třeba do válce nalít, aby všecky 4 koule byly pod hladinou?
Do odměrného válce o vnitřním průměru 10 cm jsou uloženy 4 kovové koule o průměru 5 cm. Jaké nejmenší množství vody je třeba do válce nalít, aby všecky 4 koule byly pod hladinou? - Na louce
 Na louce přistála kosmická loď ve tvaru koule o průměru 6 m. Aby nepoutala pozornost, zakryli ji marťanci střechou ve tvaru pravidelného kužele. Jak vysoká bude tato střecha, aby spotřeba krytiny byla minimální?
Na louce přistála kosmická loď ve tvaru koule o průměru 6 m. Aby nepoutala pozornost, zakryli ji marťanci střechou ve tvaru pravidelného kužele. Jak vysoká bude tato střecha, aby spotřeba krytiny byla minimální?
- Kulový
 Kulový výsek, jehož osový řez má ve středu koule úhel o velikosti j = 120°, je částí koule o poloměru r = 10 cm. Vypočtěte povrch výseku.
Kulový výsek, jehož osový řez má ve středu koule úhel o velikosti j = 120°, je částí koule o poloměru r = 10 cm. Vypočtěte povrch výseku. - Koule ve kuželi
 Do kužele je vepsána koule (průnik jejich hranic se skládá z kružnice a jednoho bodu). Poměr povrchu koule a obsahu podstavy je 4:3. Rovina, která prochází osou kužele, řeže kužel v rovnoramenném trojúhelníku. Určete velikost úhlu oproti základně tohoto t
Do kužele je vepsána koule (průnik jejich hranic se skládá z kružnice a jednoho bodu). Poměr povrchu koule a obsahu podstavy je 4:3. Rovina, která prochází osou kužele, řeže kužel v rovnoramenném trojúhelníku. Určete velikost úhlu oproti základně tohoto t - Kulová úseč 3
 Kulová úseč má poloměr podstavy 8cm a výšku 5 cm. Vypočítejte poloměr koule, jejíž částí je tato kulová úseč.
Kulová úseč má poloměr podstavy 8cm a výšku 5 cm. Vypočítejte poloměr koule, jejíž částí je tato kulová úseč. - Astronaut
 Jaké procento zemského povrchu vidí astronaut z výšky h = 350 km. Vezměte Zemi jako kouli s poloměrem R = 6370 km
Jaké procento zemského povrchu vidí astronaut z výšky h = 350 km. Vezměte Zemi jako kouli s poloměrem R = 6370 km - Tropické zóny
 Jaké procento zemského povrchu leží v tropické, mírné a polární zóně? Jednotlivé zóny jsou ohraničeny tropy 23° 27 'a polárními kruhy 66° 33'
Jaké procento zemského povrchu leží v tropické, mírné a polární zóně? Jednotlivé zóny jsou ohraničeny tropy 23° 27 'a polárními kruhy 66° 33'
- Kosmicka loď
 Kosmickou loď zpozorovalo radarové zařízení pod výškovým úhlem alpha = 34 stupňů 37 minut a od pozorovacího místa na Zemi měla vzdálenost u = 615km. Vypočítejte vzdálenost d kosmické lodi od Země v okamžiku pozorování. Zem považujeme za kouli s poloměrem
Kosmickou loď zpozorovalo radarové zařízení pod výškovým úhlem alpha = 34 stupňů 37 minut a od pozorovacího místa na Zemi měla vzdálenost u = 615km. Vypočítejte vzdálenost d kosmické lodi od Země v okamžiku pozorování. Zem považujeme za kouli s poloměrem - Vepsána kružnice krychle
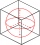 Spodní podstavě krychle o hraně (a=1) je vepsána kružnice. Jaký poloměr má kulová plocha, která obsahuje tuto kružnici a jeden z rohů horní podstavy krychle?
Spodní podstavě krychle o hraně (a=1) je vepsána kružnice. Jaký poloměr má kulová plocha, která obsahuje tuto kružnici a jeden z rohů horní podstavy krychle? - Polokoule 2
 Nádoba tvaru polokoule je zcela naplněna vodou. Jaký poloměr má nádoba, když z ní při naklonění o 30 stupňů vyteče 10 l vody?
Nádoba tvaru polokoule je zcela naplněna vodou. Jaký poloměr má nádoba, když z ní při naklonění o 30 stupňů vyteče 10 l vody? - Na válec
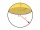 Na válec o průměru 4,6 cm nasaďte část koule tak, aby povrch této části byl 20 cm². Určete r koule ze které byl vrchlík seříznut.
Na válec o průměru 4,6 cm nasaďte část koule tak, aby povrch této části byl 20 cm². Určete r koule ze které byl vrchlík seříznut. - Koule 18
 Koule o poloměru 1 m je postavena do rohu místnosti. Jaká je největší velikost koule, která se vejde do kouta za ní?
Koule o poloměru 1 m je postavena do rohu místnosti. Jaká je největší velikost koule, která se vejde do kouta za ní?
- Letec
 Jak vysoko musí být letec, má-li vidět 0,001 zemského povrchu?
Jak vysoko musí být letec, má-li vidět 0,001 zemského povrchu? - Cukrářka 2
 Cukrářka potřebuje z cukrářské hmoty ve tvaru koule o poloměru 25cm vyřezat ozdobu ve tvaru kužele. Určete poloměr podstavy ozdoby a (a výšku h) tak, aby se na výrobu ozdoby použilo co nejvíce hmoty.
Cukrářka potřebuje z cukrářské hmoty ve tvaru koule o poloměru 25cm vyřezat ozdobu ve tvaru kužele. Určete poloměr podstavy ozdoby a (a výšku h) tak, aby se na výrobu ozdoby použilo co nejvíce hmoty. - Koule
 Najděte rovnici koule pokud na povrchu koule leží tři body (a, 0,0), (0, a, 0), (0,0, a) a střed leží na rovině x + y + z = a.
Najděte rovnici koule pokud na povrchu koule leží tři body (a, 0,0), (0, a, 0), (0,0, a) a střed leží na rovině x + y + z = a.
