Planimetrie - slovní úlohy a příklady - strana 158 z 177
Počet nalezených příkladů: 3524
- Kruhová 4
 Kruhová úseč má obsah 6,04 cm², středový úhel omega je 15 stupňů, jaký je poloměr?
Kruhová úseč má obsah 6,04 cm², středový úhel omega je 15 stupňů, jaký je poloměr? - Délka oblouku
 Oblouk má poloměr 3,3 m. Rozpon je 3,25 m a je 20 cm nad zemí. Jaká délka oblouku je potřeba, aby oblouk dosáhl až na zem?
Oblouk má poloměr 3,3 m. Rozpon je 3,25 m a je 20 cm nad zemí. Jaká délka oblouku je potřeba, aby oblouk dosáhl až na zem? - Trojúhelník - pravoúhlý
 V trojúhelníku ABC, pravoúhlý úhel je na vrcholu B. Strany/AB/=7cm, /BC/=5cm, /AC/=8,6cm. Najděte na dvě desetinná místa. A. sinus úhlu C (gama) B. Kosinus úhlu C C. Tangens úhlu C .
V trojúhelníku ABC, pravoúhlý úhel je na vrcholu B. Strany/AB/=7cm, /BC/=5cm, /AC/=8,6cm. Najděte na dvě desetinná místa. A. sinus úhlu C (gama) B. Kosinus úhlu C C. Tangens úhlu C . - Jak velký 4
 Jak velký uhel je když jedna strana ma 20m a druhá ma 1,5m u pravouhleho trojúhelníku?
Jak velký uhel je když jedna strana ma 20m a druhá ma 1,5m u pravouhleho trojúhelníku? - Komín
 Jak vysoký je komín, vidíme-li ho ze vzdálenosti 60 m pod úhlem 42°?
Jak vysoký je komín, vidíme-li ho ze vzdálenosti 60 m pod úhlem 42°? - Poloměr kružnice
 V rovnoramenném trojúhelníku KLM je základna KL dlouhá 24 cm a rameno měří 15 cm. Jaký je poloměr kružnice popisované tomuto trojúhelníku?
V rovnoramenném trojúhelníku KLM je základna KL dlouhá 24 cm a rameno měří 15 cm. Jaký je poloměr kružnice popisované tomuto trojúhelníku? - Dvojpól RC
 Pro dvojpól vypočtěte komplexní zdánlivý výkon S a okamžitou hodnotu proudu i(t), je-li dáno: R=10 Ω, C=100uF, f=50 Hz, u(t)= druhá odmocnina ze 2, sin( ωt - 30°). Díky za případnou pomoc nebo radu.
Pro dvojpól vypočtěte komplexní zdánlivý výkon S a okamžitou hodnotu proudu i(t), je-li dáno: R=10 Ω, C=100uF, f=50 Hz, u(t)= druhá odmocnina ze 2, sin( ωt - 30°). Díky za případnou pomoc nebo radu. - ABC - 2SU
 Řešte trojúhelník ABC je-li dáno: A = 50°, b = 13, c = 6
Řešte trojúhelník ABC je-li dáno: A = 50°, b = 13, c = 6 - Trojúhelník
 Vypočítejte obsah pravoúhlého trojúhelníku ΔABC, pokud jedna odvěsna je dlouhá 16 a protilehlý úhel je 56°.
Vypočítejte obsah pravoúhlého trojúhelníku ΔABC, pokud jedna odvěsna je dlouhá 16 a protilehlý úhel je 56°. - Stožár
 Stožár elektrického vedení vrhá 17 m dlouhý stín na stráň která stoupá od paty stožáru ve směru stínu pod úhlem o velikosti 5,3°.Určete výšku stožáru jestliže výška Slunce nad obzorem je 40°48'.
Stožár elektrického vedení vrhá 17 m dlouhý stín na stráň která stoupá od paty stožáru ve směru stínu pod úhlem o velikosti 5,3°.Určete výšku stožáru jestliže výška Slunce nad obzorem je 40°48'. - Těžnice RR trojúhelníku
 Rovnoramenný trojúhelník ABC má základnu | AB | = 16cm a rameno délky 10cm. Jaké jsou délky těžnic?
Rovnoramenný trojúhelník ABC má základnu | AB | = 16cm a rameno délky 10cm. Jaké jsou délky těžnic? - Obsah a úhly
 Vypočítej velikosti všech stran a vnitřních úhlů trojúhelníku ABC, jestliže je dáno: S = 501,9; α = 15°28' a β = 45°.
Vypočítej velikosti všech stran a vnitřních úhlů trojúhelníku ABC, jestliže je dáno: S = 501,9; α = 15°28' a β = 45°. - V lichoběžníku 4
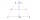 V lichoběžníku ABCD platí : |AD|=|CD|=|BC| a |AB|=|AC|. Urči velikost úhlu delta.
V lichoběžníku ABCD platí : |AD|=|CD|=|BC| a |AB|=|AC|. Urči velikost úhlu delta. - Podobný trojúhelník
 Strany trojúhelníku ABC mají délky 4 cm,5 cm a 7 cm. Sestroj trojúhelník A´B´C´ podobný trojúhelníku ABC, který má obvod 12 cm.
Strany trojúhelníku ABC mají délky 4 cm,5 cm a 7 cm. Sestroj trojúhelník A´B´C´ podobný trojúhelníku ABC, který má obvod 12 cm. - Úhel x
 Úhel x je oproti straně AB, která je dlouhá 10 a strana AC je dlouhá 15 a je přeponou v trojúhelníku ABC. Vypočtěte úhel x.
Úhel x je oproti straně AB, která je dlouhá 10 a strana AC je dlouhá 15 a je přeponou v trojúhelníku ABC. Vypočtěte úhel x. - Kosínus
 Bod [8, 6] leží na koncové straně úhlu θ. cos θ = ...
Bod [8, 6] leží na koncové straně úhlu θ. cos θ = ... - Kosinusova
 Kosinusova a sinusova věta : Vypočítejte všechny chybějící hodnoty z trojúhelníku ABC. a = 20 cm; b = 15 cm; γ = 90°; c =? cm; α =? °; β =? °
Kosinusova a sinusova věta : Vypočítejte všechny chybějící hodnoty z trojúhelníku ABC. a = 20 cm; b = 15 cm; γ = 90°; c =? cm; α =? °; β =? ° - Máme rovnoběžník
 Máme rovnoběžník ABCD, kde AB je 6,2 cm BC je 5,4 cm AC je 4,8 cm vypočítejte výšku na stranu AB a úhel DAB
Máme rovnoběžník ABCD, kde AB je 6,2 cm BC je 5,4 cm AC je 4,8 cm vypočítejte výšku na stranu AB a úhel DAB - Pravoúhlý trojúhelník
 Vypočítejte chybějící stranu b a vnitřní úhly, obvod a obsah pravoúhlého trojúhelníku pokud a=10 cm a přepona c = 16 cm.
Vypočítejte chybějící stranu b a vnitřní úhly, obvod a obsah pravoúhlého trojúhelníku pokud a=10 cm a přepona c = 16 cm. - Trojúhelník ABC 2
 Trojúhelník ABC má délky stran a = 14 cm, b = 20 cm, c = 7,5 cm. Zjisti velikosti úhlů a obsah tohoto trojúhelníku.
Trojúhelník ABC má délky stran a = 14 cm, b = 20 cm, c = 7,5 cm. Zjisti velikosti úhlů a obsah tohoto trojúhelníku.
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
