Stereometrie - slovní úlohy a příklady - strana 112 z 119
Počet nalezených příkladů: 2367
- Průsečík přímky a roviny
Je dán pravidelný čtyřboký jehlan ABCDV, uvnitř jeho hrany AV je bod M, na prosloužené úsečce DC za bod C je bod N. Sestrojte průsečnici roviny MNV s rovinou BCV a průsečík přímky MN a roviny BCV. - Seříznutý kužel
Horní a dolní poloměr seříznutého pravého kruhového kužele je 8 cm a 32 cm. Je-li výška seříznutého okraje 10 cm, jak daleko od spodní základny musí být vytvořena rovina řezu, aby se vytvořily dva podobné seříznuté kužele? - 4-boký jehlan v2
Vypočítejte objem a povrch pravidelného čtyřbokého jehlanu, jeli obsah podstavy 20 cm². Odchylka boční hrany od roviny podstavy je 60 stupňů. - Vodní kanál
Průřez vodního kanálu je lichoběžník. Šířka dna je 19,7 m, šířka vodní hladiny je 28,5 m, boční stěny mají sklon 67°30' a 61°15'. Vypočtěte, jaké množství vody proteče kanálem za 5 minut, pokud rychlost vodního proudu je 0,3 m/s. - Na dvě části
Pravidelný jehlan se čtvercovou podstavou rozřízneme rovinou rovnoběžnou s podstavou na dvě části (viz obrázek). Objem vzniklého menšího jehlanu tvoří 20% objemu původního jehlanu. Podstava vzniklého menšího jehlanu má obsah 10 cm². Určete v centimetrech - Poloha těžiště
Na konci válcové tyče délky 0,8m je připojena koule s poloměrem 0,1m tak, že její střed leží na podélné ose tyče. Obě tělesa jsou ze stejného stejnorodého materiálu. Koule je dvakrát těžší než tyč. Určete polohu těžiště této soustavy těles. - Rovnostranny kužel
Do nádoby tvaru rovnostranného kužele, jehož podstava má poloměr r = 6 cm nalijeme tolik vody, že se naplní jedna třetina objemu kužele. Do jaké výšky bude sahat voda, pokud kužel obrátíme dnem vzhůru?
- Pětiboký jehlan
Vypočtěte objem pravidelného 5-bokého jehlanu ABCDEV, pokud |AB| = 7,7 cm a roviny ABV, ABC svírají úhel 37 stupňů. - Jehlan
Urči povrch pravidelného čtyřbokého jehlanu, když je dán jeho objem V = 120 a úhel boční stěny s rovinou podstavy je α = 42° 30'. - Rozdělit řezem
Daný je kužel s poloměrem podstavy 10 cm a výšce 12 cm. V jaké výšce nad podstavou ho máme rozdělit řezem rovnoběžným s podstavou, aby objemy obou vzniklých teles byly stejné? Výsledek uveďte v cm. - Valec naležato
Válec o průměru 3m a výšce/délce 15 m je položen naležato. Je do něj napuštěna voda, která sahá do výšky 60 cm pod osu válce. Kolik hektolitrů vody je ve válci? - Kužel
Vypočítej objem a povrch kužele, pokud průměr podstavy je d = 14 cm a strana kužele svírá s rovinou podstavy úhel 34°24'. - Velký kužel
Seříznutý rotační kužel má podstavy s poloměry r1 = 8 cm, r2 = 4 cm a výšku v = 5 cm. Jaký je objem kužele, ze kterého komolý kužel vznikl? - Jehlan
Je dán jehlan, podstava a = 7 cm, výška v = 9 cm; a) urči odchylku roviny ABV od roviny podstavy b) odchylku protějších bočních hran - V pravidelném 5
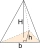V pravidelném trojbokém jehlanu ABCV je odchylka boční stěny a roviny podstavy α = 45°. Určete odchylku boční hrany a roviny podstavy.
- Krabice
Vypočítaj spotřebu papíru na krabici tvaru čtyřbokého hranolu s kosočtvercovou podstavou, podstavná hrana a=6cm, sousedící hrany svírá úhel alfa=60°. výška krabice je 10cm. Kolik m² papíru spotřebujeme na 100 takových krabic? - Pravoúhlý lichoběžník
Uveden je pravoúhlý lichoběžník s mírou ostrého úhlu 50°. Délka jeho podstavců je 4 a 6 jednotek. Objem pevné látky získaný rotací daného lichoběžníku kolem delší základny je: - Kosmicka loď
Kosmickou loď zpozorovalo radarové zařízení pod výškovým úhlem alpha = 34 stupňů 37 minut a od pozorovacího místa na Zemi měla vzdálenost u = 615km. Vypočítejte vzdálenost d kosmické lodi od Země v okamžiku pozorování. Zem považujeme za kouli s poloměrem - Přeřízneme jehlan
Pravidelný čtyřboký jehlan má výšku 40 cm a stranu podstavy 21 cm. Jehlan přeřízneme v poloviční výšce. Jak velký objem budou mít obě části? - Věž
Kolik m² měděného plechu třeba na výměnu střechy věže kuželovitého tvaru, jejíž průměr je 10 m a úhel při vrcholu v osovém řezu je 143°?
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
Viz také více informacií na Wikipedii.
