Laco v Amsterdame
Laco za odmenu išiel (bol vyslaný) na konferenciu do Amsterdamu. Koferencia firmu stála € 1680.
Vypočítajte koľko kníh si mohol namiesto účasti na konferencií kúpiť v cene 56 a 28 eur, ak nechce si doma zapratať knižnicu a môže si kúpiť len 47 kníh?
Vypočítajte koľko kníh si mohol namiesto účasti na konferencií kúpiť v cene 56 a 28 eur, ak nechce si doma zapratať knižnicu a môže si kúpiť len 47 kníh?
Správna odpoveď:

Tipy na súvisiace online kalkulačky
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Téma:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Floor zaokrúhľovanie nadol
 V obore reálnych čísel riešte sústavu rovníc: 2x + ⌊y⌋ = 2022, 3y + ⌊2x⌋ = 2023. (⌊a⌋ označuje (dolnú) celú časť reálneho čísla a, t. j. najväčšie celé číslo, ktoré nie je väčšie ako a. Napr. ⌊1,9⌋ = 1 a ⌊−1,1⌋ = −2.)
V obore reálnych čísel riešte sústavu rovníc: 2x + ⌊y⌋ = 2022, 3y + ⌊2x⌋ = 2023. (⌊a⌋ označuje (dolnú) celú časť reálneho čísla a, t. j. najväčšie celé číslo, ktoré nie je väčšie ako a. Napr. ⌊1,9⌋ = 1 a ⌊−1,1⌋ = −2.) - Dostaneš 42381
 Keď vydelíš neznáme číslo x číslom (-4) a výsledný podiel vydelíš číslom (-3) dostaneš výsledok -2. Koľko je x?
Keď vydelíš neznáme číslo x číslom (-4) a výsledný podiel vydelíš číslom (-3) dostaneš výsledok -2. Koľko je x? - Uchádzači o zamestnanie
 Uchádzači o zamestnanie: tri štvrtiny uchádzačov o prax mali skúsenosti. Počet, ktorý nemal predchádzajúce skúsenosti, bol 36. Koľko ľudí požiadalo o prácu?
Uchádzači o zamestnanie: tri štvrtiny uchádzačov o prax mali skúsenosti. Počet, ktorý nemal predchádzajúce skúsenosti, bol 36. Koľko ľudí požiadalo o prácu? - MO 2019 Z8–I–4
 Pre päticu celých čísel platí, že keď k prvému pripočítame jednotku, druhé umocníme na druhú, od tretieho odčítame trojku, štvrté vynásobíme štyrmi a piate vydelíme piatimi, dostaneme zakaždým ten istý výsledok. Nájdite všetky také pätice čísel, ktorých s
Pre päticu celých čísel platí, že keď k prvému pripočítame jednotku, druhé umocníme na druhú, od tretieho odčítame trojku, štvrté vynásobíme štyrmi a piate vydelíme piatimi, dostaneme zakaždým ten istý výsledok. Nájdite všetky také pätice čísel, ktorých s
- MO Z9-I-6 2019
 Kristína zvolila isté nepárne prirodzené číslo deliteľné tromi. Jakub s Dávidom potom skúmali trojuholníky, ktoré majú obvod v milimetroch rovný Kristínou zvolenému číslu a ktorých strany majú dĺžky v milimetroch vyjadrené navzájom rôznymi celými číslami.
Kristína zvolila isté nepárne prirodzené číslo deliteľné tromi. Jakub s Dávidom potom skúmali trojuholníky, ktoré majú obvod v milimetroch rovný Kristínou zvolenému číslu a ktorých strany majú dĺžky v milimetroch vyjadrené navzájom rôznymi celými číslami. - Na papieri
 Na papieri bolo napísaných niekoľko kladných celých čísel. Miška si pamätala iba to, že každé číslo bolo polovicou súčtu všetkých ostatných čísel. Koľko čísel mohlo byť napísaných na papieri?
Na papieri bolo napísaných niekoľko kladných celých čísel. Miška si pamätala iba to, že každé číslo bolo polovicou súčtu všetkých ostatných čísel. Koľko čísel mohlo byť napísaných na papieri? - Z9–I–3 MO 2019
 Pre ktoré celé čísla x je podiel (x+11)/(x+7) celým číslom. Riešení je údajne viac.
Pre ktoré celé čísla x je podiel (x+11)/(x+7) celým číslom. Riešení je údajne viac. - 3968-x=3179 7845
 Riešte rovnicu: 3968-x=3179
Riešte rovnicu: 3968-x=3179 - Nasledujúcich 7556
 Súčet troch po sebe nasledujúcich celých čísel sa rovná trojnásobku prostredného čísla. Určite tieto čísla.
Súčet troch po sebe nasledujúcich celých čísel sa rovná trojnásobku prostredného čísla. Určite tieto čísla.
- Predchádzajúce 7550
 Súčet štyroch po sebe nasledujúcich celých čísel, z ktorých každé nasledujúce je o 5 väčšie, než predchádzajúce, je 2. Určte tieto čísla.
Súčet štyroch po sebe nasledujúcich celých čísel, z ktorých každé nasledujúce je o 5 väčšie, než predchádzajúce, je 2. Určte tieto čísla. - Myslím 7
 Myslím si číslo, zväčším ho o 6. Zväčšené číslo zmenším o 12. Výsledok vynásobím číslom -2. Súčin predelím číslom -8 a dostanem číslo -4. Aké číslo si myslím?
Myslím si číslo, zväčším ho o 6. Zväčšené číslo zmenším o 12. Výsledok vynásobím číslom -2. Súčin predelím číslom -8 a dostanem číslo -4. Aké číslo si myslím? - Na číselnej osi
 Určte celé číslo, ktorého vzdialenosť na číselnej osi od čísla 1 je dvakrát menšia ako vzdialenosť od čísla 6.
Určte celé číslo, ktorého vzdialenosť na číselnej osi od čísla 1 je dvakrát menšia ako vzdialenosť od čísla 6. - Bonbóny
 Máme určitý počet cukríkov (bonbónov) a prázdnych škatuliek. Keď dáme cukríky do krabičiek po desiatich, ostanú 2 cukríky a 8 prázdnych škatuliek, keď po ôsmich, ostane 6 cukríkov a 3 krabičky. Koľko cukríkov a prázdnych škatuliek ostane, keď dáme cukríky
Máme určitý počet cukríkov (bonbónov) a prázdnych škatuliek. Keď dáme cukríky do krabičiek po desiatich, ostanú 2 cukríky a 8 prázdnych škatuliek, keď po ôsmich, ostane 6 cukríkov a 3 krabičky. Koľko cukríkov a prázdnych škatuliek ostane, keď dáme cukríky - Tajomné číslo
 Kúzelník si myslí číslo: "Tajomné číslo najprv vydelím mínus päť, výsledok vydelím tromi, daný podiel vynásobím desiatimi a výsledné číslo vydelím mínus štyrmi. Vyjde mi číslo 5. " Dokážeš tajomné číslo odhaliť?
Kúzelník si myslí číslo: "Tajomné číslo najprv vydelím mínus päť, výsledok vydelím tromi, daný podiel vynásobím desiatimi a výsledné číslo vydelím mínus štyrmi. Vyjde mi číslo 5. " Dokážeš tajomné číslo odhaliť?
- Nájdite 6174
 Nájdite tri po sebe idúce celé čísla, ktorých súčet je -693.
Nájdite tri po sebe idúce celé čísla, ktorých súčet je -693. - Štyri čísla
 Určite také štyri po sebe bezprostredne idúce celé čísla, aby súčin prvých dvoch bol o 70 menší ako súčin nasledujúcich dvoch.
Určite také štyri po sebe bezprostredne idúce celé čísla, aby súčin prvých dvoch bol o 70 menší ako súčin nasledujúcich dvoch. - Tretiu s druhou
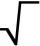 Máme 2 čísla. Keby sme vynásobili tretiu odmocninu prvého čísla s druhou odmocninou druhého čísla, dostali by sme číslo 18.Určte tieto 2 čísla. Ak má úloha v množine reálnych čísel nekonečne veľa riešení, vypočítajte len celočíselné riešenie.
Máme 2 čísla. Keby sme vynásobili tretiu odmocninu prvého čísla s druhou odmocninou druhého čísla, dostali by sme číslo 18.Určte tieto 2 čísla. Ak má úloha v množine reálnych čísel nekonečne veľa riešení, vypočítajte len celočíselné riešenie.
