Klávesy
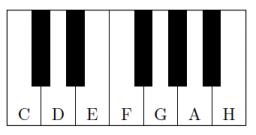
Miško mal na poličke malé klávesy, ktoré vidíte na obrázku. Na bielych klávesoch boli vyznačené ich tóny. Klávesy našla malá Klára. Keď ich brala z poličky, vypadli jej z ruky a všetky biele klávesy sa z nich vysypali. Aby sa brat nehneval, začala je Klára skladať späť. Všimla si pritom, že sa dali vložiť len na niektoré miesta, lebo im prekážali čierne klávesy umiestnené presne do stredu medzi dve biele. Kláre sa podarilo klávesy nejako zložiť, avšak tóny na nich boli pomiešané, pretože ešte nepoznala hudobnú stupnicu. Zistite, koľkými spôsobmi mohla Klára klávesy poskladať...?
Výsledok
Výsledok
Napíšte nám komentár ku príkladu a riešeniu (napríklad ak je stále niečo nejasné...):
Zobrazujem 3 komentáre:
Mo-radca
Nápoveda. Ktoré klávesy mohla Klára zameniť a ktoré nie?
Možné riešenie. Rozsypané, tzn. biele klávesy sú trojakého typu:
1. klávesy C a F, ktoré majú čiernu klávesu sprava,
2. klávesy E a H, ktoré majú čiernu klávesu zľava,
3. klávesy D, G a A, ktoré majú čierne klávesy z oboch strán.
Je zrejmé, že Klára mohla popliesť vždy iba klávesy rovnakého typu.
Klávesy prvého typu mohla poskladať dvojakým spôsobom: C * * F ***, F * * C ***.
Klávesy druhého typu mohla poskladať tiež dvojakým spôsobom: * * E *** H, * * H *** E.
Klávesy tretieho typu mohla poskladať šiestich spôsobmi: * D * * G A *, * D * * A G *, * G * * A D *, * G * * D A *, * A * * D G *, * A * * G D *.
Uvedené tri skupiny možných skladanie sú na sebe úplne nezávislé. Preto je celkový počet možností, ako mohla Klára klávesy poskladať, rovný 2 · 2 · 6 = 24.
Možné riešenie. Rozsypané, tzn. biele klávesy sú trojakého typu:
1. klávesy C a F, ktoré majú čiernu klávesu sprava,
2. klávesy E a H, ktoré majú čiernu klávesu zľava,
3. klávesy D, G a A, ktoré majú čierne klávesy z oboch strán.
Je zrejmé, že Klára mohla popliesť vždy iba klávesy rovnakého typu.
Klávesy prvého typu mohla poskladať dvojakým spôsobom: C * * F ***, F * * C ***.
Klávesy druhého typu mohla poskladať tiež dvojakým spôsobom: * * E *** H, * * H *** E.
Klávesy tretieho typu mohla poskladať šiestich spôsobmi: * D * * G A *, * D * * A G *, * G * * A D *, * G * * D A *, * A * * D G *, * A * * G D *.
Uvedené tri skupiny možných skladanie sú na sebe úplne nezávislé. Preto je celkový počet možností, ako mohla Klára klávesy poskladať, rovný 2 · 2 · 6 = 24.
Na vyriešenie tohto príkladu sú potrebné tieto znalosti z matematiky:
Ďaľšie podobné príklady:
- Úloha roka
Stanovte počet prirodzených čísel od 1 do 106, ktoré končia štvorčíslom 2006. - Myška hryzka
Myška hryzka má 27 kociek, ktoré k sebe poskladala do veľkej kocky. Potom na každej strane vyhryzala prostrednú kocočku a ešte kocočku uprostred. Myška má 4 deti. Potom pozdĺžne kocku rozrieši. Koľko kociek a aký tvar dostanú 4 myšky? - Šach
Koľko spôsobmi je možno na klasickej šachovnici so 64 poliami vybrať 4 polia tak, aby polia nemali rovnakú farbu? - Z7–I–6, výstava mačiek
Na výstave dlhosrstých mačiek sa zišlo celkom desať vystavujúcich. Vystavovalo sa v obdĺžnikovej miestnosti, v ktorej boli dva rady stolov ako na obrázku. Mačky boli označené navzájom rôznymi číslami v rozmedzí 1 až 10 a na každom stole sedela jedna mačka. - Lode
1. Grécka loď odchádza o 6 a vezie kávu. 2. Prostredná loď ma čierny komin. 3. Anglická loď odchádza o deviatej. 4. Francúzska loď je vlavo o lodi vezucej kavu a ma modrý komín . 5. Vpravo od lodi vezúcej kakao je loď idúca do Marseille, 6. Brazilska lod i - Vrecko
V nepriehladnom vrecku sú červené, biele, žlté, modré žetóny, ťaháme 3x po jednom žetóne a opäť ho vrátime, napíš všetky možnosti - Medaila
Koľkými spôsobmi je možné rozdeliť zlatú, striebornú a bronzovú medailu medzi 21 súťažiacich? - Olympiáda
Koľkými spôsobmi sa môžu umiestniť šiesti pretekári na medailových pozíciách na olympiáde? Na farbe kovu záleží. - PIN - kódy
Koľko päťciferných PIN - kódov môžeme vytvoriť s použitím párnych číslic? - Mám 6
Mám 6 druhov zmrzliny a 5 druhov ovocia, do každého pohára ide 3 kopčeky zmrzliny a 2 druhy ovocia. Koľko môže byť pohárov? - Logická
Petra v chorobe navštívili 3 kamaráti, každý v iný deň. Zistite, ktorý deň kto prišiel a čo vybavoval. Prišli v troch dňoch v týždni idúcich za sebou. Prvý prišiel v utorok. Karol v utorok neprišiel. Mirko vybavoval zmenu termínu tréningu, V stredu niesol. - Čísla 13
Koľko prirodzených čísel menších ako 301 možno vytvoriť z číslic 0,1,2,3,6,7? - Šachy
Koľkými možnými spôsobmi sa dá začať šachová partia (prvý ťah)? - Sedem 5
Sedem priateľov sa dohodne, že každý každému pošle pohľadnicu z dovolenky. Koľko pohľadníc bolo odoslaných? - Dôkaz sporom
Chceme dokázať sporom tvrdenie: Ak je prirodzené číslo n deliteľné šiestimi, potom je n deliteľné tromi. Z akého predpokladu budeme vychádzať? - Tréningy
V tabuľke je harmonogram sobotňajších tenisových tréningov mladších žiakov počas zimnej halovej sezóny. Pred začiatkom letnej sezóny sa pripravuje nový harmonogram tréningov. Tomáš Kučera bude môcť trénovať len predpoludním, sestry Kováčové budú musieť tré - Heslo
Kamila si chce zmeniť heslo daliborZ tak, že a) dve spoluhlásky vymení navzájom medzi sebou, b) zmení jednu malú samohlásku na takú istú veľkú samohlásku c) urobí obidve zmeny. Koľko možností má na výber?
