Rebrík
4m rebrík sa dotýka kocky 1mx1m postavené pri stene. Ako vysoko na stene dosiahne?
Správna odpoveď:

Tipy na súvisiace online kalkulačky
Základom výpočtov v analytickej geometrií je dobrá kalkulačka rovnice priamky, ktorá zo súradníc dvoch bodov v rovine vypočíta smernicový, normálový aj parametrický tvar priamky, smernicu, smerový uhol, smerový vektor, dĺžku úsečky, priesečníky so súradnícovými osami atď.
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Priložený 16503
 Rebrík dlhý 8 metrov je priložený k stene pod uhlom 22°. Ako vysoko dosahuje?
Rebrík dlhý 8 metrov je priložený k stene pod uhlom 22°. Ako vysoko dosahuje? - Rebrík 14
 Rebrík dĺžky 3,4 m je opretý o stenu. Jeho dolný koniec je od steny vzdialeny 1,6m. V akej výške sa rebrík dotýka steny?
Rebrík dĺžky 3,4 m je opretý o stenu. Jeho dolný koniec je od steny vzdialeny 1,6m. V akej výške sa rebrík dotýka steny? - Rebrík
 Rebrík dlhý 13 m je opretý o stenu. Jeho päta je vzdialená od steny 1,1 m. V akej výške sa rebrík dotýka steny?
Rebrík dlhý 13 m je opretý o stenu. Jeho päta je vzdialená od steny 1,1 m. V akej výške sa rebrík dotýka steny? - Rebrík
 Rebrík dlhý 7,6 m je opretý o stenu studne a je svojím dolným koncom je vzdialený od tejto steny 1,3 m. Ako vysoko je od dna studne je horný okraj rebríka?
Rebrík dlhý 7,6 m je opretý o stenu studne a je svojím dolným koncom je vzdialený od tejto steny 1,3 m. Ako vysoko je od dna studne je horný okraj rebríka?
- Dvojitý rebrík
 Dvojitý rebrík má ramená dlhé 3 metre. Akú výšku dosiahne horný koniec rebríka, ak sú spodné konce vzdialené 1,8 metra?
Dvojitý rebrík má ramená dlhé 3 metre. Akú výšku dosiahne horný koniec rebríka, ak sú spodné konce vzdialené 1,8 metra? - V akej
 V akej výške sa 15 m rebrík dotýka steny, ak jeho dolný koniec je od steny vzdialený 2,5 m?
V akej výške sa 15 m rebrík dotýka steny, ak jeho dolný koniec je od steny vzdialený 2,5 m? - Rebrík 10m
 Rebrík dlhý 10 metrov je opretý o stenu tak, že jeho spodný okraj je 6 metrov od steny. Ako vysoko siaha rebrík?
Rebrík dlhý 10 metrov je opretý o stenu tak, že jeho spodný okraj je 6 metrov od steny. Ako vysoko siaha rebrík? - Rebrík
 Rebrík dlhý 16 stôp dosahuje až 14 stôp na stene domu. 90-stupňový uhol je na základni domu a steny. Aké sú ďalšie dva uhly a vzdialenosť nohy rebríka od steny?
Rebrík dlhý 16 stôp dosahuje až 14 stôp na stene domu. 90-stupňový uhol je na základni domu a steny. Aké sú ďalšie dva uhly a vzdialenosť nohy rebríka od steny? - O stenu 2
 O stenu je opretý rebrík. Steny sa dotýka vo výške 340 cm a jeho spodný koniec je od steny vzdialený 160 cm. Aký dlhý je rebrík? Výsledok vyjadrite s pres nosťou na centimetre.
O stenu je opretý rebrík. Steny sa dotýka vo výške 340 cm a jeho spodný koniec je od steny vzdialený 160 cm. Aký dlhý je rebrík? Výsledok vyjadrite s pres nosťou na centimetre.
- Je daná 4
 Je daná veľká kocka s hranou dĺžky 3. Ku každej jej stene je prilepená jedna malá kocka s objemom 27-krát menším ako je objem veľkej kocky. Všetky malé kocky sa veľkej dotýkajú celou stenou. Aký povrch má toto teleso?
Je daná veľká kocka s hranou dĺžky 3. Ku každej jej stene je prilepená jedna malá kocka s objemom 27-krát menším ako je objem veľkej kocky. Všetky malé kocky sa veľkej dotýkajú celou stenou. Aký povrch má toto teleso? - Fahrenheit
 Teplota vonku začína pri 0 Fahrenheita. Časom sa teplota mení v rýchlosti -0,6 Fahrenheita za hodinu. Ako dlho trvá, kým teplota dosiahne -4,5 Fahrenheita?
Teplota vonku začína pri 0 Fahrenheita. Časom sa teplota mení v rýchlosti -0,6 Fahrenheita za hodinu. Ako dlho trvá, kým teplota dosiahne -4,5 Fahrenheita? - O stenu
 O stenu je opretý rebrík. Steny sa dotýka vo výške 240cm. A jeho spodný koniec je od steny vzdialený 100 cm. Aký dlhý je rebrík?
O stenu je opretý rebrík. Steny sa dotýka vo výške 240cm. A jeho spodný koniec je od steny vzdialený 100 cm. Aký dlhý je rebrík? - Podstavec z betónu
 Tesári vyrobili drevenú formu na betónový podstavec v tvare kocky o hrane 2 metre. Aký je obsah plochy, v ktorej sa betón dotýka drevenej formy? (Nemá veko ani dno)
Tesári vyrobili drevenú formu na betónový podstavec v tvare kocky o hrane 2 metre. Aký je obsah plochy, v ktorej sa betón dotýka drevenej formy? (Nemá veko ani dno) - Rebrík - M
 Michael má o bok svojho domu opretý 35 stôp dlhý rebrík. Ak je spodná časť rebríka vzdialená 21 stôp od jeho domu, koľko stôp nad zemou sa rebrík dotýka domu?
Michael má o bok svojho domu opretý 35 stôp dlhý rebrík. Ak je spodná časť rebríka vzdialená 21 stôp od jeho domu, koľko stôp nad zemou sa rebrík dotýka domu?
- Papierovej 5890
 Do papierovej krabičky tvaru kocky s objemom 1 liter je zabalený hrnček tvaru valca. Hrnček sa tesne dotýka všetkých stien kocky. Aký má hrnček objem?
Do papierovej krabičky tvaru kocky s objemom 1 liter je zabalený hrnček tvaru valca. Hrnček sa tesne dotýka všetkých stien kocky. Aký má hrnček objem? - Hodnota výrazu
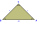 Vzhľadom na to, že p = √(mx/t-t² x) Vytvorte x predmet Ak m = 7, p = -3 a t = 4, nájdite hodnotu x
Vzhľadom na to, že p = √(mx/t-t² x) Vytvorte x predmet Ak m = 7, p = -3 a t = 4, nájdite hodnotu x - Naliali 46191
 Do kocky s dĺžkou hrany 30 cm sme naliali 12 l vody. Ako vysoko siaha hladina vody?
Do kocky s dĺžkou hrany 30 cm sme naliali 12 l vody. Ako vysoko siaha hladina vody?
