V hoteli 2
V hoteli Holiday majú na každom poschodí rovnaký počet izieb. Izby sú číslované prirodzenými číslami postupne od prvého poschodia, žiadne číslo nie je vynechané a každá izba má iné číslo. Do hotela pricestovali traja turisti. Prvý sa ubytoval v izbe číslo 50 na štvrtom poschodí. Druhý v izbe číslo 100 na siedmom poschodí, tretí v izbe číslo 126 na deviatom poschodí. Koľko izieb je na každom poschodí?
Správna odpoveď:

Tipy na súvisiace online kalkulačky
Riešite Diofantovské problémy a hľadáte kalkulačku diofantovských celočíselných rovníc?
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Hotel
 Hotel má p poschodí, na každom poschodí je i izieb, z ktorých je tretina jednolôžkových a ostatné sú dvojlôžkové. Vyjadrite počet lôžok v hoteli.
Hotel má p poschodí, na každom poschodí je i izieb, z ktorých je tretina jednolôžkových a ostatné sú dvojlôžkové. Vyjadrite počet lôžok v hoteli. - Jednoposteľových 6380
 V hoteli majú jednolôžkové a dvojlôžkové izby. Jednoposteľových izieb je o 7 viac ako dvojposteľových. Koľko osôb je ubytovaných na dvojlôžkových izbách, ak je hotel plne obsadený a má kapacitu 100 osôb?
V hoteli majú jednolôžkové a dvojlôžkové izby. Jednoposteľových izieb je o 7 viac ako dvojposteľových. Koľko osôb je ubytovaných na dvojlôžkových izbách, ak je hotel plne obsadený a má kapacitu 100 osôb? - Podkroví 80727
 V hoteli býva polovica ľudí na prvom poschodí, tretina na druhom poschodí a zvyšných 40 hostí v podkroví. Aká sa kapacita hotela, ak je obsadený z 3/4?
V hoteli býva polovica ľudí na prvom poschodí, tretina na druhom poschodí a zvyšných 40 hostí v podkroví. Aká sa kapacita hotela, ak je obsadený z 3/4? - V hoteli 4
 V hoteli označujú čísla izieb 3-cifernym číslom a jedným z písmen A, B. Prva číslica určuje číslo poschodia. Kolko najviac izieb môžu mat v hoteli?
V hoteli označujú čísla izieb 3-cifernym číslom a jedným z písmen A, B. Prva číslica určuje číslo poschodia. Kolko najviac izieb môžu mat v hoteli?
- Napočítal 31051
 Pavol ide ulicou po tej strane, kde sú domy číslované párnymi číslami. Od čísla 2 počíta počet dvojok v číslach domov. Zastaví pri dome, pred ktorým napočítal pätnástu dvojku. Aké je číslo tohto domu?
Pavol ide ulicou po tej strane, kde sú domy číslované párnymi číslami. Od čísla 2 počíta počet dvojok v číslach domov. Zastaví pri dome, pred ktorým napočítal pätnástu dvojku. Aké je číslo tohto domu? - Deľba práce
 Za odvedenu pracu dostali traja pracovníci zaplatené. Prvý dostal 50€, druhý 100 € a tretí 60€. Za dalšiu prácu majú dostať dohomady 735€. Ako si túto sumu rozdelia, ak má byť rozdelená v rovnakom pomere ako prvá práca?
Za odvedenu pracu dostali traja pracovníci zaplatené. Prvý dostal 50€, druhý 100 € a tretí 60€. Za dalšiu prácu majú dostať dohomady 735€. Ako si túto sumu rozdelia, ak má byť rozdelená v rovnakom pomere ako prvá práca? - Brigádnici 3
 Traja brigádnici majú spolu 2850 kč. Prvý dostal o 20% menej ako druhý brigádnik a tretí brigádnik dostal o 50 kč viac ako druhý brigádnik. Kolko kč dostal prvý, druhý a tretí brigádnik?
Traja brigádnici majú spolu 2850 kč. Prvý dostal o 20% menej ako druhý brigádnik a tretí brigádnik dostal o 50 kč viac ako druhý brigádnik. Kolko kč dostal prvý, druhý a tretí brigádnik? - Vzdialenosti 48731
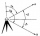 Traja geodeti majú za úlohu zmerať výšku stožiara stojaceho na rovnej pláni. Prvý merač stojaci 100 m od stožiara zmeral výškový uhol (a), druhý vzdialený 200 m od stožiara zmeral výškový uhol (b) a tretí zo vzdialenosti 300 m od stožiara zmeral výškový u
Traja geodeti majú za úlohu zmerať výšku stožiara stojaceho na rovnej pláni. Prvý merač stojaci 100 m od stožiara zmeral výškový uhol (a), druhý vzdialený 200 m od stožiara zmeral výškový uhol (b) a tretí zo vzdialenosti 300 m od stožiara zmeral výškový u - Štvorlôžkových 34461
 Cestovná kancelária má v hoteli rezervované na dva týždne v júli 14 trojlôžkových alebo štvorlôžkových izieb. Koľko trojčlenných a koľko štvorčlenných rodín sa môže najviac na zájazd prihlásiť, ak maximálny počet obsadených sedadiel v autobuse je 50? Zada
Cestovná kancelária má v hoteli rezervované na dva týždne v júli 14 trojlôžkových alebo štvorlôžkových izieb. Koľko trojčlenných a koľko štvorčlenných rodín sa môže najviac na zájazd prihlásiť, ak maximálny počet obsadených sedadiel v autobuse je 50? Zada
- V hoteli 3
 V hoteli je 27 postelí v niekoľkých izbách. Sú tu jednolôžkové, dvojlôžkové a trojlôžkové izby. Koľko môže byť v hoteli jednolôžkových, dvojlôžkových a trojlôžkových izieb? Uveď aspoň tri možnosti.
V hoteli je 27 postelí v niekoľkých izbách. Sú tu jednolôžkové, dvojlôžkové a trojlôžkové izby. Koľko môže byť v hoteli jednolôžkových, dvojlôžkových a trojlôžkových izieb? Uveď aspoň tri možnosti. - Ubytovaných 6906
 Turisti sú ubytovaní v troch hoteloch. V druhom hoteli je ubytovaných o 8 turistov viac ako v prvom av treťom hoteli o 14 viac ako v druhom. Koľko turistu bývali v kazdom hoteli ak ich je spolu 258.
Turisti sú ubytovaní v troch hoteloch. V druhom hoteli je ubytovaných o 8 turistov viac ako v prvom av treťom hoteli o 14 viac ako v druhom. Koľko turistu bývali v kazdom hoteli ak ich je spolu 258. - Guľky
 Traja kamaráti hrali guľky. Na začiatku hry nemali rovnaký počet guliek. Mali ich v pomere 2 : 7 : 5, pričom Mišo a Jano mali spolu 77 guliek. Koľko guliek mal na začiatku ich kamarát Peter? Mohli mať na konci hry všetci rovnaký počet guliek ?
Traja kamaráti hrali guľky. Na začiatku hry nemali rovnaký počet guliek. Mali ich v pomere 2 : 7 : 5, pričom Mišo a Jano mali spolu 77 guliek. Koľko guliek mal na začiatku ich kamarát Peter? Mohli mať na konci hry všetci rovnaký počet guliek ? - Obdĺžniky
 Koľko je obdĺžnikov, ktorých dĺžky strán sú vyjadrené prirodzenými číslami a majú obsah 7644 cm²?
Koľko je obdĺžnikov, ktorých dĺžky strán sú vyjadrené prirodzenými číslami a majú obsah 7644 cm²? - Traja 17
 Traja študenti sa nezávisle od seba pokúšajú vyriešiť úlohu. Prvý študent podobné úlohy vyrieši s pravdepodobnosťou 0,6, druhý študent s pravdepodobnosťou 0,55 a tretí s pravdepodobnosťou 0,04. Úloha je vyriešená, Aká je pravdepodobnosť, že ju vyriešil pr
Traja študenti sa nezávisle od seba pokúšajú vyriešiť úlohu. Prvý študent podobné úlohy vyrieši s pravdepodobnosťou 0,6, druhý študent s pravdepodobnosťou 0,55 a tretí s pravdepodobnosťou 0,04. Úloha je vyriešená, Aká je pravdepodobnosť, že ju vyriešil pr
- Skauti
 Traja skauti išli na trojdňový výlet. Druhý deň prešli o 4km viac ako prvý deň. Tretí deň prešli dvakrát menej ako prvý deň. Spolu prešli 54km. Koľko km prešli každý deň spolu?
Traja skauti išli na trojdňový výlet. Druhý deň prešli o 4km viac ako prvý deň. Tretí deň prešli dvakrát menej ako prvý deň. Spolu prešli 54km. Koľko km prešli každý deň spolu? - Turisti skratka
 Ak traja turisti prejdú trasu za 5 hodín, ako dlho bude tá istá trasa trvať šiestim rovnako rýchlym turistom?
Ak traja turisti prejdú trasu za 5 hodín, ako dlho bude tá istá trasa trvať šiestim rovnako rýchlym turistom? - Školský výlet
 Trieda má 21 žiakov. Akými rôznymi spôsobmi možno žiakov ubytovať v hosteli, ak sú k dispozícií 2× 2-posteľových, 3× 3-posteľových a 2× 4-posteľových izbieb. (Každá izba má svoje unikátne číslo ale postele nie sú číslovné)
Trieda má 21 žiakov. Akými rôznymi spôsobmi možno žiakov ubytovať v hosteli, ak sú k dispozícií 2× 2-posteľových, 3× 3-posteľových a 2× 4-posteľových izbieb. (Každá izba má svoje unikátne číslo ale postele nie sú číslovné)
