Dĺžka - stredná škola - príklady a úlohy - strana 6 z 23
Počet nájdených príkladov: 443
- Bod na priamke
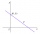 Je daná priamka p a dva vnútorné body jednej z polrovín, určených priamkou p. Nájdi na priamke p bod X tak, aby súčet jeho vzdialeností od bodov A, B bol najmenší.
Je daná priamka p a dva vnútorné body jednej z polrovín, určených priamkou p. Nájdi na priamke p bod X tak, aby súčet jeho vzdialeností od bodov A, B bol najmenší. - Holanďania 36141
 Holanďania ako skupina patria medzi najvyšších ľudí na svete. Priemerný Holanďan je vysoký 184 cm. Ak je vhodné normálne rozdelenie a štandardná odchýlka pre Holanďanov je asi 8 cm, aké je percento Holanďanov, ktorí budú mať viac ako 2 metre?
Holanďania ako skupina patria medzi najvyšších ľudí na svete. Priemerný Holanďan je vysoký 184 cm. Ak je vhodné normálne rozdelenie a štandardná odchýlka pre Holanďanov je asi 8 cm, aké je percento Holanďanov, ktorí budú mať viac ako 2 metre? - Vypočítajte 36061
 V pravidelnom štvorbokom ihlane je dĺžka podstavnej hrany a = 8 cm a dĺžka bočnej hrany h = 17 cm. Vypočítajte povrch ihlana.
V pravidelnom štvorbokom ihlane je dĺžka podstavnej hrany a = 8 cm a dĺžka bočnej hrany h = 17 cm. Vypočítajte povrch ihlana. - Nekoneční desetinný rozvoj
 Určite, ktorá číslica je na 1000. mieste za desatinnou čiarkou v desatinnom rozvoji čísla - zlomku 9/28.
Určite, ktorá číslica je na 1000. mieste za desatinnou čiarkou v desatinnom rozvoji čísla - zlomku 9/28.
- Narysuj 12
 Narysuj rovnoramenný trojuholník ABC so základňou dlhou 7 cm a ramenami dlhými 5,5cm. Zostroj všetky výšky, odmeraj ich a vypočítaj ich súčet
Narysuj rovnoramenný trojuholník ABC so základňou dlhou 7 cm a ramenami dlhými 5,5cm. Zostroj všetky výšky, odmeraj ich a vypočítaj ich súčet - Svetelný rok
 Svetelný rok je jednotka dĺžky, ktorá vyjadruje vzdialenosť, ktorú prejde svetlo za jeden rok. Akú vzdialenosť prejde ak rýchlosť svetla je približne 300 000 km/s?
Svetelný rok je jednotka dĺžky, ktorá vyjadruje vzdialenosť, ktorú prejde svetlo za jeden rok. Akú vzdialenosť prejde ak rýchlosť svetla je približne 300 000 km/s? - Cu vinutie
 Vypočítajte prúd, ktorý prechádza medeným vinutím pri prevádzkovej teplote 70st. Celzia, ak je priemer vinutia 1,128 mm a dĺžka vinutia 40m. Vinutie je pripojené na napätie 8V.
Vypočítajte prúd, ktorý prechádza medeným vinutím pri prevádzkovej teplote 70st. Celzia, ak je priemer vinutia 1,128 mm a dĺžka vinutia 40m. Vinutie je pripojené na napätie 8V. - Osobný a rýchlik
 Po dvojkoľajnej trati jede v jednom smere osobný vlak dĺžky 160m stálou rýchlosťou 54 km/h, v protismere rýchlik dĺžky 240 m. a) Ako veľkou rýchlosťou jede rýchlik, ktorý míňa strojvodca osobného vlaku po dobu 6s? b) Po akú dobu míňa osobný vlak strojvodc
Po dvojkoľajnej trati jede v jednom smere osobný vlak dĺžky 160m stálou rýchlosťou 54 km/h, v protismere rýchlik dĺžky 240 m. a) Ako veľkou rýchlosťou jede rýchlik, ktorý míňa strojvodca osobného vlaku po dobu 6s? b) Po akú dobu míňa osobný vlak strojvodc - Vzdialenosti 34201
 Televízny vysielač vysoký 108 m je ukotvený v 2/3 svojej výšky (od zeme) tromi rovnako dlhými lanami. Koľko metrov lana je treba na ukotvenie, ak je zapustených vo vzdialenosti 54 m od päty stožiara a počítame ešte 10% dĺžky lán na ukotvenie navyše?
Televízny vysielač vysoký 108 m je ukotvený v 2/3 svojej výšky (od zeme) tromi rovnako dlhými lanami. Koľko metrov lana je treba na ukotvenie, ak je zapustených vo vzdialenosti 54 m od päty stožiara a počítame ešte 10% dĺžky lán na ukotvenie navyše?
- Na schodisku
 Na schodisku vysokom 3,6 metrov ak by sa počet schodov zväčšil o 3, keby sa výška jedného schodu zmenšila o 4 cm. Ako sú schody vysoké?
Na schodisku vysokom 3,6 metrov ak by sa počet schodov zväčšil o 3, keby sa výška jedného schodu zmenšila o 4 cm. Ako sú schody vysoké? - Lichobežník PART
 Lichobežník PART s AR || PT (uhol P = x) a (uhol A = 2x). Okrem toho PA = AR = RT = s. Nájdite dĺžku strednej priečky (mediánu) lichobežníka PART, pomocou premennej s.
Lichobežník PART s AR || PT (uhol P = x) a (uhol A = 2x). Okrem toho PA = AR = RT = s. Nájdite dĺžku strednej priečky (mediánu) lichobežníka PART, pomocou premennej s. - Projektil
 Projektil bol vystrelený vo vodorovnom smere z výšky h=25 metrov nad povrchom zeme rýchlosťou v0 = 250 m/s. Určte dostrel a dobu letu projektilu.
Projektil bol vystrelený vo vodorovnom smere z výšky h=25 metrov nad povrchom zeme rýchlosťou v0 = 250 m/s. Určte dostrel a dobu letu projektilu. - Zvislý vrh nahor a nadol
 Teleso vyhodíme z výšky h=5 m nad Zemou zvisle nahor v0=10 m/s. Za aký čas za nim musíme voľne pustiť z tej istej výšky druhé teleso, aby dopadli na Zem súčasne?
Teleso vyhodíme z výšky h=5 m nad Zemou zvisle nahor v0=10 m/s. Za aký čas za nim musíme voľne pustiť z tej istej výšky druhé teleso, aby dopadli na Zem súčasne? - Kolmý priemet
 Určte vzdialenosť bodu B [1, -3] od kolmého priemetu bodu A [3, -2] na priamku 2 x + y + 1 = 0.
Určte vzdialenosť bodu B [1, -3] od kolmého priemetu bodu A [3, -2] na priamku 2 x + y + 1 = 0.
- Súradnice vrcholov
 Sú dané súradnice vrcholov trojuholníka: P (-12,6), Q (4,0), R (-8, -6). Načrtnite obrázok trojuholníka. Nájdite obsah trojuholníka.
Sú dané súradnice vrcholov trojuholníka: P (-12,6), Q (4,0), R (-8, -6). Načrtnite obrázok trojuholníka. Nájdite obsah trojuholníka. - Spomalenie automobilu
 Auto má v určitom mieste svojej dráhy rýchlosť 60 km/h a o 100 m ďalej rýchlosť 40 km/h. Aké je spomalenie auta, ak predpokladáme, že jeho pohyb je rovnomerne spomalený?
Auto má v určitom mieste svojej dráhy rýchlosť 60 km/h a o 100 m ďalej rýchlosť 40 km/h. Aké je spomalenie auta, ak predpokladáme, že jeho pohyb je rovnomerne spomalený? - Šikmý rebrík
 Spodná priečka rebríka je dlhá 36 palcov a najvyššia priečka má dĺžku 24 palcov. Ak má rebrík 18 priečok, o koľko palcov je každá ďalšia priečka kratšia ako priečka pod ním. Koľko stôp (ft) dreva sa použilo na výrobu priečok?
Spodná priečka rebríka je dlhá 36 palcov a najvyššia priečka má dĺžku 24 palcov. Ak má rebrík 18 priečok, o koľko palcov je každá ďalšia priečka kratšia ako priečka pod ním. Koľko stôp (ft) dreva sa použilo na výrobu priečok? - (hydrostatický) 32801
 A) Vypočítaj tlak (hydrostatický) pri dne Mariánskej priekopy. Hustota morskej vody je 1 030 kg/m³. Čo musíš zistiť v atlase či na internete? b) Vypočítaj tlakovú silu pôsobiacu na ponorku s obsahom 2000dm² pri dne tohto priekopy. c) Vypočítaj tlakovú sil
A) Vypočítaj tlak (hydrostatický) pri dne Mariánskej priekopy. Hustota morskej vody je 1 030 kg/m³. Čo musíš zistiť v atlase či na internete? b) Vypočítaj tlakovú silu pôsobiacu na ponorku s obsahom 2000dm² pri dne tohto priekopy. c) Vypočítaj tlakovú sil - Vzdialenými 31871
 Medzi dvoma letiskami vzdialenými 690 km lietajú pravidelné spoje. Z prvého letiska vylieta lietadlo o 6,30 priemernou rýchlosťou o 60 km/h väčšou ako druhé lietadlo, ktoré vylieta z druhého letiska o 7,00. Lietadlá sa vždy míňajú o 9,00. Akou rýchlosťou
Medzi dvoma letiskami vzdialenými 690 km lietajú pravidelné spoje. Z prvého letiska vylieta lietadlo o 6,30 priemernou rýchlosťou o 60 km/h väčšou ako druhé lietadlo, ktoré vylieta z druhého letiska o 7,00. Lietadlá sa vždy míňajú o 9,00. Akou rýchlosťou
Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať.
