PT a kružnice
Řešte pravoúhlý trojúhelník, jsou-li dány poloměry vepsané r=6 a opsané kružnice R=21.
Správná odpověď:
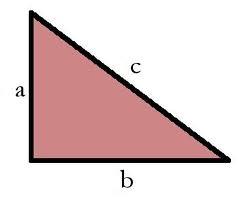
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- RS trojuhélník
 Vypočítejte poloměry kružnice vepsané a opsané rovnostrannému trojúhelníku se stranou a=77 cm.
Vypočítejte poloměry kružnice vepsané a opsané rovnostrannému trojúhelníku se stranou a=77 cm. - V pravoúhlém 2
 V pravoúhlém trojúhelníku ABC jsou známy tyto prvky: a = 10 cm, vc = 9,23 cm. Vypočítejte o, R (poloměr opsané kružnice), r (poloměr vepsané kružnice).
V pravoúhlém trojúhelníku ABC jsou známy tyto prvky: a = 10 cm, vc = 9,23 cm. Vypočítejte o, R (poloměr opsané kružnice), r (poloměr vepsané kružnice). - Vepsaná a opsaná
 Vypočítejte poloměry kružnice vepsané a opsané pravidelnému pětiúhelníku, jehož strana měří 3 cm.
Vypočítejte poloměry kružnice vepsané a opsané pravidelnému pětiúhelníku, jehož strana měří 3 cm. - Rovnoramenný IV
 V rovnoramenném trojúhelníku ABC je |AC| = |BC| = 13. |AB| = 10. Vypočtěte poloměr vepsané (r) a opsané (R) kružnice.
V rovnoramenném trojúhelníku ABC je |AC| = |BC| = 13. |AB| = 10. Vypočtěte poloměr vepsané (r) a opsané (R) kružnice.
- Pravidelný n-uhelnik
 Který pravidelný n-uhelnik má polomer opsane kružnice r=10 cm, a polomer vepsané kružnice p=9,962 cm?
Který pravidelný n-uhelnik má polomer opsane kružnice r=10 cm, a polomer vepsané kružnice p=9,962 cm? - Trojúhelníku 83152
 Daný je rovnoramenný trojúhelník, jehož základna je 8cm a ramena mají délku 15 cm. Vypočítej obsah trojúhelníku a poloměr vepsané a opsané kružnice.
Daný je rovnoramenný trojúhelník, jehož základna je 8cm a ramena mají délku 15 cm. Vypočítej obsah trojúhelníku a poloměr vepsané a opsané kružnice. - Vepsaná a opsaná
 Vypočítej délku kružnice vepsane a kružnice opsane čtverci ABCD so stranou 5cm.
Vypočítej délku kružnice vepsane a kružnice opsane čtverci ABCD so stranou 5cm. - Trojúhelník
 Vypočtěte obsah trojúhelníku ABC je-li dáno: b=c=17 cm, r=19 cm (r je poloměrem kružnice opsané).
Vypočtěte obsah trojúhelníku ABC je-li dáno: b=c=17 cm, r=19 cm (r je poloměrem kružnice opsané). - V pravidelnem 4
 V pravidelnem desetiuhelniku měří pruměr kružnice opsane 10cm. Urči poloměr kružnice vepsane tomuto trojuhelniku.
V pravidelnem desetiuhelniku měří pruměr kružnice opsane 10cm. Urči poloměr kružnice vepsane tomuto trojuhelniku.
- Vypočítejte 20
 Vypočítejte strany pravoúhlého trojúhelníku, je-li zadána, že a+b=17cm, poloměr vepsané kružnice ρ=2cm.
Vypočítejte strany pravoúhlého trojúhelníku, je-li zadána, že a+b=17cm, poloměr vepsané kružnice ρ=2cm. - Decagon
 Vypočtěte obsah a obvod pravidelného desetiúhelníku, je-li dán jeho poloměr kružnice opsané R=1m
Vypočtěte obsah a obvod pravidelného desetiúhelníku, je-li dán jeho poloměr kružnice opsané R=1m - Rovnostrannému 4278
 Rovnostrannému trojúhelníku o délce strany 8 cm je popsána i vepsaná kružnice. O kolik cm je obvod vepsané kružnice menší než obvod opsané kružnice?
Rovnostrannému trojúhelníku o délce strany 8 cm je popsána i vepsaná kružnice. O kolik cm je obvod vepsané kružnice menší než obvod opsané kružnice? - Trojúhelníku 81759
 V trojúhelníku ABC známe a = 4 cm, b = 6 cm, γ = 60°. Vypočítejte obsah, poloměr vepsané a opsané kružnice.
V trojúhelníku ABC známe a = 4 cm, b = 6 cm, γ = 60°. Vypočítejte obsah, poloměr vepsané a opsané kružnice. - Vypočtěte 12
 Vypočtěte povrch a objem pravidelného devítibokého jehlanu, měří-li poloměr kružnice vepsané podstavě ρ= 12 cm a výška jehlanu je 24 cm
Vypočtěte povrch a objem pravidelného devítibokého jehlanu, měří-li poloměr kružnice vepsané podstavě ρ= 12 cm a výška jehlanu je 24 cm
- 30-úhelník
 V pravidelném 30-ti úhelníku je poloměr kružnice vepsané 15cm. Zjištěte velikost hrany „a", poloměr kružnice opsané „R", obvod a obsah.
V pravidelném 30-ti úhelníku je poloměr kružnice vepsané 15cm. Zjištěte velikost hrany „a", poloměr kružnice opsané „R", obvod a obsah. - Nonagon
 Vypočtěte obsah a obvod pravidelného devítiúhelníku, je-li dán jeho poloměr kružnice vepsané r=10cm
Vypočtěte obsah a obvod pravidelného devítiúhelníku, je-li dán jeho poloměr kružnice vepsané r=10cm - Vypočítej 13
 Vypočítej obsah pravidelného šestiúhelníka, je-li poloměr kružnice jemu opsané 6,8 cm.
Vypočítej obsah pravidelného šestiúhelníka, je-li poloměr kružnice jemu opsané 6,8 cm.
