Kužeľ a pomer

Rotačný kužeľ má výšku 23 cm a pomer podstavy k plášťu je 7:9. Vypočítaj podstavu a plášť (t.j. ich obsahy).

Správny výsledok:

S1 =  2544,79 cm2
S2 =  3271,87 cm2

Riešenie:

v=23 S1=πr2 S2=πrs  S1:S2=7/9 πr2πrs=7/9 r/s=7/9 s=r⋅9/7;  s2=v2+r2 r2⋅92/72=232+r2 r2=5291.653−1 r2=810.031 r=810.031=28.46 cm  s=r⋅9/7=36.59 cm  S1=πr2=π28.462=2544.79 cm2
S2=πrs=π⋅28.46⋅36.59=3271.87 cm2

Skúsiť iný príklad


Budeme veľmi radi, ak nájdete chybu v príklade, pravopisné chyby alebo nepresnosť a ju nám prosím pošlete. Ďakujeme!






Zobrazujem 0 komentárov:
avatar




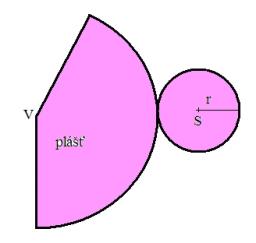
Tipy na súvisiace online kalkulačky
Vyskúšajte našu kalkulačka na prepočet pomeru.
Pytagorova veta je základ výpočtov aj kalkulačky pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.

Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:


 
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1   video2

Ďaľšie podobné príklady a úlohy:

  • Rovnostranný trojuholník
    rs_triangle_1 Rovnostranný trojuholník má stranu dlhú 23 cm. Vypočítaj jeho obsah.
  • Rotačný kužeľ
    kuzel_4 Obsah plášta rotačného kužeľa je 240 cm2 a obsah jeho podstavy 160 cm2. Vypočítaj objem tohto kužeľa.
  • Rotačný 8
    cone_7 Rotačný kúžeľ má výšku 20 cm a polomer 18 cm. Vypočítajte jeho povrch.
  • Stredový uhol
    kuzel2 Plášť kužeľa s polomerom podstavy 20 cm a výškou 50 cm sa rozvinie do kruhového výseku. Aký veľký je stredový uhol tohto výseku ?
  • Pomer 33
    kuzel2 Pomer obsahu podstavy rotačného kužeľa k jeho plášťu je 3 : 5. Vypočítajte povrch a objem kužeľa, ak jeho výška v = 4 cm.
  • Rotačný 9
    kuzel2 Rotačný kužeľ má obvod podstavy 62,8 cm. A výšku 0,7 dm. Vypočítajte jeho povrch a objem.
  • Rotačné telesá
    conecylinder Rotačný kužeľ a rotačný valec majú rovnaký objem 180 cm3 a rovnakú výšku v = 15cm. Ktoré z týchto dvoch telies má väčší povrch?
  • Štvorboký ihlan
    jehlan_4b_obdelnik Vypočítaj povrch štvorbokého ihlanu, ktorý má obdĺžnikovú podstavu s rozmermi a = 8 cm, b = 6 cm a výšku v = 10 cm.
  • Tienidlo
    kuzel_2 Tienidlo v tvare kužeľa má priemer 30 cm a výšku 10 cm. Koľko cm2 materiálu budeme potrebovať, ak počítame 10% na odpad?
  • Plášť 4
    prism_5 Plášť rotačného valca je 4 krát väčší než obsah jeho podstavy. Určte objem pravidelného trojbokého hranola, ktorý je vo valci vpísaný. Polomer podstavy valca je 10 cm.
  • Z plastelíny
    kuzel_1 Miško vymodeloval z plastelíny 15 cm vysoký ihlan s obdĺžnikovou podstavou so stranami podstavy a = 12 cm a b = 8 cm. Janka z tohto ihlanu vymodelovala rotačný kužeľ s priemerom podstavy d = 10 cm. Akú výšku mal Jankin kužeľ?
  • Kruh 23
    described_circle_1 Vypočítaj obsah kruhu, ktorý je opísaný štvorcu so stranou dlhou 7,5 cm.
  • Kužeľ 20
    kuzel3 Vypočítajte objem a plochu kužeľa, ktorého výška je 10 cm a v osovom reze zviera so stenou kužeľa uhol 30 stupňov.
  • Rotačný kúžeľ II
    cone Vypočítajte povrch rotačného kužeľa s polomerom podstavy r=11 cm a výškou v=10 cm.
  • Vypočítaj
    hex_pyramid Vypočítaj prosím výšku pravidelného šesťbokého ihlanu s hranou podstavy 5cm a stenovou výškou w = 20cm. Načrtnite prosím obrázok.
  • Uhlopriečka podstavy
    hranol4sreg_7 Vypočítaj objem a povrch pravidelného štvorbokého hranola vysokého 35 cm, uhlopriečka podstavy je 22 cm.
  • Vypočítaj 78
    kuzel2 Vypočítaj objem kužeľa, ak obsah jeho podstavy je 78,5 cm2 a obsah plášťa je 219,8 cm2.