Pomer 33
Pomer obsahu podstavy rotačného kužeľa k jeho plášťu je 3 : 5. Vypočítajte povrch a objem kužeľa, ak jeho výška v = 4 cm.
Vaša odpoveď:
Vaša odpoveď:
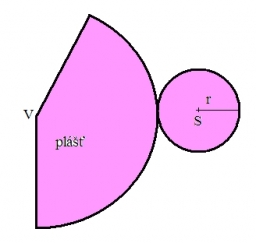
Tipy na súvisiace online kalkulačky
Vyskúšajte našu kalkulačka na prepočet pomeru.
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebrastereometriaplanimetriazákladné operácie a pojmyJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Rotačný kúžeľ
Vypočítajte objem rotačného kužeľa s polomerom podstavy r=10 cm a výškou v=10 cm. - Rotačný kúžeľ - V,v
Povrch rotačného kužeľa a obsah jeho podstavy sú v pomere 18:5. Určte objem kužeľa, ak je jeho telesná výška 12 cm. - Vypočítajte 183
Vypočítajte povrch a objem rotačného kužeľa, ktorého podstava má priemer 6 cm, a jeho výška 4 cm. - Vypočítaj rot kužeľ
Základné parametre rotačného kužeľa sú: Polomer podstavy 5 cm Výška kužeľa 12 cm a strana kužeľa 13 cm. Vypočítaj: a/objem kužeľa b/povrch kužeľa - Zmena objemu
Ako sa zmení objem rotačného kužeľa, ak: a) zdvojnásobíme polomer podstavy b) 3 krát zmenšíme výšku c) 5 krát zmenšíme polomer podstavy - Vypočítaj 349
Vypočítaj objem a povrch rotačného kužeľa, ak jeho výška je 10 cm a strana má od roviny podstavy odchýlku 30°. - Kúžeľ
Vypočítajte objem a povrch rotačného kužeľa s polomerom podstavy r = 2,3 dm a výškou v = 46 mm.
