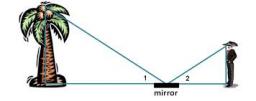
Zrkadielko
Ako ďaleko od svojich nôh musel Pavel umiestniť zrkadlo, aby v ňom uvidel vrchol veže vysokej 12 m? Výška Pavlových očí očí nad horizontálnou rovinou je 160 cm, Pavol je od veže vzdialený 20 m.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Chcete premeniť jednotku dĺžky?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Pozorovateľ 4
 Pozorovateľ vidí pätu veže vysokej 96 metrov pod hĺbkovým uhlom 30 stupňov a 10 minút a vrchol veže pod hĺbkovým uhlom 20 stupňov a 50 minút. Ako vysoko je pozorovateľ nad horizontálnou rovinou, na ktorej stojí veža?
Pozorovateľ vidí pätu veže vysokej 96 metrov pod hĺbkovým uhlom 30 stupňov a 10 minút a vrchol veže pod hĺbkovým uhlom 20 stupňov a 50 minút. Ako vysoko je pozorovateľ nad horizontálnou rovinou, na ktorej stojí veža? - Na vrchole 2
 Na vrchole kopca stojí rozhľadňa 30 m vysoká. Jej pätu a vrchol vidíme z určitého miesta v údolí pod výškovými uhlami a= 28°30", b=30°40". Ako vysoko je vrchol kopca nad horizontálnou rovinou pozorovacieho miesta?
Na vrchole kopca stojí rozhľadňa 30 m vysoká. Jej pätu a vrchol vidíme z určitého miesta v údolí pod výškovými uhlami a= 28°30", b=30°40". Ako vysoko je vrchol kopca nad horizontálnou rovinou pozorovacieho miesta? - Rozhladna 2
 Ako daleko od rozhladne vysokej 48 m stal turista ak jej vrchol videl pod uhlom s velkostou 40°?
Ako daleko od rozhladne vysokej 48 m stal turista ak jej vrchol videl pod uhlom s velkostou 40°? - V hĺbkovom uhle
 Z pozorovacej veže vo výške 105 m nad hladinou mora je zameraná loď v hĺbkovom uhle 1° 49'. Ako ďaleko je loď od päty veže?
Z pozorovacej veže vo výške 105 m nad hladinou mora je zameraná loď v hĺbkovom uhle 1° 49'. Ako ďaleko je loď od päty veže?
- Pozorovateľ 3
 Pozorovateľ vidí vrcholce dvoch stromov v rovnakom uhle a. Od jedného stromu je vzdialený 9 m, od druhého 21 m. Stromy stoja na rovine. Aký vysoký je druhý strom, ak výška prvého je 6 m? Nezabudni, že oči stojaceho človeka sú približne 1,5 m nad zemou.
Pozorovateľ vidí vrcholce dvoch stromov v rovnakom uhle a. Od jedného stromu je vzdialený 9 m, od druhého 21 m. Stromy stoja na rovine. Aký vysoký je druhý strom, ak výška prvého je 6 m? Nezabudni, že oči stojaceho človeka sú približne 1,5 m nad zemou. - Zorný uhol 2
 Pozorovateľ vidí priamu ohradu dlhú 60 m v zornom uhle 30°. Od jedného konca ohrady je vzdialený 102 m. Ako ďaleko je pozorovateľ od druhého konca ohrady?
Pozorovateľ vidí priamu ohradu dlhú 60 m v zornom uhle 30°. Od jedného konca ohrady je vzdialený 102 m. Ako ďaleko je pozorovateľ od druhého konca ohrady? - Jama 4
 Táles je vzdialený 1 m od jamy. Oči má vo výške 150 cm nad zemou a pozerá do jamy s priemerom 120 cm podľa obrázka. Vypočítajte hĺbku jamy.
Táles je vzdialený 1 m od jamy. Oči má vo výške 150 cm nad zemou a pozerá do jamy s priemerom 120 cm podľa obrázka. Vypočítajte hĺbku jamy. - Peter a Pavol
 Ako ďaleko od Petra stojí dvojmetrový Pavol? Peter sa na Pavla pozerá cez pravítko, ktoré drží v natiahnuté v ruke 60 cm od oka a na pravítku zmeral Pavlovu výšku na 15 mm.
Ako ďaleko od Petra stojí dvojmetrový Pavol? Peter sa na Pavla pozerá cez pravítko, ktoré drží v natiahnuté v ruke 60 cm od oka a na pravítku zmeral Pavlovu výšku na 15 mm. - Vzdialený 39741
 Nikolka má z púte balónik na dva metre dlhom povrázku, ktorého koniec drží 60 cm nad zemou. Balónik sa vznáša šikmo od Nikolky a je od nej vodorovne vzdialený 145 cm. V akej výške je balónik od zeme?
Nikolka má z púte balónik na dva metre dlhom povrázku, ktorého koniec drží 60 cm nad zemou. Balónik sa vznáša šikmo od Nikolky a je od nej vodorovne vzdialený 145 cm. V akej výške je balónik od zeme?
- Na vrchole
 Na vrchole hory stojí hrad, ktorý má vežu vysokú 30m. Križovatku ciest v údolí vidíme z vrcholu veže a od jej päty v hlbkovych uhloch 32°50' a 30°10'. Ako vysoko je vrchol hory nad križovatkou?
Na vrchole hory stojí hrad, ktorý má vežu vysokú 30m. Križovatku ciest v údolí vidíme z vrcholu veže a od jej päty v hlbkovych uhloch 32°50' a 30°10'. Ako vysoko je vrchol hory nad križovatkou? - Osobný vlak
 Osobný vlak je vzdialený 60 km od cieľovej stanice a ide rovnomernou rýchlosťou 54 km/h. Ako ďaleko bude od cieľovej stanice o 45 minút?
Osobný vlak je vzdialený 60 km od cieľovej stanice a ide rovnomernou rýchlosťou 54 km/h. Ako ďaleko bude od cieľovej stanice o 45 minút? - Kostolná veža
 Arcidekanský kostol v Ústí nad Labom má sklonenú vežu o 186 cm. Výška veže je 65 m. Vypočítajte veľkosť uhla, o ktorý je veža vychýlená. Výsledok urči v minútach.
Arcidekanský kostol v Ústí nad Labom má sklonenú vežu o 186 cm. Výška veže je 65 m. Vypočítajte veľkosť uhla, o ktorý je veža vychýlená. Výsledok urči v minútach. - Dekanského 5670
 Veža Dekanského chrámu v Ústí nad Labem je odchýlka od pôvodnej zvislej osi o 220 cm. Jej pôvodná výška bola 48 m. V akej výške sa teraz nachádza najvyšší bod tejto veže? Výsledok uveďte s presnosťou na centimetre.
Veža Dekanského chrámu v Ústí nad Labem je odchýlka od pôvodnej zvislej osi o 220 cm. Jej pôvodná výška bola 48 m. V akej výške sa teraz nachádza najvyšší bod tejto veže? Výsledok uveďte s presnosťou na centimetre. - Strom 2
 Strom bol vysoký 35m. Strom sa zlomil vo výške 10 m nad zemou. Vršok ale neodpadol, len sa vyvrátil na zem. Ako ďaleko od päty stromu ležala jeho špička?
Strom bol vysoký 35m. Strom sa zlomil vo výške 10 m nad zemou. Vršok ale neodpadol, len sa vyvrátil na zem. Ako ďaleko od päty stromu ležala jeho špička?
- Pozorujeme 76644
 Ako ďaleko od seba sú rozhľadne, ak z menšej pozorujeme vrchol väčšej rozhľadne pod výškovým uhlom 23 ° a rozdiel v ich výškach je 12m?
Ako ďaleko od seba sú rozhľadne, ak z menšej pozorujeme vrchol väčšej rozhľadne pod výškovým uhlom 23 ° a rozdiel v ich výškach je 12m? - More
 Ako ďaleko vidieť na šírom mori z lodného stožiara, ktorého vrchol je 14 metrov nad hladinou vody? (Polomer Zeme je 6370 km.)
Ako ďaleko vidieť na šírom mori z lodného stožiara, ktorého vrchol je 14 metrov nad hladinou vody? (Polomer Zeme je 6370 km.) - Piasiatká
 V zoo bol výbeh pre domáce zvieratká. Boli v ňom sliepky, prasiatka a krava. Dokopy tam bolo 20 hláv a 60 nôh. Koľko bolo sliepok a koľko prasiatok?
V zoo bol výbeh pre domáce zvieratká. Boli v ňom sliepky, prasiatka a krava. Dokopy tam bolo 20 hláv a 60 nôh. Koľko bolo sliepok a koľko prasiatok?
