Vepsaná kružnice
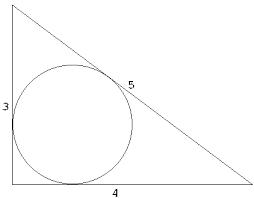
Vypočítejte obvod a obsah vepsané kružnice do trojúhelníku s rozměry 3 4 a 5 cm.
Správná odpověď:
Zobrazuji 1 komentář:
Žák
Q: Blbost. Obvod kružnice nemůže být nikdy víc než obsah kružnice.
A: A to sa v ktorej ucebnici matematiky pise? Pre male polomery kruznice napr. mensie nez jedna, je to ukazkovy pripad, kedy toto tvrdenie neplati.
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Úroveň náročnosti úkolu:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Vzdálenost 145
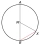 Vzdálenost tětivy od středu je 6 cm. Středový úhel je 60°. Vypočítejte plošný obsah kruhové úseče.
Vzdálenost tětivy od středu je 6 cm. Středový úhel je 60°. Vypočítejte plošný obsah kruhové úseče. - Kruh - úseč
 Kruh o průměru 30 cm je přeťat tětivou t = 16 cm. Vypočtěte obvod a obsah menší úseče.
Kruh o průměru 30 cm je přeťat tětivou t = 16 cm. Vypočtěte obvod a obsah menší úseče. - Úhlopříčkou 3
 Úhlopříčkou řezu DBFH pravidelného čtyřbokého hranolu ABCDEFGH je vepsán kruh o průměru 8 cm. Jaký je objem hranolu.
Úhlopříčkou řezu DBFH pravidelného čtyřbokého hranolu ABCDEFGH je vepsán kruh o průměru 8 cm. Jaký je objem hranolu. - Katka 7
 Katka si objednala dort ve tvaru valce o objemu 15,7l. Skládá se ze dvou pater. Objem horního patra je 4x menší než objem dolního patra. Výška obou pater stejna a je rovná polomeru horního patra dortu. Katka rozkrojila dort kolmo k podložce na 2 stejně čá
Katka si objednala dort ve tvaru valce o objemu 15,7l. Skládá se ze dvou pater. Objem horního patra je 4x menší než objem dolního patra. Výška obou pater stejna a je rovná polomeru horního patra dortu. Katka rozkrojila dort kolmo k podložce na 2 stejně čá
- Kruhová 4
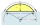 Kruhová úseč má obsah 6,04 cm², středový úhel omega je 15 stupňů, jaký je poloměr?
Kruhová úseč má obsah 6,04 cm², středový úhel omega je 15 stupňů, jaký je poloměr? - Truhlář 5
 Truhlář opracovával rotační válec s poloměrem podstavy 2,5dm a výškou 2dm. Rovnoměrným broušením zmenšil poloměr o 1cm, výška válce byla zachována. Vypocitej, o kolik procent se zmenšil obsah válce.
Truhlář opracovával rotační válec s poloměrem podstavy 2,5dm a výškou 2dm. Rovnoměrným broušením zmenšil poloměr o 1cm, výška válce byla zachována. Vypocitej, o kolik procent se zmenšil obsah válce. - Poloměr 12
 Poloměr kruhového záhonu je 2 m. Okolo něho je plocha vysypaná pískem, jejíž hranici tvoří strany čtverce o délce 5 m a obvod záhonu. Vypočítejte obsah plochy vysypané pískem.
Poloměr kruhového záhonu je 2 m. Okolo něho je plocha vysypaná pískem, jejíž hranici tvoří strany čtverce o délce 5 m a obvod záhonu. Vypočítejte obsah plochy vysypané pískem. - Chceme-li 81397
 Dětský bazén má tvar válce o průměru podstavy 4 m a hloubce 50 cm (náčrt, výpočet, odpověď). a) Vypočítej objem vody v litrech, který může být v bazénu, je-li naplněn po okraj. b) Pokud bazén naplníme jen na 75%, kolik litrů vody bude v bazénu? c) Chceme-
Dětský bazén má tvar válce o průměru podstavy 4 m a hloubce 50 cm (náčrt, výpočet, odpověď). a) Vypočítej objem vody v litrech, který může být v bazénu, je-li naplněn po okraj. b) Pokud bazén naplníme jen na 75%, kolik litrů vody bude v bazénu? c) Chceme- - Minutová 8
 Minutová ručička je třikrát delší než sekundová. V jakém poměru jsou velikosti rychlostí jejich koncových bodů?
Minutová ručička je třikrát delší než sekundová. V jakém poměru jsou velikosti rychlostí jejich koncových bodů?
- Poloměr 10
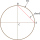 Poloměr kružnice r=8,9 cm, tětiva AB této kružnice má délku 16 cm. Vypočítej vzdálenost tětivy AB od středu kružnice .
Poloměr kružnice r=8,9 cm, tětiva AB této kružnice má délku 16 cm. Vypočítej vzdálenost tětivy AB od středu kružnice . - Do kruhu
 Do kruhu s průměrem 20cm byl vepsán pravoúhlý trojúhelník, jehož přepona je průměrem kruhu má co největší obsah. Vypočítej obsah tohoto trojúhelníku.
Do kruhu s průměrem 20cm byl vepsán pravoúhlý trojúhelník, jehož přepona je průměrem kruhu má co největší obsah. Vypočítej obsah tohoto trojúhelníku. - Hliníkový 3
 Hliníkový kotouč má průměr 96mm. Z tabule plechu 1m dlouhé a 10cm široké se vyseká 10 kotoučů. Kolik % je odpad?
Hliníkový kotouč má průměr 96mm. Z tabule plechu 1m dlouhé a 10cm široké se vyseká 10 kotoučů. Kolik % je odpad? - Sestroj 21
 Sestroj rovnoběžník ABCD: AB=4,8cm, va=3cm, BC =4cm. Vypočítejte obvod. Proveďte náčrtek.
Sestroj rovnoběžník ABCD: AB=4,8cm, va=3cm, BC =4cm. Vypočítejte obvod. Proveďte náčrtek. - Jak velká
 Jak velká je hnědě vybarvená plocha uvnitř čtverce o straně 6 cm, pokud každá ze čtyř hnědých kruhových úsečí je z kruhu o poloměru délky stany čtverce? Délka kruhových úsečí je rovna délce strany čtverce. Situace je vyobrazena na obrázku vpravo.
Jak velká je hnědě vybarvená plocha uvnitř čtverce o straně 6 cm, pokud každá ze čtyř hnědých kruhových úsečí je z kruhu o poloměru délky stany čtverce? Délka kruhových úsečí je rovna délce strany čtverce. Situace je vyobrazena na obrázku vpravo.
