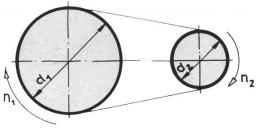
Klínový řemen
Vypočítejte délku klínového řemene pokud průměr řemenic je:
d1 = 600mm
d2 = 120mm
d = 480mm (vzdálenost os řemenic)
d1 = 600mm
d2 = 120mm
d = 480mm (vzdálenost os řemenic)
Správná odpověď:
Zobrazuji 6 komentářů:
Žák
Výše uvedené řešení vychází z chybného předpokladu, že tečna obou kružnic má stejný sklon ke spojnici středů řemenic jako spojnice průsečíků svislic procházejících středy s kružnicemi. Jinými slovy tečna není rovnoběžná s úsečkou ve výpočtu označenou jako "b". Pochopitelně je tedy chybně určen i úhel "A".
Dr Math
uhel A je uhel tecny vzhledem k spojnici stredu. body dotyku a stredy kruznic S1,S2 formuji pravouhlej lichobeznik, ktery lze rozlozit na obdelnik a pravouhly trojuhelnik. Pravouhlej trojuhelnik ma take uhel A, stranu d = |S1S2| a stranu r1-r2. Tecna je rovnobezna s useckou "b" (dlzka rovne casti remene)...
Proc by take nebyla, kdyz v bodech dotyku je tecna kolma na r1 ale take na r2, tudiz formuje se tam obdelnik o stranach b a r1.
Dejte padnejsi argument.
Proc by take nebyla, kdyz v bodech dotyku je tecna kolma na r1 ale take na r2, tudiz formuje se tam obdelnik o stranach b a r1.
Dejte padnejsi argument.
Dr Math
fuu to dalo namahu nakreslit to. Nicmene nechapu zloute primke s, a aj jinym zlutym primkam. Nemaji zaden smysl. Dulezity je jeno pravouhlej lichobeznik T1T2S2S1. tam je zrejme ze T1S1 je rovnobezne s T2S2. uhel fi = S2PT1 je proste stejny ako uhel spojnici středů řemenic jako spojnice průsečíků svislic procházejících středy s kružnicemi
Žák
No, měl jsem za to, že z obrázku v odkazu je zcela zřejmé, že tečna „t“, pochopitelně procházející body T1, T2, není rovnoběžná s přímkou „s” procházející průsečíky kružnic se svislicemi procházejícími středy. Důkazem budiž třeba to, pominuli již zmiňované analytické řešení, že v pravoúhlém trojúhelníku o stranách d, a, b = |T1T2|, z něhož správně počítáte velikost |T1T2|, musí být příslušný vnitřní úhel pí/6 rad nikoli 0,4636 rad.
Vít
No nevím, také mi to nějak nesedí. Výpočet a použití úhlu A je dost divné. Podle mne ty oblouky jsou 240° a 120°. A výsledek je tedy cca 2214 mm.
3 roky 1 Like
Tipy na související online kalkulačky
Chcete proměnit jednotku délky?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- geometrie
- podobnost trojúhelníků
- planimetrie
- pravoúhlý trojúhelník
- kruh, kružnice
- trojúhelník
- lichoběžník
- kruhová výseč
- kruhový oblouk
- goniometrie a trigonometrie
- sinus
- tangens
- arkussinus
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Z5–I–1 MO 2017
 Honzík dostal kapesné a chce si za něj koupit něco dobrého. Kdyby si koupil čtyři koláče. Zbylo by mu 5kč. Kdyby si chtěl koupit pět koláčů, chybělo by mu 6kč. Kdyby si koupil dva koláče a tři koblihy, utratil by celé kapesné beze zbytku. Kolik stoji jedn
Honzík dostal kapesné a chce si za něj koupit něco dobrého. Kdyby si koupil čtyři koláče. Zbylo by mu 5kč. Kdyby si chtěl koupit pět koláčů, chybělo by mu 6kč. Kdyby si koupil dva koláče a tři koblihy, utratil by celé kapesné beze zbytku. Kolik stoji jedn - Čtvercova sít
 Čtvercova síť se skladá ze čtverců se stranou delky 1cm. Narysujte do ní alespoň tři různe obrazce takové, aby každý měl obsah 6cm² a obvod 12cm a aby jejich strany splývaly s přímkami síťe.
Čtvercova síť se skladá ze čtverců se stranou delky 1cm. Narysujte do ní alespoň tři různe obrazce takové, aby každý měl obsah 6cm² a obvod 12cm a aby jejich strany splývaly s přímkami síťe. - Kroužek v škole
 27 žáků navštěvuje nějaký kroužek, taneční kroužek navštěvuje 14 žáků, sportovní 21 žáků a dramatický 16 žáků. Taneční a sportovní navštěvuje 9 žáků, taneční a dramatický 6 žáků, sportovní a dramatický 11 žáků. Kolik žáků navštěvuje všechny 3 kroužky?
27 žáků navštěvuje nějaký kroužek, taneční kroužek navštěvuje 14 žáků, sportovní 21 žáků a dramatický 16 žáků. Taneční a sportovní navštěvuje 9 žáků, taneční a dramatický 6 žáků, sportovní a dramatický 11 žáků. Kolik žáků navštěvuje všechny 3 kroužky? - Desátém 3034
 Urči, kolik malin je ve třetím a v desátém košíku, pokud v prvním jsou 3 maliny a v každém dalším je o 8 malin více
Urči, kolik malin je ve třetím a v desátém košíku, pokud v prvním jsou 3 maliny a v každém dalším je o 8 malin více
- Centy
 Julka má o 3 centy více než Hugo. Celkem maji 27 centů. Kolik centů má Julka a kolik Hugo?
Julka má o 3 centy více než Hugo. Celkem maji 27 centů. Kolik centů má Julka a kolik Hugo? - Peníze a obchod
 Peter zaplatil v obchodě o 3 eura více, než je polovina částky, kterou měl při příchodu do obchodu. Při odchodu mu zůstalo 10 eur. Kolik eur měl při příchodu do obchodu?
Peter zaplatil v obchodě o 3 eura více, než je polovina částky, kterou měl při příchodu do obchodu. Při odchodu mu zůstalo 10 eur. Kolik eur měl při příchodu do obchodu? - Lentilka
 Lentilka udělala 31 palačinek. 8 nenaplnila ničím, 14 palačinek naplnila jahodovým džemem, 16 naplnila tvarohem. a) Kolik udělala Lentilka jahodovo-tvarohových palačinek? Maksík snědl 4 jahodovo-tvarohové a všechny čistě jahodové palačinky. Mikulaš snědl
Lentilka udělala 31 palačinek. 8 nenaplnila ničím, 14 palačinek naplnila jahodovým džemem, 16 naplnila tvarohem. a) Kolik udělala Lentilka jahodovo-tvarohových palačinek? Maksík snědl 4 jahodovo-tvarohové a všechny čistě jahodové palačinky. Mikulaš snědl - Králici
 V králíkárně je 48 strakatých králíků. Hnědých je o 23 méně než strakatých a bílých je 8-krát méně než strakatých. Kolik je v králíkárně králíků?
V králíkárně je 48 strakatých králíků. Hnědých je o 23 méně než strakatých a bílých je 8-krát méně než strakatých. Kolik je v králíkárně králíků? - Úsečky
 Úsečky délek 91 cm a 9,3 dm máme rozdělit na stejné díly tak, aby jejich délka v centimetrech byla vyjádřena celým číslem. Kolika způsoby je můžeme dělit?
Úsečky délek 91 cm a 9,3 dm máme rozdělit na stejné díly tak, aby jejich délka v centimetrech byla vyjádřena celým číslem. Kolika způsoby je můžeme dělit?
- Krkavci
 V pohádce o sedmero krkavcích bylo sedm bratrů, z nichž každý se narodil přesně o 2,0 roků po předchozím. Když byl nejstarší z bratrů právě 7-krát starší než nejmladší matka všechny zaklela. Kolik let bylo sedmero bratrům krkavcům, když je jejich matka za
V pohádce o sedmero krkavcích bylo sedm bratrů, z nichž každý se narodil přesně o 2,0 roků po předchozím. Když byl nejstarší z bratrů právě 7-krát starší než nejmladší matka všechny zaklela. Kolik let bylo sedmero bratrům krkavcům, když je jejich matka za - Čísla
 Určete počet všech přirozených čísel menších než 4961627, pokud každé je současně dělitelné 13, 2, 29. Jaký je jejich součet?
Určete počet všech přirozených čísel menších než 4961627, pokud každé je současně dělitelné 13, 2, 29. Jaký je jejich součet? - Převod
 Dvě ozubená kola, zapadající do sebe, mají převod 2:5. Středy odidvoch kol jsou od sebe vzdáleny 65 cm. Jaké poloměry mají kola?
Dvě ozubená kola, zapadající do sebe, mají převod 2:5. Středy odidvoch kol jsou od sebe vzdáleny 65 cm. Jaké poloměry mají kola? - Opice
 Do studny hluboké 32 metrů spadla opice. Každý den se jí daří vyškrábat se 3 metry, v noci však spadne zpět o 2 metry. Na který den se opice dostane ze studny?
Do studny hluboké 32 metrů spadla opice. Každý den se jí daří vyškrábat se 3 metry, v noci však spadne zpět o 2 metry. Na který den se opice dostane ze studny? - Z5–I–4 MO 2018
 V klubovně byly jen židle a stůl. Každá židle měla čtyři nohy, stůl byl trojnohý. Do klubovny přišli skauti. Každý si sedl na svou židli, dvě židle zůstaly neobsazené a počet nohou v místnosti byl 101. Kolik židlí bylo v klubovně?
V klubovně byly jen židle a stůl. Každá židle měla čtyři nohy, stůl byl trojnohý. Do klubovny přišli skauti. Každý si sedl na svou židli, dvě židle zůstaly neobsazené a počet nohou v místnosti byl 101. Kolik židlí bylo v klubovně?
- Obdélníky
 Vystřihl jsem si dva obdélníky s obsahy 54 cm², 90 cm². Jejich strany jsou vyjádřené celými čísly v centimetrech. Pokud tyto obdélníky přiložím k sobě, dostanu obdélník s obsahem 144 cm². Jaké rozměry může mít tento velký obdélník? Napiš všechny možnosti.
Vystřihl jsem si dva obdélníky s obsahy 54 cm², 90 cm². Jejich strany jsou vyjádřené celými čísly v centimetrech. Pokud tyto obdélníky přiložím k sobě, dostanu obdélník s obsahem 144 cm². Jaké rozměry může mít tento velký obdélník? Napiš všechny možnosti. - Narozeninám 6277
 Peter dostal k narozeninám nové kolo. Jeho kolo bylo vybaveno mnoha převody. Kolik má Peter možností k nastavení převodu, má-li vpředu 3 kolečka a vzadu 8 koleček? Vypiš všechny
Peter dostal k narozeninám nové kolo. Jeho kolo bylo vybaveno mnoha převody. Kolik má Peter možností k nastavení převodu, má-li vpředu 3 kolečka a vzadu 8 koleček? Vypiš všechny - Čtvercová 6040
 Na obrázku je čtvercová síť ve které má strana jednoho čtverce délku 1 cm. Narýsuj obdélník o obsahu 18 čtverců, který má obvod 22 cm.
Na obrázku je čtvercová síť ve které má strana jednoho čtverce délku 1 cm. Narýsuj obdélník o obsahu 18 čtverců, který má obvod 22 cm.
