Dvě koule
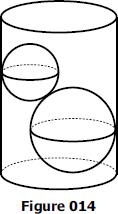
Dvě koule, jedna s poloměrem 8 cm a další s poloměrem 6 cm, se vloži do válcové plastové nádoby s poloměrem 10 cm. Najděte množství vody potřebné k jejich potopení.
Správná odpověď:
Zobrazuji 4 komentáře:
Žák
nechápu jak jste se dopracovali ke V=............................. předposlední řádek výpočtu
Www
no napr. x je vodorovna vzdalenost stredov gul. Je to logicke ak od priemeru valca (20 cm) odcitame po bokoch r a R. h je zvisla vzdalenost stredov gul. To je cista Pytagovoa veta. H je celkova vyska "vody" vo valci. Objemy su snad trivialne.... vzorec dosadis a mas...
Tipy na související online kalkulačky
Potřebujete pomoci sčítat, zkrátít či vynásobit zlomky? Zkuste naši zlomkovou kalkulačku.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- aritmetika
- odmocnina
- stereometrie
- válec
- koule
- tělesová úhlopříčka
- planimetrie
- Pythagorova věta
- pravoúhlý trojúhelník
- trojúhelník
- úhlopříčka
- čísla
- zlomky
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Pilíř 3
 Kolik betonu je třeba na vylití 8 betonových sloupů s podstavou čtverce: a = 38cm, výška sloupů je 6,2m? V každém sloupu je dutina válce o průměru 15cm.
Kolik betonu je třeba na vylití 8 betonových sloupů s podstavou čtverce: a = 38cm, výška sloupů je 6,2m? V každém sloupu je dutina válce o průměru 15cm. - Kolik 130
 Kolik hektolitrů vody je ve vodní nádrži tvaru válce s průměrem podstavy 3 metry a hloubkou 60cm?
Kolik hektolitrů vody je ve vodní nádrži tvaru válce s průměrem podstavy 3 metry a hloubkou 60cm? - Vnější
 Vnější obvod trubky je 32cm. Její délka je 60cm, hustota 8,5g/cm³ a hmotnost 9,495kg. Vypočítej tloušťku stěny trubky.
Vnější obvod trubky je 32cm. Její délka je 60cm, hustota 8,5g/cm³ a hmotnost 9,495kg. Vypočítej tloušťku stěny trubky. - Protilehlých 61594
 Vypočítejte, kolik procent objemu krychle představuje objem válce vepsaného do krychle. Podstavy válce jsou kruhy vepsané do dvou protilehlých stěn kostky s hranou a=14 cm.
Vypočítejte, kolik procent objemu krychle představuje objem válce vepsaného do krychle. Podstavy válce jsou kruhy vepsané do dvou protilehlých stěn kostky s hranou a=14 cm.
- Urči poloměr 3
 Urči poloměr a výšku (v centimetrech) rovnostranného válce, který má objem 1 litr.
Urči poloměr a výšku (v centimetrech) rovnostranného válce, který má objem 1 litr. - Vypočítejte radiátor
 Vypočítejte výkon radiátoru, pokud má tepelný spád (rozdíl teplot vstupní vody a zpátečky) a) 5°C b) 10°C c) 15°C d) 20°C a objemový průtok topné vody 45 kg/hod. Jak rychle proudí voda v přívodním potrubí k radiátoru e) DN16 a f) DN20? Označení DN je diam
Vypočítejte výkon radiátoru, pokud má tepelný spád (rozdíl teplot vstupní vody a zpátečky) a) 5°C b) 10°C c) 15°C d) 20°C a objemový průtok topné vody 45 kg/hod. Jak rychle proudí voda v přívodním potrubí k radiátoru e) DN16 a f) DN20? Označení DN je diam - Láhve piva
 Sud o objemu 3hl byl stočen do 375 láhví. Některé měly objem 0,7l, některé jeden litr. Kolik bylo kterých?
Sud o objemu 3hl byl stočen do 375 láhví. Některé měly objem 0,7l, některé jeden litr. Kolik bylo kterých? - Krychle 50
 Krychle ABCDEFGH má hranu délky 3 cm. Vypočítejte objem jehlanu ABCDH.
Krychle ABCDEFGH má hranu délky 3 cm. Vypočítejte objem jehlanu ABCDH. - Osový řez válce
 Osovým řezem válce je čtverec o obsahu 56,25 cm². Vypočítejte jeho povrch a objem. Výsledek vyjádřete ve čtverečných decimetrech a v krychlových decimetrech a zaokrouhlete na setiny.
Osovým řezem válce je čtverec o obsahu 56,25 cm². Vypočítejte jeho povrch a objem. Výsledek vyjádřete ve čtverečných decimetrech a v krychlových decimetrech a zaokrouhlete na setiny.
- Katka 7
 Katka si objednala dort ve tvaru valce o objemu 15,7l. Skládá se ze dvou pater. Objem horního patra je 4x menší než objem dolního patra. Výška obou pater stejna a je rovná polomeru horního patra dortu. Katka rozkrojila dort kolmo k podložce na 2 stejně čá
Katka si objednala dort ve tvaru valce o objemu 15,7l. Skládá se ze dvou pater. Objem horního patra je 4x menší než objem dolního patra. Výška obou pater stejna a je rovná polomeru horního patra dortu. Katka rozkrojila dort kolmo k podložce na 2 stejně čá - Plášť válce 3
 Obsah pláště rotačního válce je třikrát větší než obsah jedné podstavy tohoto válce. Poloměr podstavy válce je 10 cm. Jaký je povrch válce?
Obsah pláště rotačního válce je třikrát větší než obsah jedné podstavy tohoto válce. Poloměr podstavy válce je 10 cm. Jaký je povrch válce? - Prosím 6
 Prosím o vyjádření r ze vzorce pro povrch válce.
Prosím o vyjádření r ze vzorce pro povrch válce. - Válec 28
 Válec má povrch pláště 88 cm čtverečních a objem 176 cm krychlových. Vypočítejte poloměr, výšku a povrch uvedeného tělesa
Válec má povrch pláště 88 cm čtverečních a objem 176 cm krychlových. Vypočítejte poloměr, výšku a povrch uvedeného tělesa - Jaký je 7
 Jaký je objem válce o poloměru 11,3 cm a výšce 28 cm?, děkuji.
Jaký je objem válce o poloměru 11,3 cm a výšce 28 cm?, děkuji.
- Drát
 Kolik metrů měděného drátu o průměru d=3 mm se vyrobí ze 60 kg měděného sběru, když měrná hmotnost mědi je p=9g/cm³?
Kolik metrů měděného drátu o průměru d=3 mm se vyrobí ze 60 kg měděného sběru, když měrná hmotnost mědi je p=9g/cm³? - Na plášti
 Na plášti válce je nakreslena pravidelná šroubovice taková, že se přesně třikrát ovine kolem válce (tedy bod, kde se dotýká horní podstavy, je přesně nad bodem, kde se dotýká dolní podstavy). Je-li průměr válce roven 2 a jeho výška má velikost 3, pak délk
Na plášti válce je nakreslena pravidelná šroubovice taková, že se přesně třikrát ovine kolem válce (tedy bod, kde se dotýká horní podstavy, je přesně nad bodem, kde se dotýká dolní podstavy). Je-li průměr válce roven 2 a jeho výška má velikost 3, pak délk - Spádnice
 Určit objem a povrch kužele, jehož spádnice o délce 8cm svírá s rovinou podstavy úhel 75 stupňů
Určit objem a povrch kužele, jehož spádnice o délce 8cm svírá s rovinou podstavy úhel 75 stupňů
