Šesťuholník nepravidelný
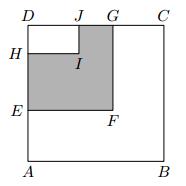
Na obrázku je štvorec ABCD, štvorec EFGD a obdĺžnik HIJD. Body J a G ležia na strane CD, pričom platí |DJ| < |DG| a body H a E ležia na strane DA, pričom platí /DH/ < /DE/. Ďalej vieme, že/DJ/ = /GC/. Šesťuholník ABCGFE má obvod 96 cm, šesťuholník EFGJIH má obvod 60 cm a obdĺžnik HIJD má obvod 28 cm. Určte obsah šesťuholníka EFGJIH.
Správna odpoveď:
Zobrazujem 1 komentár:
Mo-radce
Nápoveda. Dokážete určiť dĺžku niektoré úsečky, bez toho aby ste k tomu použili viac ako jeden zadaný rozmer?
Riešenie.
Zistíme rozmery štvorca EFGD a obdĺžnika HIJD, aby sme stanovili ich obsahy. Rozdiel týchto obsahov predstavuje žiadaný obsah šesťuholníka EFGJIH. Zadaný obvod šesťuholníka EFGJIH je rovný obvodu štvorca EFGD, lebo |JU| = |DH| a |HI| = |DJ|. Strana GD má teda veľkosť 60:4 = 15 (cm). Podobne zadaný obvod šesťuholníka ABCGFE je rovný obvodu štvorca ABCD, veľkosť strany CD je teda 96:4 = 24 (cm). Rozdiel dĺžok strán týchto dvoch štvorcov je rovný dĺžke úsečky GC, ktorá je podľa zadania rovná dĺžke úsečky DJ:
|DJ| = |GC| = 24 - 15 = 9 (cm).
Pomocou známeho obvodu obdĺžnika HIJD a dĺžky strany DJ stanovíme aj druhý rozmer tohto obdĺžnika:
|JI| = (28 - 2 · 9): 2 = 5 (cm).
Teraz máme všetky údaje potrebné na stanovenie obsahov štvorca EF GD a obdĺžnika HIJD:
S (EFGD) = 15 · 15 = 225 cm2
S (HIJD) = 9 · 5 = 45 cm2
Hľadaný obsah šesťuholníka teda je S (EFGJIH) = 225 - 45 = 180 cm2.
Riešenie.
Zistíme rozmery štvorca EFGD a obdĺžnika HIJD, aby sme stanovili ich obsahy. Rozdiel týchto obsahov predstavuje žiadaný obsah šesťuholníka EFGJIH. Zadaný obvod šesťuholníka EFGJIH je rovný obvodu štvorca EFGD, lebo |JU| = |DH| a |HI| = |DJ|. Strana GD má teda veľkosť 60:4 = 15 (cm). Podobne zadaný obvod šesťuholníka ABCGFE je rovný obvodu štvorca ABCD, veľkosť strany CD je teda 96:4 = 24 (cm). Rozdiel dĺžok strán týchto dvoch štvorcov je rovný dĺžke úsečky GC, ktorá je podľa zadania rovná dĺžke úsečky DJ:
|DJ| = |GC| = 24 - 15 = 9 (cm).
Pomocou známeho obvodu obdĺžnika HIJD a dĺžky strany DJ stanovíme aj druhý rozmer tohto obdĺžnika:
|JI| = (28 - 2 · 9): 2 = 5 (cm).
Teraz máme všetky údaje potrebné na stanovenie obsahov štvorca EF GD a obdĺžnika HIJD:
S (EFGD) = 15 · 15 = 225 cm2
S (HIJD) = 9 · 5 = 45 cm2
Hľadaný obsah šesťuholníka teda je S (EFGJIH) = 225 - 45 = 180 cm2.
8 rokov 1 Like
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Jednotky fyzikálnych veličín:
Téma:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Trojuholník MO Z8-I-5
 Trojuholník ABC je rozdelený úsečkami. Úsečky DE a AB sú rovnobežné. Trojuholníky CDH, CHI, CIE, FIH majú rovnaký obsah a to 8 dm². Zistite obsah štvoruholníka AFHD.
Trojuholník ABC je rozdelený úsečkami. Úsečky DE a AB sú rovnobežné. Trojuholníky CDH, CHI, CIE, FIH majú rovnaký obsah a to 8 dm². Zistite obsah štvoruholníka AFHD. - Súčet 50
 Súčet dĺžok všetkých hrán pravidelného štvorstenu ABCD je 48cm. Koľko cm má úsečka XY, ak viete, že X je stred AB a Y je stred CD?
Súčet dĺžok všetkých hrán pravidelného štvorstenu ABCD je 48cm. Koľko cm má úsečka XY, ak viete, že X je stred AB a Y je stred CD? - Trojuholníkov 79804
 Kolmý šesťboký hranol bol vytvorený opracovaním kocky o hrane dĺžky 8 cm. Podstava hranola vznikne zo štvorcovej steny pôvodnej kocky oddelením 4 zhodných pravouhlých trojuholníkov s odvesnami dĺžok 3cm a 4cm. Výška hranola je 8 cm. Aký je objem šesťiboké
Kolmý šesťboký hranol bol vytvorený opracovaním kocky o hrane dĺžky 8 cm. Podstava hranola vznikne zo štvorcovej steny pôvodnej kocky oddelením 4 zhodných pravouhlých trojuholníkov s odvesnami dĺžok 3cm a 4cm. Výška hranola je 8 cm. Aký je objem šesťiboké - Urč veľkosť
 Urč veľkosť uhla ACF v pravidelnom 6-uholníku ABCDEF.
Urč veľkosť uhla ACF v pravidelnom 6-uholníku ABCDEF.
- Zostrojte 11
 Zostrojte štvoruholník ABCD, ak AB=10cm, AD=6cm, DC=6,5cm a uhol BCD=90 stupňov
Zostrojte štvoruholník ABCD, ak AB=10cm, AD=6cm, DC=6,5cm a uhol BCD=90 stupňov - Obvod 48
 Obvod pravidelného osemuholníka je 8u + 16 cm. Vypočítajte stranu, ak u = 0,5 cm.
Obvod pravidelného osemuholníka je 8u + 16 cm. Vypočítajte stranu, ak u = 0,5 cm. - Pravidelný 12
 Pravidelný šesťboký hranol je vysoký 2 cm. Polomer kružnice opísanej podstave je 8 cm. Určte jeho objem a povrch.
Pravidelný šesťboký hranol je vysoký 2 cm. Polomer kružnice opísanej podstave je 8 cm. Určte jeho objem a povrch. - Vypočítaj 85
 Vypočítaj povrch pravidelného jedenásťbokého hranola, ak obsah jeho podstavy je 58cm2, hrana podstavy je dlhá 6cm, výška hranola je 21cm
Vypočítaj povrch pravidelného jedenásťbokého hranola, ak obsah jeho podstavy je 58cm2, hrana podstavy je dlhá 6cm, výška hranola je 21cm - Vypočítajte 30
 Vypočítajte objem nádoby tvaru šesťbokého hranola vysokého 1,4 m, ktorého obsah podstavy je 8300 cm².
Vypočítajte objem nádoby tvaru šesťbokého hranola vysokého 1,4 m, ktorého obsah podstavy je 8300 cm².
- Rovnostranného 30951
 Narysuj päťuholník ABCDE ktory sa skladá z štvorca ABCE o strane 44mm a rovnostranného trojuholníka CDE. Vďaka za pomoc.
Narysuj päťuholník ABCDE ktory sa skladá z štvorca ABCE o strane 44mm a rovnostranného trojuholníka CDE. Vďaka za pomoc. - Hexa kváder
 Vypočítaj objem a povrch pravidelného šesťbokého hranola s hranou podstavy a=6cm s príslušnou výškou v1=5,2cm a výškou hranola h = 1 dm .
Vypočítaj objem a povrch pravidelného šesťbokého hranola s hranou podstavy a=6cm s príslušnou výškou v1=5,2cm a výškou hranola h = 1 dm . - Daný je 3
 Daný je pravidelný šesťuholník ABCDEF. Bod A má súradnice [1;3] a bod D má súradnice [4;7]. Vypočítajte súčet súradníc stredu jeho opísanej kružnice.
Daný je pravidelný šesťuholník ABCDEF. Bod A má súradnice [1;3] a bod D má súradnice [4;7]. Vypočítajte súčet súradníc stredu jeho opísanej kružnice. - Mravec 2
 Mravec sa pozerá v 45 stupňovom uhle na špičku stromu, od stromu je vzdialený 15 m, Aký je vysoký strom?
Mravec sa pozerá v 45 stupňovom uhle na špičku stromu, od stromu je vzdialený 15 m, Aký je vysoký strom? - Päťuholník nepravidelný
 Pruh papiera v tvare obdĺžnika s rozmermi 16 x 4 cm je preložený po dĺžke tak, že pravý spodný roh je priložený na ľavý horný roh. Akú plochu má vzniknutý päťuholník?
Pruh papiera v tvare obdĺžnika s rozmermi 16 x 4 cm je preložený po dĺžke tak, že pravý spodný roh je priložený na ľavý horný roh. Akú plochu má vzniknutý päťuholník?
- Sedem 8
 Sedem dvanástin okien na zámku je v tvare n-uholníka. Z týchto okien je šesť štrnástin v tvare štvoruholníka, pričom dve devätiny z nich tvoria okna štvorcové. Koľko okien je na zámku, ak štvorcových okien je 15?
Sedem dvanástin okien na zámku je v tvare n-uholníka. Z týchto okien je šesť štrnástin v tvare štvoruholníka, pričom dve devätiny z nich tvoria okna štvorcové. Koľko okien je na zámku, ak štvorcových okien je 15? - Pravidelného 7290
 Vypočítaj obsah pravidelného šesťuholníka, ak je polomer kružnice jemu opísanej 6,8 cm.
Vypočítaj obsah pravidelného šesťuholníka, ak je polomer kružnice jemu opísanej 6,8 cm. - Z7–I–2 MO 2018
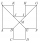 V dvanásťuholníku ABCDEFGHIJKL sú každé dve susedné strany navzájom kolmé a všetky strany s výnimkou strán AL a GF sú navzájom zhodné. Strany AL a GF sú oproti ostatným stranám dvojnásobne dlhé. Úsečky BG a EL sa pretínajú v bode M. Štvoruholník ABMJ má o
V dvanásťuholníku ABCDEFGHIJKL sú každé dve susedné strany navzájom kolmé a všetky strany s výnimkou strán AL a GF sú navzájom zhodné. Strany AL a GF sú oproti ostatným stranám dvojnásobne dlhé. Úsečky BG a EL sa pretínajú v bode M. Štvoruholník ABMJ má o
