Šesťuholník nepravidelný
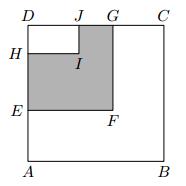
Na obrázku je štvorec ABCD, štvorec EFGD a obdĺžnik HIJD. Body J a G ležia na strane CD, pričom platí |DJ| < |DG| a body H a E ležia na strane DA, pričom platí /DH/ < /DE/. Ďalej vieme, že/DJ/ = /GC/. Šesťuholník ABCGFE má obvod 96 cm, šesťuholník EFGJIH má obvod 60 cm a obdĺžnik HIJD má obvod 28 cm. Určte obsah šesťuholníka EFGJIH.
Správna odpoveď:
Zobrazujem 1 komentár:
Mo-radce
Nápoveda. Dokážete určiť dĺžku niektoré úsečky, bez toho aby ste k tomu použili viac ako jeden zadaný rozmer?
Riešenie.
Zistíme rozmery štvorca EFGD a obdĺžnika HIJD, aby sme stanovili ich obsahy. Rozdiel týchto obsahov predstavuje žiadaný obsah šesťuholníka EFGJIH. Zadaný obvod šesťuholníka EFGJIH je rovný obvodu štvorca EFGD, lebo |JU| = |DH| a |HI| = |DJ|. Strana GD má teda veľkosť 60:4 = 15 (cm). Podobne zadaný obvod šesťuholníka ABCGFE je rovný obvodu štvorca ABCD, veľkosť strany CD je teda 96:4 = 24 (cm). Rozdiel dĺžok strán týchto dvoch štvorcov je rovný dĺžke úsečky GC, ktorá je podľa zadania rovná dĺžke úsečky DJ:
|DJ| = |GC| = 24 - 15 = 9 (cm).
Pomocou známeho obvodu obdĺžnika HIJD a dĺžky strany DJ stanovíme aj druhý rozmer tohto obdĺžnika:
|JI| = (28 - 2 · 9): 2 = 5 (cm).
Teraz máme všetky údaje potrebné na stanovenie obsahov štvorca EF GD a obdĺžnika HIJD:
S (EFGD) = 15 · 15 = 225 cm2
S (HIJD) = 9 · 5 = 45 cm2
Hľadaný obsah šesťuholníka teda je S (EFGJIH) = 225 - 45 = 180 cm2.
Riešenie.
Zistíme rozmery štvorca EFGD a obdĺžnika HIJD, aby sme stanovili ich obsahy. Rozdiel týchto obsahov predstavuje žiadaný obsah šesťuholníka EFGJIH. Zadaný obvod šesťuholníka EFGJIH je rovný obvodu štvorca EFGD, lebo |JU| = |DH| a |HI| = |DJ|. Strana GD má teda veľkosť 60:4 = 15 (cm). Podobne zadaný obvod šesťuholníka ABCGFE je rovný obvodu štvorca ABCD, veľkosť strany CD je teda 96:4 = 24 (cm). Rozdiel dĺžok strán týchto dvoch štvorcov je rovný dĺžke úsečky GC, ktorá je podľa zadania rovná dĺžke úsečky DJ:
|DJ| = |GC| = 24 - 15 = 9 (cm).
Pomocou známeho obvodu obdĺžnika HIJD a dĺžky strany DJ stanovíme aj druhý rozmer tohto obdĺžnika:
|JI| = (28 - 2 · 9): 2 = 5 (cm).
Teraz máme všetky údaje potrebné na stanovenie obsahov štvorca EF GD a obdĺžnika HIJD:
S (EFGD) = 15 · 15 = 225 cm2
S (HIJD) = 9 · 5 = 45 cm2
Hľadaný obsah šesťuholníka teda je S (EFGJIH) = 225 - 45 = 180 cm2.
8 rokov 1 Like
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Jednotky fyzikálnych veličín:
Téma:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Nádoba - štvorsten
 Nádoba tvaru rotačného valca s polomerom podstavy 5 cm je naplnená vodou. O čo stúpne hladina vody v nádobe, ak do nej ponoríme pravidelný štvorsten s hranou 7cm.
Nádoba tvaru rotačného valca s polomerom podstavy 5 cm je naplnená vodou. O čo stúpne hladina vody v nádobe, ak do nej ponoríme pravidelný štvorsten s hranou 7cm. - Trojuholník MO Z8-I-5
 Trojuholník ABC je rozdelený úsečkami. Úsečky DE a AB sú rovnobežné. Trojuholníky CDH, CHI, CIE, FIH majú rovnaký obsah a to 8 dm². Zistite obsah štvoruholníka AFHD.
Trojuholník ABC je rozdelený úsečkami. Úsečky DE a AB sú rovnobežné. Trojuholníky CDH, CHI, CIE, FIH majú rovnaký obsah a to 8 dm². Zistite obsah štvoruholníka AFHD. - Súčet 50
 Súčet dĺžok všetkých hrán pravidelného štvorstenu ABCD je 48cm. Koľko cm má úsečka XY, ak viete, že X je stred AB a Y je stred CD?
Súčet dĺžok všetkých hrán pravidelného štvorstenu ABCD je 48cm. Koľko cm má úsečka XY, ak viete, že X je stred AB a Y je stred CD? - Body ABC
 Body ABC ležia na kružnici k(S, r) tak, že uhol pri B je tupý. Aký veľký musí byť uhol pri vrchole B štvoruholníka SCBA, aby bol tento uhol trikrát väčší ako vnútorný uhol ASC toho istého štvoruholníka?
Body ABC ležia na kružnici k(S, r) tak, že uhol pri B je tupý. Aký veľký musí byť uhol pri vrchole B štvoruholníka SCBA, aby bol tento uhol trikrát väčší ako vnútorný uhol ASC toho istého štvoruholníka?
- Mnohouholník strany
 Určte druh mnohouholníka, ak je počet všetkých uhlopriečok 90. (Zapíšte počet jeho strán)
Určte druh mnohouholníka, ak je počet všetkých uhlopriečok 90. (Zapíšte počet jeho strán) - Mnohouholnik 5
 V istom mnohouholniku platí, že pomer súčtu veľkosti jeho vnútorných uhlov a súčtu veľkosti k ním doplnkových uhlov je 2:5. Koľko vrcholov má tento mnohouholník?
V istom mnohouholniku platí, že pomer súčtu veľkosti jeho vnútorných uhlov a súčtu veľkosti k ním doplnkových uhlov je 2:5. Koľko vrcholov má tento mnohouholník? - Vypočítaj 81095
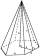 Šesťboký ihlan má obvod 120 cm, dĺžku bočnej hrany 25 cm. Vypočítaj jeho objem.
Šesťboký ihlan má obvod 120 cm, dĺžku bočnej hrany 25 cm. Vypočítaj jeho objem. - Kružnici
 Kružnici je opísaný a vpísaný pravidelný šesťuholník. Rozdiel ich obsahov je 8√3. Určte polomer kružnice.
Kružnici je opísaný a vpísaný pravidelný šesťuholník. Rozdiel ich obsahov je 8√3. Určte polomer kružnice. - Trojuholníkov 79804
 Kolmý šesťboký hranol bol vytvorený opracovaním kocky o hrane dĺžky 8 cm. Podstava hranola vznikne zo štvorcovej steny pôvodnej kocky oddelením 4 zhodných pravouhlých trojuholníkov s odvesnami dĺžok 3cm a 4cm. Výška hranola je 8 cm. Aký je objem šesťiboké
Kolmý šesťboký hranol bol vytvorený opracovaním kocky o hrane dĺžky 8 cm. Podstava hranola vznikne zo štvorcovej steny pôvodnej kocky oddelením 4 zhodných pravouhlých trojuholníkov s odvesnami dĺžok 3cm a 4cm. Výška hranola je 8 cm. Aký je objem šesťiboké
- Určte 9
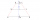 Určte vzdialenosť dvoch neprístupných miest P, Q, ak vzdialenosť dvoch pozorovacích miest A, B je 2000m a ak poznáte veľkosť uhlov QAB = 52°40'; PBA = 42°01'; PAB = 86°40' a QBA = 81°15'. Uvažované miesta A, B, P, Q ležia v jednej rovine.
Určte vzdialenosť dvoch neprístupných miest P, Q, ak vzdialenosť dvoch pozorovacích miest A, B je 2000m a ak poznáte veľkosť uhlov QAB = 52°40'; PBA = 42°01'; PAB = 86°40' a QBA = 81°15'. Uvažované miesta A, B, P, Q ležia v jednej rovine. - Urč veľkosť
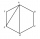 Urč veľkosť uhla ACF v pravidelnom 6-uholníku ABCDEF.
Urč veľkosť uhla ACF v pravidelnom 6-uholníku ABCDEF. - Zostrojte 11
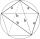 Zostrojte štvoruholník ABCD, ak AB=10cm, AD=6cm, DC=6,5cm a uhol BCD=90 stupňov
Zostrojte štvoruholník ABCD, ak AB=10cm, AD=6cm, DC=6,5cm a uhol BCD=90 stupňov - Štvoruholník ASBE
 Na obrázku je štvorec ABCD so stredom S a stranou dlhou 8 cm. Bod E je l'ubovoľný bod strany CD rozny od C a D. Vypočítajte obsah štvoruholníka ASBE v cm².
Na obrázku je štvorec ABCD so stredom S a stranou dlhou 8 cm. Bod E je l'ubovoľný bod strany CD rozny od C a D. Vypočítajte obsah štvoruholníka ASBE v cm². - Vypočítaj 335
 Vypočítaj objem vosku, z ktorého je vyrobená sviečka v tvare pravidelného šesťbokého ihlana s výškou 6,5 cm a dĺžkou hrany podstavy 3 cm.
Vypočítaj objem vosku, z ktorého je vyrobená sviečka v tvare pravidelného šesťbokého ihlana s výškou 6,5 cm a dĺžkou hrany podstavy 3 cm.
- Zo štvorca 2
 Zo štvorca o strane 4 cm odrežeme štyri pravouhlé rovnoramenné trojuholníky s pravým uhlom vo vrcholoch štvorca a s preponou √2 cm. Dostaneme osemuholník. Vypočítajte jeho obvod, ak plocha osemuholníka je 14cm².
Zo štvorca o strane 4 cm odrežeme štyri pravouhlé rovnoramenné trojuholníky s pravým uhlom vo vrcholoch štvorca a s preponou √2 cm. Dostaneme osemuholník. Vypočítajte jeho obvod, ak plocha osemuholníka je 14cm². - Pre súčet
 Pre súčet s veľkostí vnútorných uhlov mnohouholníka, kde n je počet jeho strán, platí vzťah s=(n−2)⋅180 stupňov. Koľko strán má mnohouholník, ak súčet veľkostí jeho vnútorných uhlov je 900°?
Pre súčet s veľkostí vnútorných uhlov mnohouholníka, kde n je počet jeho strán, platí vzťah s=(n−2)⋅180 stupňov. Koľko strán má mnohouholník, ak súčet veľkostí jeho vnútorných uhlov je 900°? - Obvod 48
 Obvod pravidelného osemuholníka je 8u + 16 cm. Vypočítajte stranu, ak u = 0,5 cm.
Obvod pravidelného osemuholníka je 8u + 16 cm. Vypočítajte stranu, ak u = 0,5 cm.
