Z7-1-6 MO 2018
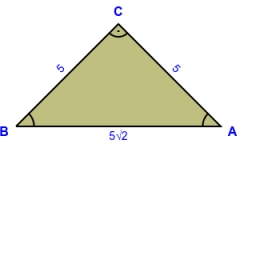
Daný je rovnoramenný pravouhlý trojuholník ABS so základňou AB. Na kružnici, ktorá má stred v bode S a prechádza bodmi A a B, leží bod C tak, že trojuholník ABC je rovnoramenný.
Určte, koľko bodov C vyhovuje uvedeným podmienkam, a všetky také body zostrojte.
Určte, koľko bodov C vyhovuje uvedeným podmienkam, a všetky také body zostrojte.
Správna odpoveď:
Zobrazujem 4 komentáre:
Dr Math
.. .dva vrcholy C lezia na priamke iducej bodom S a stredom strany AB prienik dana kruznica k
... dva lezia na prieniku kruznic zostrojenej v strede k1(A,r=|AB|), a danej kruznice k a kruznice k2(B,r=|AB|) s danou kruznicou k
... dva lezia na prieniku kruznic zostrojenej v strede k1(A,r=|AB|), a danej kruznice k a kruznice k2(B,r=|AB|) s danou kruznicou k
Žiak
Ak je dané, že bod C leží na tej istej kružnici ako body A a B, potom správna odpoveď by mala byť dva. Mýlim sa?
Dr Math
dalsie dva lezia tiez na tej kruznici iducej bodmi A a B, ale trojuholnik ma obe ramena dlzky a=|AB|... preto sa robia kruznice a bodu A a bodu B a prienik s tou povodnou.
Žiak
Ďakujem. Ja som sa sústredila iba na prienik nových kružníc (k1 a k2) a neuvedomila som si, že súčasne pretínajú aj pôvodnú kružnicu k. Až keď som si to nakreslila a ešte raz pozrela. Srdečná vďaka za pomoc.
5 rokov 1 Like
Tipy na súvisiace online kalkulačky
Vypočet rovnoramenného trojuholníka.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Jednotky fyzikálnych veličín:
Téma:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Jednotiek 68324
 Kruh je má stred v bode (-7, -1) a prechádza bodom (8, 7). Polomer kruhu je r jednotiek. Bod (-15, y) leží na tejto kružnici. Čo je r a y (alebo y1, y2)?
Kruh je má stred v bode (-7, -1) a prechádza bodom (8, 7). Polomer kruhu je r jednotiek. Bod (-15, y) leží na tejto kružnici. Čo je r a y (alebo y1, y2)? - Ostrouhlý trojuholník
 Daný je ostrouhlý trojuholník ABC. Na polpriamkach opačných k BA a CA ležia postupne body D a E tak, že |BD| = |AC| a |CE| = |AB|. Dokážte, že stred kružnice opísanej trojuholníku ADE leží na kružnici opísanej trojuholníku ABC.
Daný je ostrouhlý trojuholník ABC. Na polpriamkach opačných k BA a CA ležia postupne body D a E tak, že |BD| = |AC| a |CE| = |AB|. Dokážte, že stred kružnice opísanej trojuholníku ADE leží na kružnici opísanej trojuholníku ABC. - Trojuholník ABC
 V trojuholníku ABC so stranou BC dĺžky 2 cm je bod K stredom strany AB. Body L a M rozdeľujú stranu AC na tri zhodné úsečky. Trojuholník KLM je rovnoramenný s pravým uhlom pri vrchole K. Určte dĺžky strán AB, AC trojuholníka ABC.
V trojuholníku ABC so stranou BC dĺžky 2 cm je bod K stredom strany AB. Body L a M rozdeľujú stranu AC na tri zhodné úsečky. Trojuholník KLM je rovnoramenný s pravým uhlom pri vrchole K. Určte dĺžky strán AB, AC trojuholníka ABC. - Je daná
 Je daná kružnica k(S;2,5cm) a bod L ak |SL|=4cm. Zostrojte dotyčnicu ku kružnici, ktorá prechádza bodom L.
Je daná kružnica k(S;2,5cm) a bod L ak |SL|=4cm. Zostrojte dotyčnicu ku kružnici, ktorá prechádza bodom L.
- Trojuholník 72314
 Na obrázku je kružnica k so stredom S a polomerom 5 cm a bod A, ktorý je od stredu S vzdialený 13 cm. Z bodu A sú ku kružnici k zostrojenej dve dotyčnice p, q s bodmi dotyku P, Q. Okrem toho je ku kružnici k zostrojená ďalšia dotyčnica t, ktorá pretína do
Na obrázku je kružnica k so stredom S a polomerom 5 cm a bod A, ktorý je od stredu S vzdialený 13 cm. Z bodu A sú ku kružnici k zostrojenej dve dotyčnice p, q s bodmi dotyku P, Q. Okrem toho je ku kružnici k zostrojená ďalšia dotyčnica t, ktorá pretína do - Na kružnici
 Na kružnici s polomerom 10 cm a so stredom S sú dané body A, B, C tak, že stredový uhol ASB má 60 stupňov a stredový uhol ASC má 90 stupňov. Určte dĺžku oblúka kružnice a veľkosť posunutí AB a AC.
Na kružnici s polomerom 10 cm a so stredom S sú dané body A, B, C tak, že stredový uhol ASB má 60 stupňov a stredový uhol ASC má 90 stupňov. Určte dĺžku oblúka kružnice a veľkosť posunutí AB a AC. - Rovnoramenný - Z7–I–5
 Je daný trojuholník ABC so stranami /AB/ = 3 cm, /BC/ = 10 cm a uhlom ABC = 120°. Narysujte všetky body X tak, aby platilo, že trojuholník BCX je rovnoramenný a súčasne trojuholník ABX je rovnoramenný so základňou AB.
Je daný trojuholník ABC so stranami /AB/ = 3 cm, /BC/ = 10 cm a uhlom ABC = 120°. Narysujte všetky body X tak, aby platilo, že trojuholník BCX je rovnoramenný a súčasne trojuholník ABX je rovnoramenný so základňou AB. - Daný je 4
 Daný je štvorec ABCD. Na jeho uhlopriečke AC leží bod E tak, že platí vzdialenosť AB je rovná vzdialenosti AE. Aká je veľkosť uhla EBC?
Daný je štvorec ABCD. Na jeho uhlopriečke AC leží bod E tak, že platí vzdialenosť AB je rovná vzdialenosti AE. Aká je veľkosť uhla EBC? - Tetiva súradnice
 Je daná kružnica k so stredom v bode S = [0 ; 0] . Bod A = [40 ; 30] leží na kružnici k. Aká dlhá je tetiva BC ak stred P tejto tetivy má súradnice : [- 14 ; 0 ]?
Je daná kružnica k so stredom v bode S = [0 ; 0] . Bod A = [40 ; 30] leží na kružnici k. Aká dlhá je tetiva BC ak stred P tejto tetivy má súradnice : [- 14 ; 0 ]?
- Napíšte 5
 Napíšte všeobecnú rovnicu kružnice ktorámáv bode S(2;5)a bod B (5;6) leží na tejto kružnici.
Napíšte všeobecnú rovnicu kružnice ktorámáv bode S(2;5)a bod B (5;6) leží na tejto kružnici. - Rovnoramenný trojuholník
 Vypočítajte obsah a obvod rovnoramenného trojuholníka ABC so základňou AB, a = 6 cm, c = 7 cm.
Vypočítajte obsah a obvod rovnoramenného trojuholníka ABC so základňou AB, a = 6 cm, c = 7 cm. - Daný je 4
 Daný je rovnoramenný trojuholník so základňou 24dm a ramenom 15dm. Vypočítaj výšku trojuholníka.
Daný je rovnoramenný trojuholník so základňou 24dm a ramenom 15dm. Vypočítaj výšku trojuholníka. - V trojuholníku 15
 V trojuholníku ABC určte súradnice bodu B, ak viete, že body A, B ležia na priamke 3x-y-5=0, body A, C ležia na priamke 2x+3y+4=0, bod C leží na súradnicovej osi x a uhol pri vrchole C je pravý.
V trojuholníku ABC určte súradnice bodu B, ak viete, že body A, B ležia na priamke 3x-y-5=0, body A, C ležia na priamke 2x+3y+4=0, bod C leží na súradnicovej osi x a uhol pri vrchole C je pravý. - Rovnoramenný 82561
 Určite bod C tak, aby trojuholník ABC bol pravouhlý a rovnoramenný s preponou AB, kde A[4,-6], B[-2,10]
Určite bod C tak, aby trojuholník ABC bol pravouhlý a rovnoramenný s preponou AB, kde A[4,-6], B[-2,10]
- C-I-2 2018 MO
 Na strane AB trojuholníka ABC sú dané body D a E tak, že |AD| = |DE| = |EB|. Body A a B sú postupne stredmi úsečiek CF a CG. Priamka CD pretína priamku FB v bode I a priamka CE pretína priamku AG v bode J. Dokážte, že priesečník priamok AI a BJ leží na pr
Na strane AB trojuholníka ABC sú dané body D a E tak, že |AD| = |DE| = |EB|. Body A a B sú postupne stredmi úsečiek CF a CG. Priamka CD pretína priamku FB v bode I a priamka CE pretína priamku AG v bode J. Dokážte, že priesečník priamok AI a BJ leží na pr - MO Z9 2019 domáce kolo
 V trojuholníku ABC leží bod P v tretine úsečky AB (bližšie bodu A), bod R je v tretine úsečky PB (bližšie bodu P) a bod Q leží na úsečke BC tak, že uhly PCB a RQB sú zhodné. Určte pomer obsahov trojuholníkov ABC a PQC.
V trojuholníku ABC leží bod P v tretine úsečky AB (bližšie bodu A), bod R je v tretine úsečky PB (bližšie bodu P) a bod Q leží na úsečke BC tak, že uhly PCB a RQB sú zhodné. Určte pomer obsahov trojuholníkov ABC a PQC. - V rovnoramennom 4
 V rovnoramennom trojuholníku ABC so základňou AB; A[-3,4]; B[1,6] leží vrchol C na priamke 5x – 6y – 16 =0. Vypočítajte súradnice vrcholu C.
V rovnoramennom trojuholníku ABC so základňou AB; A[-3,4]; B[1,6] leží vrchol C na priamke 5x – 6y – 16 =0. Vypočítajte súradnice vrcholu C.
