Najmenší spoločný násobok (NSN) + matematická olympiáda - príklady a úlohy
Počet nájdených príkladov: 21
- Najmenšie z9 2022
 Nájdite najmenšie kladné čísla a a b, pre ktoré platia 7a³ = 11b⁵
Nájdite najmenšie kladné čísla a a b, pre ktoré platia 7a³ = 11b⁵ - Aritmetickú 80551
 Bolek a Lolek mali každý svoju aritmetickú postupnosť. Ako Lolek, tak Bolek postupnosť začínala číslom 2023 a končila číslom 3023. Tieto dve postupnosti mali 26 spoločných čísel. Pomer Bolkovej a Lolkovej diferencie bol 5:2. Aký rozdiel Bolkovej a Lolkove
Bolek a Lolek mali každý svoju aritmetickú postupnosť. Ako Lolek, tak Bolek postupnosť začínala číslom 2023 a končila číslom 3023. Tieto dve postupnosti mali 26 spoločných čísel. Pomer Bolkovej a Lolkovej diferencie bol 5:2. Aký rozdiel Bolkovej a Lolkove - Deti MO Z7 2021
 Súčin vekov všetkých detí pána Násobka je 1408. Vek najmladšieho dieťaťa je rovný polovici veku najstaršieho dieťaťa. Koľko detí má pán Násobok a koľko má rokov?
Súčin vekov všetkých detí pána Násobka je 1408. Vek najmladšieho dieťaťa je rovný polovici veku najstaršieho dieťaťa. Koľko detí má pán Násobok a koľko má rokov? - Slávkine čísla
 Slávka si napísala farebnými fixkami štyri rôzne prirodzené čísla: červené, modré, zelené a žlté. Keď červené číslo vydelí modrým, dostane ako neúplný podiel zelené číslo a žlté predstavuje zvyšok po tomto delení. Keď vydelí modré číslo zeleným, vyjde jej
Slávka si napísala farebnými fixkami štyri rôzne prirodzené čísla: červené, modré, zelené a žlté. Keď červené číslo vydelí modrým, dostane ako neúplný podiel zelené číslo a žlté predstavuje zvyšok po tomto delení. Keď vydelí modré číslo zeleným, vyjde jej
- Snehulienka 2019 MO Z7
 Snehulienka so siedmimi trpaslíkmi nazbierali šišky na táborák. Snehulienka povedala, že počet všetkých šišiek je číslo deliteľné dvoma. Prvý trpaslík prehlásil, že je to číslo deliteľné tromi, druhý trpaslík povedal, že je to číslo deliteľné štyrmi, tret
Snehulienka so siedmimi trpaslíkmi nazbierali šišky na táborák. Snehulienka povedala, že počet všetkých šišiek je číslo deliteľné dvoma. Prvý trpaslík prehlásil, že je to číslo deliteľné tromi, druhý trpaslík povedal, že je to číslo deliteľné štyrmi, tret - Matik - KSM
 V kuchárskej knihe od Mateja Matemakaka sa písalo: najväčší spoločný deliteľ gramáže múky a gramáže cukru je 15, najväčší spoločný deliteľ gramáže cukru a gramáže citrónovej kôry je 6, súčin gramáže cukru a gramáže citrónovej kôry je 1800, najmenší spoloč
V kuchárskej knihe od Mateja Matemakaka sa písalo: najväčší spoločný deliteľ gramáže múky a gramáže cukru je 15, najväčší spoločný deliteľ gramáže cukru a gramáže citrónovej kôry je 6, súčin gramáže cukru a gramáže citrónovej kôry je 1800, najmenší spoloč - MO Z8-I-2 2012
 Číslo X je najmenšie také prirodzené číslo, ktorého polovica je deliteľná tromi, tretina deliteľná štyrmi, štvrtina deliteľná jedenástimi a jeho polovica dáva zvyšok 5 po delení siedmimi. Nájdite toto číslo.
Číslo X je najmenšie také prirodzené číslo, ktorého polovica je deliteľná tromi, tretina deliteľná štyrmi, štvrtina deliteľná jedenástimi a jeho polovica dáva zvyšok 5 po delení siedmimi. Nájdite toto číslo. - MO C-I-3 2019
 Určte všetky dvojice prirodzených čísel A a B, pre ktoré platí, že súčet dvojnásobku najmenšieho spoločného násobku a trojnásobku najväčšieho spoločného deliteľa prirodzených čísel A a B je rovný ich súčinu.
Určte všetky dvojice prirodzených čísel A a B, pre ktoré platí, že súčet dvojnásobku najmenšieho spoločného násobku a trojnásobku najväčšieho spoločného deliteľa prirodzených čísel A a B je rovný ich súčinu. - Z7–I–5 MO 2018
 V záhradníctve Rose si jedna predajňa objednala celkom 120 ruží vo farbe červenej a žltej, druhá predajňa celkom 105 ruží vo farbe červenej a bielej a tretia predajňa celkom 45 ruží vo farbe žltej a bielej. Záhradníctvo zákazku splnilo, a to tak, že ruží
V záhradníctve Rose si jedna predajňa objednala celkom 120 ruží vo farbe červenej a žltej, druhá predajňa celkom 105 ruží vo farbe červenej a bielej a tretia predajňa celkom 45 ruží vo farbe žltej a bielej. Záhradníctvo zákazku splnilo, a to tak, že ruží
- MO C–I–1 2018
 Neznáme číslo je deliteľné práve štyrmi číslami z množiny {6, 15, 20, 21, 70}. Určite, ktorými.
Neznáme číslo je deliteľné práve štyrmi číslami z množiny {6, 15, 20, 21, 70}. Určite, ktorými. - Z7–I–4 2018 MO Betka
 Betka sa hrala s ozubenými kolesami, ktoré ukladala tak, ako je naznačené na obrázku. Keď potom zatočila jedným okolo, točili sa všetky ostatné. Nakoniec bola spokojná so súkolesím, pričom prvé koleso malo 32 a druhé 24 zubov. Keď sa tretie koleso otočilo
Betka sa hrala s ozubenými kolesami, ktoré ukladala tak, ako je naznačené na obrázku. Keď potom zatočila jedným okolo, točili sa všetky ostatné. Nakoniec bola spokojná so súkolesím, pričom prvé koleso malo 32 a druhé 24 zubov. Keď sa tretie koleso otočilo - Cukríky MO Z6-I-5 2017
 V plechovke boli červené a zelené cukríky. Cyril zjedol 2/5 všetkých červených cukríkov a Zuzka zjedla 3/5 všetkých zelených cukríkov. Teraz tvoria červené cukríky 3/8 všetkých cukríkov v plechovke. Koľko najmenej cukríkov mohlo byť pôvodne v plechovke?
V plechovke boli červené a zelené cukríky. Cyril zjedol 2/5 všetkých červených cukríkov a Zuzka zjedla 3/5 všetkých zelených cukríkov. Teraz tvoria červené cukríky 3/8 všetkých cukríkov v plechovke. Koľko najmenej cukríkov mohlo byť pôvodne v plechovke? - MO Z7–I–3 2017
 Zoologická záhrada ponúkala školským skupinám výhodné vstupné: každý piaty žiak dostáva vstupenku zdarma. Pán učiteľ 6.A spočítal, že ak kúpi vstupné deťom zo svojej triedy, ušetrí za štyri vstupenky a zaplatí 19,95 €. Pani učiteľka 6.B mu navrhla, nech k
Zoologická záhrada ponúkala školským skupinám výhodné vstupné: každý piaty žiak dostáva vstupenku zdarma. Pán učiteľ 6.A spočítal, že ak kúpi vstupné deťom zo svojej triedy, ušetrí za štyri vstupenky a zaplatí 19,95 €. Pani učiteľka 6.B mu navrhla, nech k - Nenastavoval 5414
 Matej zisťoval, ako presne meria vežové hodiny čas. Došiel k záveru, že keby ich nikto priebežne nenastavoval, ukazovali by úplne presný čas vždy raz za 200 dní. a) Vypočítaj, o koľko sekúnd sa čas meraný vežovými hodinami líši od presného času za 1 hodin
Matej zisťoval, ako presne meria vežové hodiny čas. Došiel k záveru, že keby ich nikto priebežne nenastavoval, ukazovali by úplne presný čas vždy raz za 200 dní. a) Vypočítaj, o koľko sekúnd sa čas meraný vežovými hodinami líši od presného času za 1 hodin
- MO Z8–I–3 - 2017 - Adelka
 Adelka mala na papieri napísané dve čísla. Keď k nim pripísala ešte ich najväčší spoločný deliteľ a najmenší spoločný násobok, dostala štyri rôzne čísla menšie ako 100. S úžasom zistila, že keď vydelí najväčšie z týchto štyroch čísel najmenším, dostane na
Adelka mala na papieri napísané dve čísla. Keď k nim pripísala ešte ich najväčší spoločný deliteľ a najmenší spoločný násobok, dostala štyri rôzne čísla menšie ako 100. S úžasom zistila, že keď vydelí najväčšie z týchto štyroch čísel najmenším, dostane na - MO Z9–I–3 - 2017
 Roboti Róbert a Hubert skladajú a rozoberajú mlynčeky na kávu. Pritom každý z nich mlynček zloží štyrikrát rýchlejšie, ako ho sám rozoberie. Keď ráno prišli do dielne, niekoľko mlynčekov už tam bolo zložených. O 7:00 začal Hubert skladať a Róbert rozobera
Roboti Róbert a Hubert skladajú a rozoberajú mlynčeky na kávu. Pritom každý z nich mlynček zloží štyrikrát rýchlejšie, ako ho sám rozoberie. Keď ráno prišli do dielne, niekoľko mlynčekov už tam bolo zložených. O 7:00 začal Hubert skladať a Róbert rozobera - Čokoláda 6
 Medzinárodná banda pašerákov čokolády vedená slávnym Jackom Krivým Nosom, ktorý má 7 spolupracovníkov, si vytipovalal bratislavské letisko ako križovatku svojich obchodov. Lietadlo z Bratislavy do Štokholmu lieta každý tretí deň. Lietadlo z Bratislavy do
Medzinárodná banda pašerákov čokolády vedená slávnym Jackom Krivým Nosom, ktorý má 7 spolupracovníkov, si vytipovalal bratislavské letisko ako križovatku svojich obchodov. Lietadlo z Bratislavy do Štokholmu lieta každý tretí deň. Lietadlo z Bratislavy do - Pyramída Z8–I–6
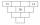 Každá tehlička zobrazenej pyramídy obsahuje jedno číslo. Kedykoľvek to je možné, je číslo v každej tehličke najmenším spoločným násobkom čísel z dvoch tehličiek ležiacich priamo nad ňou. Ktoré číslo môže byť v najspodnejšej tehličke? Určite všetky možnost
Každá tehlička zobrazenej pyramídy obsahuje jedno číslo. Kedykoľvek to je možné, je číslo v každej tehličke najmenším spoločným násobkom čísel z dvoch tehličiek ležiacich priamo nad ňou. Ktoré číslo môže byť v najspodnejšej tehličke? Určite všetky možnost - Stonožka
 Stonožka Mirka pozostáva z hlavy a niekoľkých článkov, na každom článku má jeden pár nôh. Keď sa ochladilo, rozhodla sa, že sa oblečie. preto si na treťom článku od konca a potom na každom ďalšom treťom článku obliekla ponožku na ľavú nôžku. Podobne si na
Stonožka Mirka pozostáva z hlavy a niekoľkých článkov, na každom článku má jeden pár nôh. Keď sa ochladilo, rozhodla sa, že sa oblečie. preto si na treťom článku od konca a potom na každom ďalšom treťom článku obliekla ponožku na ľavú nôžku. Podobne si na
Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať.
