Planimetria - slovné úlohy a príklady - strana 22 z 176
Počet nájdených príkladov: 3507
- Lichobežník KLMN 2
Lichobežník KLMN má základňu KL 40cm, MN 16cm. Na základni KL leží bod P. Úsečka NP rozdelí lichobežník na útvary o rovnakých obsahoch. Aká je vzdialenosť bodu P od bodu K? - Pexeso
Papier na kreslenie má rozmery 60cm a 840 mm. Žiaci ho majú rozdeliť na rovnako veľké štvorce, aby z nich mohli vyrobiť pexeso. Aký rozmer môžu štvorca mať, ak ich strana má byť väčší ako 3cm a menšia ako 10 cm? - Stolár Starý otec sa rozhodol vymeniť vrchnú dosku stola tvaru rovnoramenného lichobežníka s rozmermi základní 120 cm a 60 cm a rameno je dlhé 50 centimetrov. Koľko zaplatí za novú dosku ak jeden meter štvorcový stojí 17 eur?
- Rozmiestniť 6201
Pozemok pána Častky má rozmery 252 dm a 28 m. Ako najďalej od seba musia rozmiestniť koly na plot, aby boli po oboch stranách rovnako ďaleko? Koľko ich bude potrebovať na oplotenie celého pozemku? - Medzikružie 6
Na obrázku sú 2 sústredné kružnice. Tetiva väčšej kružnice s dĺžkou 10 cm je dotyčnicou menšej kružnice. Aký obsah má medzikružie? - Rovnoramenný lichobežník
Obvod rovnoramenného lichobežníka je 48 cm. Jedna strana je 2krát väčšia ako druhá. Určte rozmery lichobežníka. - Vypočítajte 31803
Anténny stožiar je 26 metrov vysoký. Je upevnený štyrmi oceľovými lanami zavesenými 1,6 metra pod najvyšším bodom stožiara a ukotvenými na zemi vo vrcholoch štvorca s dĺžkou strany 14 m. Stožiar je vztýčený v strede tohto štvorca. Vypočítajte celkovú dĺžk - Bambus
Bambus vysoký 32 stôp bol v určitej výške zlomený vetrom tak, že sa vrchol bambusu doktol zeme vo vzdialenosti 16 stôp od kmeňa. V akej výške od zeme bol bambus zlomený? - Terasa
Pán Novák chce vydláždiť terasu dlaždicami dvoch veľkostí, aby malých bolo rovnako veľa ako veľkých. Jeho terasa má tvar štvorca so stranou dlhou 3 metre. Z dvoch strán terasy je stena domu. Popri stene chce dať malé dlaždice, na zvyšok veľké. Chce len št - Mince
Paul mal našetrený určitý počet 2-eurových mincí. Mince si uložil v jednej vrstve do štvorca. Zostalo mu 4 mincí. Keď chcel zostaviť štvorec, ktorý by mal o jeden rad viac, chýbalo mu 15 mincí. Koľko eur mal? - Starkého záhrada
Starému otcovi ostal v záhrade voľný priestor v tvare pravouhlého trojuholníka s odvesnami dlhými 5 metrov a 12 metrov. Rozhodol sa ho rozdeliť na dve časti a to výškou na preponu. Na menšej časti vytvorí skalku, na väčšiu zaseje trávu. Koľko metrov štvor - Rybárska loď
Riešte graficky nasledujúcu úlohu. Rybárska loď vyšla z prístavu zavčas ráno a vydala sa severným smerom. Po 12 km plavby zmenila kurz a pokračovala 9 km na západ. Potom zakotvila a spustila siete. Ako ďaleko bola od miesta odchodu? - Záhrada
Chceme ohradiť obdĺžnikovú záhradu, ktorej pomer dĺžky a šírky je 2 : 1 a ktorej polovica obvodu hraničí s cestou. Cesta ohradenia pozdĺž cesty stojí 7 eur za meter ostatné ohradenie len 3 eurá za meter. Koľko árov má záhrada, ak jej ohradenie stojí 363 e - Kolesá traktora
Predné koleso traktora má obvod 18 dm a zadný 60 dm. Na najspodnejšej mieste obidvoch kolies urobíme červenú značku. Traktor sa rozbehne. V akej vzdialenosti od štartu sa opäť obe značky objavia zhodne dole? - Trojuholník PQR
V pravouhlom trojuholníku PQR je odvesna PQ rozdelená bodom X na dva úseky, z ktorých dlhší má dĺžku 25cm. Druhá odvesna PR má dĺžku 16 cm. Dĺžka prepony RX je 20 cm. Vypočítajte dĺžku p strany RQ. Výsledok zaokrúhli na 2 desatinné miesta. Jednotky "cm" - Tri oblúky
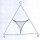V rovnostrannom trojuholníku o strane 2cm sú zakreslené oblúky troch kružníc so stredmi vo vrcholoch trojuholníka a polomery 1cm. Vypočítaj obsah vyšrafovanej časti - útvaru ktory tvori rozdiel medzi plochou trojuholníka a kruhovými výšok. - Okolo záhonu
Okolo obdĺžnikového záhonu s rozmermi 5,25 m a 7,5 m majú byť vysadené ruže rovnako ďaleko od seba tak, aby sa ruže nachádzali v každom rohu záhonu a spotrebovalo sa ich čo najmenej. a) V akej vzdialenosti ich vysadíme? b) Koľko ruží budete potrebovať? - Uhlopriečka štvorca
Vypočítajte dľžku uhlopriečky štvorca, ktorého strana je a=5 cm. - Pôvodného 8044
V danom obdĺžniku je dĺžka o 12 m väčšia ako šírka. Ak zmenšíme dĺžku o 10 m a šírku zväčšíme o 2 m dostaneme štvorec. Plošný obsah pôvodného obdĺžnika je o 300 m² väčší ako plošný obsah štvorca. Určite rozmery obdĺžnika. - Petrov obdĺžnik
Peter mal obdĺžnik šírky 2 cm a neznámej dĺžky. Radka mala obdĺžnik šírky 2 cm, ktorého dĺžka bola rovná obvodu Petrovho obdĺžnika. Keď k sebe obdĺžniky priložili ich šírkami, získali nový obdĺžnik s obvodom 63cm. Určte obsah Petrovho obdĺžnika.
Máš príklad, ktorý si tu nenašiel vyriešenú? Pošli nám tento príklad a my Ti ho skúsime vypočítať.
