Mám vrcholy
Mám vrcholy čtverce A/-3;1/a B/1;4/. Urči souřadnice vrcholů C a D, C' a D'. Díky Petr.
Správná odpověď:
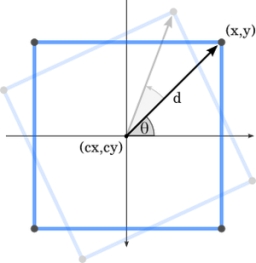
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Trojúhelníkový 81985
 Cvičenci stojí na značkách v řadách vzdálených od sebe přesně 1,5m. Tvoří rozšiřující se trojúhelníkový klín (v každé následující řadě je o jednoho cvičence více), přičemž vzdálenost čelního cvičence od zadní řady je 30m. Určete počet cvičenců.
Cvičenci stojí na značkách v řadách vzdálených od sebe přesně 1,5m. Tvoří rozšiřující se trojúhelníkový klín (v každé následující řadě je o jednoho cvičence více), přičemž vzdálenost čelního cvičence od zadní řady je 30m. Určete počet cvičenců. - Hlušice
 Hlušice a Jarošov jsou od sebe vzdáleny 10km. Z Hlušic vyjede koňský povoz do Jarošova rychlosti 5 km/h a zároveň z Jarošova do Hlušic vyrazí pocestný rychlosti 3 km/h. V momentě výjezdu povozu odstartuje z nosu koně moucha rychlostí 9 km/h a letí na nos
Hlušice a Jarošov jsou od sebe vzdáleny 10km. Z Hlušic vyjede koňský povoz do Jarošova rychlosti 5 km/h a zároveň z Jarošova do Hlušic vyrazí pocestný rychlosti 3 km/h. V momentě výjezdu povozu odstartuje z nosu koně moucha rychlostí 9 km/h a letí na nos - Hypotéka na dom
 Banka půjčí rodině 90 000 USD za roční úrokovou sazbu 4,5% na koupi domu. Rodina souhlasí se splácením půjčky měsíčními splátkami po dobu 15 let. Kolik by měla být měsíční splátka, aby se dluh splatil za 15 let?
Banka půjčí rodině 90 000 USD za roční úrokovou sazbu 4,5% na koupi domu. Rodina souhlasí se splácením půjčky měsíčními splátkami po dobu 15 let. Kolik by měla být měsíční splátka, aby se dluh splatil za 15 let? - 1!+2!+3!+ 34441
 Najděte zbytek po dělení, když dělíme součet 1!+2!+3!+. .. . . +300! číslem 13.
Najděte zbytek po dělení, když dělíme součet 1!+2!+3!+. .. . . +300! číslem 13.
- 5 členů
 Určete součet GP 30, 6, 1,2, jen prvních 5 členů. Jaký je součet všech členů (do nekonečna)?
Určete součet GP 30, 6, 1,2, jen prvních 5 členů. Jaký je součet všech členů (do nekonečna)? - Exponenciální pokles
 Nádrž obsahuje 55 litrů vody. Voda vytéká rychlostí 7% za minutu. Jak dlouho trvá vypuštění nádrže?
Nádrž obsahuje 55 litrů vody. Voda vytéká rychlostí 7% za minutu. Jak dlouho trvá vypuštění nádrže? - Cirkus 2
 Příjezd cirkusu do Plzně zaznamenal po ránu v 08:00 jeden občan města a tuto informaci předal 08:15 dalším třem obyvatelům města. Každý z těchto tři lidí pak v 08:30 informoval další tři obyvatele, tito pak opět v 08:45 předali zvěst o příjezdu cirkusu ka
Příjezd cirkusu do Plzně zaznamenal po ránu v 08:00 jeden občan města a tuto informaci předal 08:15 dalším třem obyvatelům města. Každý z těchto tři lidí pak v 08:30 informoval další tři obyvatele, tito pak opět v 08:45 předali zvěst o příjezdu cirkusu ka - Součet obsahů
 Nád výškou rovnostranného trojúhelníku ABC je sestrojen rovnostranný trojúhelník A1, B1, C1, nad jeho výškou je sestrojen rovnostranný trojúhelník A2, B2, C2, atd. Se postup neustále opakuje. Jaký je velký součet obsahů všech trojúhelníků, pokud strana tr
Nád výškou rovnostranného trojúhelníku ABC je sestrojen rovnostranný trojúhelník A1, B1, C1, nad jeho výškou je sestrojen rovnostranný trojúhelník A2, B2, C2, atd. Se postup neustále opakuje. Jaký je velký součet obsahů všech trojúhelníků, pokud strana tr - Adam a Eva - populace
 Kolik lidí bude na zemi ze dvou lidí za 5000 let, pokud se narodí každému páru vždy ve věku 25-35 let 4 děti, 2x chlapec a 2x dívka a každý člověk se dožije 75 let?
Kolik lidí bude na zemi ze dvou lidí za 5000 let, pokud se narodí každému páru vždy ve věku 25-35 let 4 děti, 2x chlapec a 2x dívka a každý člověk se dožije 75 let?
- V množině
 V množině N řešte danou rovnici: 1 – x + x² - x³ + x4 – x5 + …. + = 1/3
V množině N řešte danou rovnici: 1 – x + x² - x³ + x4 – x5 + …. + = 1/3 - Jednobuněčný organizmus
 Střevíčka (jednobuněčný organismus za ideálních podmínek se rozdělí na 2 střevíčky v průměru každých 27 hodin, Kdyby všechny střevíčky zůstává na živu, kolik by jich bylo za 7 dní?
Střevíčka (jednobuněčný organismus za ideálních podmínek se rozdělí na 2 střevíčky v průměru každých 27 hodin, Kdyby všechny střevíčky zůstává na živu, kolik by jich bylo za 7 dní? - 1/3+1/9+1/27+1/81 4113
 Určete součet nekonečné řady: 1/3+1/9+1/27+1/81.. .
Určete součet nekonečné řady: 1/3+1/9+1/27+1/81.. . - Nekonečný desetinný rozvoj
 Představ si nekonečné , desetinné číslo 0,99999999.. ... ... ... čili desetinnou čárku a za ní nekonečnou posloupnost devítek . Urči o kolik je toto číslo menší než číslo 1. Za vyřešení tohoto obtížného příkladu předem děkuji.
Představ si nekonečné , desetinné číslo 0,99999999.. ... ... ... čili desetinnou čárku a za ní nekonečnou posloupnost devítek . Urči o kolik je toto číslo menší než číslo 1. Za vyřešení tohoto obtížného příkladu předem děkuji. - Do kina
 Jitka se v 8 hod dozvěděla, že všech 1093 žáků školy půjde do kina. Během 20 min. to řekla 3 kamarádům. Každý z nich to opět za 20 min. řekl dalším třem. Tímto způsobem se zpráva šířila dál. V kolik hodin se ji dozvěděly všechny děti ve škole?
Jitka se v 8 hod dozvěděla, že všech 1093 žáků školy půjde do kina. Během 20 min. to řekla 3 kamarádům. Každý z nich to opět za 20 min. řekl dalším třem. Tímto způsobem se zpráva šířila dál. V kolik hodin se ji dozvěděly všechny děti ve škole?
- Zázračný strom
 Zázračný strom roste tak rychle, že se první den zvětší jeho výška o polovinu celkové výšky, druhý den o třetinu, třetí den o čtvrtinu, atd. Kolikrát se zvětší jeho výška za 6 dní?
Zázračný strom roste tak rychle, že se první den zvětší jeho výška o polovinu celkové výšky, druhý den o třetinu, třetí den o čtvrtinu, atd. Kolikrát se zvětší jeho výška za 6 dní? - Hod kostkami
 Když házíš deseti kostkami najednou, tak v průměru hodíš 35. Kolik průměrně hodíš, pokud vždy když padne šestka házíš tou kostkou znovu?
Když házíš deseti kostkami najednou, tak v průměru hodíš 35. Kolik průměrně hodíš, pokud vždy když padne šestka házíš tou kostkou znovu? - Šetření po centoch
 První den si odložím 1 cent a každý další o cent víc. Kolik si naspořit za rok (365 dní)?
První den si odložím 1 cent a každý další o cent víc. Kolik si naspořit za rok (365 dní)?
