PT - Přepona a výška
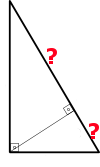
Pravoúhlý trojúhelník BTG má přeponu g = 117 m a výšku 54 m. Jak velké úseky vytíná výška na přeponu?
Správná odpověď:
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- V pravoúhlém 10
 V pravoúhlém trojúhelníku ABC jsou délky odvěsen a = 7,2 cm, b = 10,4 cm. Vypočtěte a) délky úseků přepony b) výšku k přeponě c
V pravoúhlém trojúhelníku ABC jsou délky odvěsen a = 7,2 cm, b = 10,4 cm. Vypočtěte a) délky úseků přepony b) výšku k přeponě c - Euklid 9
 Pomocí Euklidových vět a věty Pythagorovy doplňte následující parametry popisující pravoůhlý trojůhelník ABC s pravým úhlem při vrcholu C, pokud víme b=10, cb=8
Pomocí Euklidových vět a věty Pythagorovy doplňte následující parametry popisující pravoůhlý trojůhelník ABC s pravým úhlem při vrcholu C, pokud víme b=10, cb=8 - Vypočítejte 78874
 Daný je 4-úhelník ABCD vepsaný do kružnice, přičemž úhlopříčka AC je průměr kružnice. Vzdálenost bodu B od průměru je 15 cm, vzdálenost bodu D od průměru je 18 cm. Vypočítejte poloměr kružnice a obvod 4-úhelníku ABCD.
Daný je 4-úhelník ABCD vepsaný do kružnice, přičemž úhlopříčka AC je průměr kružnice. Vzdálenost bodu B od průměru je 15 cm, vzdálenost bodu D od průměru je 18 cm. Vypočítejte poloměr kružnice a obvod 4-úhelníku ABCD. - Trojúhelníku 72524
 Známe v pravoúhlém trojúhelníku výšku na přeponu vc = 4cm a přeponu c= 19cm. Jak vypočítat části strany - úseky na přeponě c1, c2
Známe v pravoúhlém trojúhelníku výšku na přeponu vc = 4cm a přeponu c= 19cm. Jak vypočítat části strany - úseky na přeponě c1, c2
- Euklidovy 61253
 Pomocí Euklidovy věty sestrojte úsečku o délce √15.
Pomocí Euklidovy věty sestrojte úsečku o délce √15. - Bod A
 Bod A má od kružnice o poloměru r = 4cm a středem S vzdálenost IA, kl = 10 cm. Vypočítejte: a) vzdálenost bodu A od bodu dotyku T, pokud je tečna ke kružnici vedena z bodu A b) vzdálenost dotykového bodu T od spojnice SA
Bod A má od kružnice o poloměru r = 4cm a středem S vzdálenost IA, kl = 10 cm. Vypočítejte: a) vzdálenost bodu A od bodu dotyku T, pokud je tečna ke kružnici vedena z bodu A b) vzdálenost dotykového bodu T od spojnice SA - MIT 1869
 Znáte délku částí 9 a 16, na které přeponu pravoúhlého trojúhelníku rozdělí kolmice spuštěná z jeho protilehlého vrcholu. Úkolem je zjistit délky stran trojúhelníku a délku úsečky x. Tato úloha byla součástí přijímacích zkoušek na Massachusettský technolo
Znáte délku částí 9 a 16, na které přeponu pravoúhlého trojúhelníku rozdělí kolmice spuštěná z jeho protilehlého vrcholu. Úkolem je zjistit délky stran trojúhelníku a délku úsečky x. Tato úloha byla součástí přijímacích zkoušek na Massachusettský technolo - Ak/AB/=5cm 47633
 Sestrojte čtverec, který má obsah jako kosodélník ABCD ak/AB/=5cm, /AD/=4cm a úhel |DAB|=30°
Sestrojte čtverec, který má obsah jako kosodélník ABCD ak/AB/=5cm, /AD/=4cm a úhel |DAB|=30° - Výška na stranu
 Pravoúhlý trojúhelník ABC má přeponu c dlouhou 9 cm a část přepony cb = 3 cm. Jak dlouhá je výška na stranu c?
Pravoúhlý trojúhelník ABC má přeponu c dlouhou 9 cm a část přepony cb = 3 cm. Jak dlouhá je výška na stranu c?
- Trojúhelník 32733
 Vypočítej pravoúhlý trojúhelník ABC, odvěsna b=43,5 cm přepona c=72,9 cm. Vypočítej cb, a, ca, v?
Vypočítej pravoúhlý trojúhelník ABC, odvěsna b=43,5 cm přepona c=72,9 cm. Vypočítej cb, a, ca, v? - Poměr odvěsen
 Pro délky odvěsen pravoúhlého trojúhelníku ABC platí a: b = 2:3. Přepona má délku 10 cm. Vypočtěte délky odvěsen toho trojúhelníku.
Pro délky odvěsen pravoúhlého trojúhelníku ABC platí a: b = 2:3. Přepona má délku 10 cm. Vypočtěte délky odvěsen toho trojúhelníku. - PT trojuhélnik
 Vypočtěte zbývající strany pravoúhlého trojúhelníku pokud známe b = 4 cm a vc = 2,4cm.
Vypočtěte zbývající strany pravoúhlého trojúhelníku pokud známe b = 4 cm a vc = 2,4cm. - V pravoúhlém 2
 V pravoúhlém trojúhelníku ABC jsou známy tyto prvky: a = 10 cm, vc = 9,23 cm. Vypočítejte o, R (poloměr opsané kružnice), r (poloměr vepsané kružnice).
V pravoúhlém trojúhelníku ABC jsou známy tyto prvky: a = 10 cm, vc = 9,23 cm. Vypočítejte o, R (poloměr opsané kružnice), r (poloměr vepsané kružnice). - V zahradě
 Starému otci zůstal v zahradě volný prostor ve tvaru pravoúhlého trojúhelníku s odvěsnami dlouhými 5 metrů a 12 metrů. Rozhodl se ho rozdělit na dvě části a to výškou na přeponu. Na menší části vytvoří skalku, na větší zaseje trávu. Kolik metrů čtverečníc
Starému otci zůstal v zahradě volný prostor ve tvaru pravoúhlého trojúhelníku s odvěsnami dlouhými 5 metrů a 12 metrů. Rozhodl se ho rozdělit na dvě části a to výškou na přeponu. Na menší části vytvoří skalku, na větší zaseje trávu. Kolik metrů čtverečníc
- Dvě těžnice
 Pravoúhlý trojúhelník, úhel C je 90 stupňů. Znám těžnici ta = 8 cm a těžnici tb = 12 cm. .. Jak spočítat délku stran?
Pravoúhlý trojúhelník, úhel C je 90 stupňů. Znám těžnici ta = 8 cm a těžnici tb = 12 cm. .. Jak spočítat délku stran? - RR trojuhelník
 Je dán rovnoramenný trojúhelník ABC, kde AB = AC. Obvod je 64 cm a výška na základnu je 24 cm. Najděte obsah tohoto rovnoramenného trojúhelníku
Je dán rovnoramenný trojúhelník ABC, kde AB = AC. Obvod je 64 cm a výška na základnu je 24 cm. Najděte obsah tohoto rovnoramenného trojúhelníku - Vypočítejte 20
 Vypočítejte strany pravoúhlého trojúhelníku, je-li zadána, že a+b=17cm, poloměr vepsané kružnice ρ=2cm.
Vypočítejte strany pravoúhlého trojúhelníku, je-li zadána, že a+b=17cm, poloměr vepsané kružnice ρ=2cm.
