Úhlopříčky
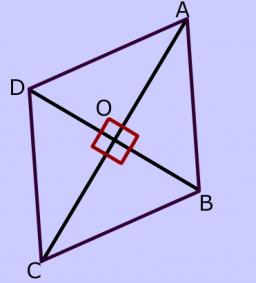
V kosočtverci je dáno a=160cm, alfa = 60 stupňů. Vypočtěte velikosti úhlopříček.
Správná odpověď:
Zobrazuji 2 komentáře:
Petr
cos je kosinus; jiste se to pocitat nejakou fintou typu rovnostranny trojuhelnik ma vsechny uhly 60 stupnu - cili aj jedna uhlopricka je u1=a=160 cm. Dale z pytagorovy vety a z faktu ze se uhlopricky rozpoluji plati:
a2 = (u1/2)2+(u2/2)2
a2 = a2/4+u22/4
3a2 = u22
u2 = a * sqrt(3) = 160* sqrt(3) = 277.12
Ale pro jine uhly jako 60 stupnu jedine cez sin a cosinus!
a2 = (u1/2)2+(u2/2)2
a2 = a2/4+u22/4
3a2 = u22
u2 = a * sqrt(3) = 160* sqrt(3) = 277.12
Ale pro jine uhly jako 60 stupnu jedine cez sin a cosinus!
Tipy na související online kalkulačky
Pythagorova věta je základ výpočtů kalkulačky pravouhlého trojuholníka.
Kosinovú větu přímo používá kalkulačka SUS trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Kosinovú větu přímo používá kalkulačka SUS trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- aritmetika
- odmocnina
- planimetrie
- Pythagorova věta
- mnohoúhelník
- trojúhelník
- kosočtverec
- úhlopříčka
- kosinová věta
- goniometrie a trigonometrie
- kosinus
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Trojuhelníku 135
 Trojuhelníku ABC o stranách a = 15 cm, b = 17,4 cm, c = 21,6 cm je opsána kružnice. Vypočítejte obsah úsečí určených stranami trojúhelníku.
Trojuhelníku ABC o stranách a = 15 cm, b = 17,4 cm, c = 21,6 cm je opsána kružnice. Vypočítejte obsah úsečí určených stranami trojúhelníku. - Pozorovatel 11
 Pozorovatel vidí letadlo pod výškovým úhlem 35° (úhel od vodorovné roviny). V tu chvíli letadlo hlásí výšku 4 km. Jak daleko od pozorovatele je místo, nad kterým letadlo letí. Zaokrouhli na stovky metrů.
Pozorovatel vidí letadlo pod výškovým úhlem 35° (úhel od vodorovné roviny). V tu chvíli letadlo hlásí výšku 4 km. Jak daleko od pozorovatele je místo, nad kterým letadlo letí. Zaokrouhli na stovky metrů. - Vzdálenost 145
 Vzdálenost tětivy od středu je 6 cm. Středový úhel je 60°. Vypočítejte plošný obsah kruhové úseče.
Vzdálenost tětivy od středu je 6 cm. Středový úhel je 60°. Vypočítejte plošný obsah kruhové úseče. - Kruh - úseč
 Kruh o průměru 30 cm je přeťat tětivou t = 16 cm. Vypočtěte obvod a obsah menší úseče.
Kruh o průměru 30 cm je přeťat tětivou t = 16 cm. Vypočtěte obvod a obsah menší úseče.
- Těžítko 3
 Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³?
Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³? - Trojúhelníku 83261
 Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3
Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3 - Rovnoramenném 83247
 Vypočítejte délky stran v rovnoramenném trojúhelníku, je-li dána výška (na základnu) Vc= 8,8cm a úhel u základny alfa= 38°40`.
Vypočítejte délky stran v rovnoramenném trojúhelníku, je-li dána výška (na základnu) Vc= 8,8cm a úhel u základny alfa= 38°40`. - V trojúhelníku 9
 V trojúhelníku ABC je velikost vnitřního úhlu beta dvojnásobkem velikosti úhlu alfa a velikosti úhlu gama je o 20 stupňů menší než velikost úhlu beta. Urči velikost všech vnitřních úhlů tohoto trojúhelníku.
V trojúhelníku ABC je velikost vnitřního úhlu beta dvojnásobkem velikosti úhlu alfa a velikosti úhlu gama je o 20 stupňů menší než velikost úhlu beta. Urči velikost všech vnitřních úhlů tohoto trojúhelníku. - Obrazec
 Obrazec se skládá z tmavého čtverce, dvou shodných bílých rovnoramenných trojúhelníků a dvou shodných bílých lichoběžníků. (S každou stranou čtverce splývá základna jednoho bílého útvaru. ) Tmavý čtverec má stranu délky 12 cm a jeho obsah je polovinou obs
Obrazec se skládá z tmavého čtverce, dvou shodných bílých rovnoramenných trojúhelníků a dvou shodných bílých lichoběžníků. (S každou stranou čtverce splývá základna jednoho bílého útvaru. ) Tmavý čtverec má stranu délky 12 cm a jeho obsah je polovinou obs
- Užitím 2
 Užitím kosinové věty dokažte, že v rovnoramenném trojúhelníku ABC se základnou AB platí, že c=2a cos α.
Užitím kosinové věty dokažte, že v rovnoramenném trojúhelníku ABC se základnou AB platí, že c=2a cos α. - V trojúhelníku 8
 V trojúhelníku ABC znáte poměr délek stran a:b:c=3:4:6. Vypočítejte velikosti úhlů trojúhelníku ABC.
V trojúhelníku ABC znáte poměr délek stran a:b:c=3:4:6. Vypočítejte velikosti úhlů trojúhelníku ABC. - Zatáčka 3
 Zatáčka má poloměr r = 100 m a je sklopena pod úhlem 20° vůči vodorovné rovině (= úhel klopení). Jaká je bezpečná (ta "nejlepší")rychlost při průjezdu touto zatáčkou? Načrtni obrázek z hlediska NIVS, vyznač síly a vypočítej.
Zatáčka má poloměr r = 100 m a je sklopena pod úhlem 20° vůči vodorovné rovině (= úhel klopení). Jaká je bezpečná (ta "nejlepší")rychlost při průjezdu touto zatáčkou? Načrtni obrázek z hlediska NIVS, vyznač síly a vypočítej. - Vzducholoď
 Vzducholoď je ve výšce x nad zemí. Pavel ji sleduje z místa A pod výškovým úhlem 18 stupnu 26 minut. V tutéž chvíli ji vidí Petr z malého letadla, které zrovna prolétá nad Pavlem ve výšce 150m. Petr vidí vzducholoď pod výškovým úhlem 11 stupnu a 46 minut.
Vzducholoď je ve výšce x nad zemí. Pavel ji sleduje z místa A pod výškovým úhlem 18 stupnu 26 minut. V tutéž chvíli ji vidí Petr z malého letadla, které zrovna prolétá nad Pavlem ve výšce 150m. Petr vidí vzducholoď pod výškovým úhlem 11 stupnu a 46 minut. - Z rozhledně
 Z rozhledně vysoké 40 m je vidět vrchol topolu pod hloubkovym uhlem o velikosti 50*10´a patu topolu v hloubkovem úhlu o velikosti 58*. Vypocitejte výšku topolu.
Z rozhledně vysoké 40 m je vidět vrchol topolu pod hloubkovym uhlem o velikosti 50*10´a patu topolu v hloubkovem úhlu o velikosti 58*. Vypocitejte výšku topolu.
- Dopravní 2
 Dopravní letadlo, které právě prolétá nad místem 2 400 m vzdáleném od místa pozorovatele, je vidět pod výškovým úhlem o velikosti 26° 20´. V jaké výšce letadlo letí?
Dopravní letadlo, které právě prolétá nad místem 2 400 m vzdáleném od místa pozorovatele, je vidět pod výškovým úhlem o velikosti 26° 20´. V jaké výšce letadlo letí? - Vypočítejte 82693
 Vypočítejte výšku stožáru, jehož patu vidíme v hloubkovém úhlu 11° a vrchol ve výškovém úhlu 28°. Stožár je pozorován z místa 10 m nad úrovní paty stožáru.
Vypočítejte výšku stožáru, jehož patu vidíme v hloubkovém úhlu 11° a vrchol ve výškovém úhlu 28°. Stožár je pozorován z místa 10 m nad úrovní paty stožáru. - Rovnoběžníku 82626
 Vypočítejte obsah rovnoběžníku, pokud známe obvod je 23 cm, úhlopříčka je 8,5 cm a jedna strana je o 1,5 cm delší.
Vypočítejte obsah rovnoběžníku, pokud známe obvod je 23 cm, úhlopříčka je 8,5 cm a jedna strana je o 1,5 cm delší.
