Pravouhlý
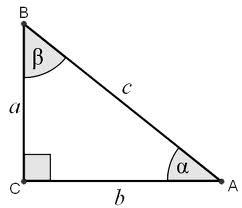
Určitě úhly pravoúhlého trojúhelníku, s přeponou c a odvesnamy a, b; jestliže platí:
2a+5b=5,064c
2a+5b=5,064c
Správná odpověď:
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- algebra
- kvadratická rovnice
- planimetrie
- Pythagorova věta
- pravoúhlý trojúhelník
- trojúhelník
- základní funkce
- úvaha
- goniometrie a trigonometrie
- sinus
- kosinus
- tangens
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Pozorovatelně 71934
 Letadlo letící směrem k pozorovatelně, z ní bylo zaměřeno v přímé vzdálenosti 5300 m pod výškovým úhlem 28º a po 9 sekundách v přímé vzdálenosti 2400 m pod výškovým úhlem 50º. Vypočítejte vzdálenost, kterou v tomto časovém intervalu letadlo prolétlo, jeho
Letadlo letící směrem k pozorovatelně, z ní bylo zaměřeno v přímé vzdálenosti 5300 m pod výškovým úhlem 28º a po 9 sekundách v přímé vzdálenosti 2400 m pod výškovým úhlem 50º. Vypočítejte vzdálenost, kterou v tomto časovém intervalu letadlo prolétlo, jeho - Knihovně 64324
 V městské knihovně vzrostl v roce 2008 počet knih o 0,2% a v roce 2009 vzrostl počet knih o 0,6%. Přitom celkový počet knih zůstal menší než 300 000. Kolik knih přibylo v městské knihovně v roce 2009?
V městské knihovně vzrostl v roce 2008 počet knih o 0,2% a v roce 2009 vzrostl počet knih o 0,6%. Přitom celkový počet knih zůstal menší než 300 000. Kolik knih přibylo v městské knihovně v roce 2009? - Soukolí
 Hnané kolo o poloměru 2 je spojeno s hnacím kolem o poloměru 1 řemenicí o délce 17. Jaká je vzdálenost os kol?
Hnané kolo o poloměru 2 je spojeno s hnacím kolem o poloměru 1 řemenicí o délce 17. Jaká je vzdálenost os kol? - 3úhelník 35881
 Součet délek dvou stran b+c=12 cm Úhel beta=68 Úhel gama=42 narysuj 3úhelník ABC
Součet délek dvou stran b+c=12 cm Úhel beta=68 Úhel gama=42 narysuj 3úhelník ABC
- Dvanásťuholník
 Vypočítejte velikost menšího z úhlů, který určují přímky A1 A4 a A2 A10 v pravidelném dvanásťuholníku A1A2A3. .. A12. Výsledek uveďte v stupních.
Vypočítejte velikost menšího z úhlů, který určují přímky A1 A4 a A2 A10 v pravidelném dvanásťuholníku A1A2A3. .. A12. Výsledek uveďte v stupních. - Vypočtěte 5
 Vypočtěte velikosti vnitřních úhlů trojúhelníku, víte-li že tyto jsou v poměru 2 : 3 : 5
Vypočtěte velikosti vnitřních úhlů trojúhelníku, víte-li že tyto jsou v poměru 2 : 3 : 5 - Soustředné kružnice
 Dvě soustředné kružnice s poloměry 1 a 9 ohraničují mezikruží. Tomuto mezikruží je vepsaných n kruhů, které se nepřekrývají. Stanovte nejvyšší možnou hodnotu n.
Dvě soustředné kružnice s poloměry 1 a 9 ohraničují mezikruží. Tomuto mezikruží je vepsaných n kruhů, které se nepřekrývají. Stanovte nejvyšší možnou hodnotu n. - Ručičky hodin
 Jakou velikost má tupý úhel, který svírají ručičky hodin o 12:20?
Jakou velikost má tupý úhel, který svírají ručičky hodin o 12:20? - Dron
 Létající dron zaměřoval území pro architekta. Vzlétl kolmo z bodu C do bodu D. Byl ve výšce 300 m nad rovinou ABC. Dron z bodu D zaměřil úhel BDC 43°. Vypočítejte v metrech vzdálenost bodů C a B.
Létající dron zaměřoval území pro architekta. Vzlétl kolmo z bodu C do bodu D. Byl ve výšce 300 m nad rovinou ABC. Dron z bodu D zaměřil úhel BDC 43°. Vypočítejte v metrech vzdálenost bodů C a B.
- Pětiúhelník 3
 Pruh papíru ve tvaru obdélníka o rozměrech 16 x 4 cm je přeložen po délce tak, že pravý spodní roh je přiložen na levý horní roh. Jakou plochu má vzniklý pětiúhelník?
Pruh papíru ve tvaru obdélníka o rozměrech 16 x 4 cm je přeložen po délce tak, že pravý spodní roh je přiložen na levý horní roh. Jakou plochu má vzniklý pětiúhelník? - Výška trojúhelníku
 Vrcholy rovnostranného trojúhelníku leží na 3 různých rovnoběžkách. Prostřední je od krajních vzdálena 5 m, resp. 3 m. Vypočítejte výšku tohoto trojúhelníku.
Vrcholy rovnostranného trojúhelníku leží na 3 různých rovnoběžkách. Prostřední je od krajních vzdálena 5 m, resp. 3 m. Vypočítejte výšku tohoto trojúhelníku. - Kruhová železnice
 Železnice má propojit kruhovým obloukem místa A, B a C, jejichž vzdálenosti jsou |AB| = 30 km, |AC| = 95 km, |BC| = 70 km. Jakou délku bude mít trať z A do C?
Železnice má propojit kruhovým obloukem místa A, B a C, jejichž vzdálenosti jsou |AB| = 30 km, |AC| = 95 km, |BC| = 70 km. Jakou délku bude mít trať z A do C? - Vzdialenosti 11711
 Pozorovateľ sedí v miestnosti 2 m od okna širokého 50 cm. Rovnobežne vo vzdialenosti 500 m vedie cesta. Akou veľkou priemernou rýchlosťou ide cyklista po tejto ceste, keď ho pozorovateľ vidí 15 s?
Pozorovateľ sedí v miestnosti 2 m od okna širokého 50 cm. Rovnobežne vo vzdialenosti 500 m vedie cesta. Akou veľkou priemernou rýchlosťou ide cyklista po tejto ceste, keď ho pozorovateľ vidí 15 s? - Sestrojte 5
 Sestrojte kosočtverec ABCD tak, aby jeho úhlopříčka BD měla velikost 8 cm a vzdálenost vrcholu B od primky AD byla 5 cm. Určete všechny možnosti
Sestrojte kosočtverec ABCD tak, aby jeho úhlopříčka BD měla velikost 8 cm a vzdálenost vrcholu B od primky AD byla 5 cm. Určete všechny možnosti
- Na vrcholu
 Na vrcholu hory stojí hrad, který má věž vysokou 30m. Křižovatku cest v údolí vidíme z vrcholu věže a od její paty v hloubkových úhlech 32° 50 'a 30° 10'. Jak vysoko je vrchol hory nad křižovatkou?
Na vrcholu hory stojí hrad, který má věž vysokou 30m. Křižovatku cest v údolí vidíme z vrcholu věže a od její paty v hloubkových úhlech 32° 50 'a 30° 10'. Jak vysoko je vrchol hory nad křižovatkou? - Urči poloměr
 Urči poloměr podstavy kužele, jestliže jeho plášť se rozvine v kruhovou výseč s poloměrem „s"=10 a středovým úhlem x=60°. r=?, o=?
Urči poloměr podstavy kužele, jestliže jeho plášť se rozvine v kruhovou výseč s poloměrem „s"=10 a středovým úhlem x=60°. r=?, o=? - Rovnostranný 7962
 Po dlouhém večeři uvnitř salonku ve tvaru čtverce ABCD leží opilý kupec E tak, že trojúhelník DEC je rovnostranný. Na hraně BC leží špeh F, přičemž |EB|=|EF|. Jaká je velikost úhlu CEF?
Po dlouhém večeři uvnitř salonku ve tvaru čtverce ABCD leží opilý kupec E tak, že trojúhelník DEC je rovnostranný. Na hraně BC leží špeh F, přičemž |EB|=|EF|. Jaká je velikost úhlu CEF?
