Záhrada
Rozloha čtvercové zahrady tvoří 1/3 rozlohy zahrady tvaru trojúhelníku se stranami 120 m 75 m a 75 m.
Kolik metrů pletiva potřebuji na oplocení čtvercové zahrady?
Kolik metrů pletiva potřebuji na oplocení čtvercové zahrady?
Správná odpověď:

Tipy na související online kalkulačky
Vyzkoušejte naši kalkulačka na přepočet poměru.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Chcete proměnit jednotku délky?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Chcete proměnit jednotku délky?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- algebra
- rovnice
- aritmetika
- odmocnina
- druhá mocnina
- planimetrie
- Pythagorova věta
- pravoúhlý trojúhelník
- obsah
- obvod
- trojúhelník
- čtverec
- základní funkce
- úměra, poměr
- úvaha
- čísla
- reálná čísla
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Koberec 9
 Kolik metrů koberce širokého 3 metry je třeba na pokrytí čtvercové podlahy s obsahem 36m čtverečních?
Kolik metrů koberce širokého 3 metry je třeba na pokrytí čtvercové podlahy s obsahem 36m čtverečních? - Pletivo
 Kolik metrů pletiva je třeba na oplocení čtvercové zahrady o výměře 5 402,25m čtverečních.
Kolik metrů pletiva je třeba na oplocení čtvercové zahrady o výměře 5 402,25m čtverečních. - Vypočítej 83251
 Vypočítej obvod čtverce, jehož obsah je 25 dm² .
Vypočítej obvod čtverce, jehož obsah je 25 dm² . - Pilíř 3
 Kolik betonu je třeba na vylití 8 betonových sloupů s podstavou čtverce: a = 38cm, výška sloupů je 6,2m? V každém sloupu je dutina válce o průměru 15cm.
Kolik betonu je třeba na vylití 8 betonových sloupů s podstavou čtverce: a = 38cm, výška sloupů je 6,2m? V každém sloupu je dutina válce o průměru 15cm.
- Obrazec
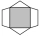 Obrazec se skládá z tmavého čtverce, dvou shodných bílých rovnoramenných trojúhelníků a dvou shodných bílých lichoběžníků. (S každou stranou čtverce splývá základna jednoho bílého útvaru. ) Tmavý čtverec má stranu délky 12 cm a jeho obsah je polovinou obs
Obrazec se skládá z tmavého čtverce, dvou shodných bílých rovnoramenných trojúhelníků a dvou shodných bílých lichoběžníků. (S každou stranou čtverce splývá základna jednoho bílého útvaru. ) Tmavý čtverec má stranu délky 12 cm a jeho obsah je polovinou obs - Pravoúhlý 37
 Pravoúhlý trojúhelník má obsah 36 cm². V něm je umístěn čtverec tak, že dvě strany čtverce jsou částmi dvou stran trojúhelníku a jeden vrchol čtverce je ve třetině nejdelší strany. Určete obsah tohoto čtverce.
Pravoúhlý trojúhelník má obsah 36 cm². V něm je umístěn čtverec tak, že dvě strany čtverce jsou částmi dvou stran trojúhelníku a jeden vrchol čtverce je ve třetině nejdelší strany. Určete obsah tohoto čtverce. - Čtverec 109
 Čtverec na obrázku má délku strany 6cm. Kolik procent z obsahu tvoří vybarvená část?
Čtverec na obrázku má délku strany 6cm. Kolik procent z obsahu tvoří vybarvená část? - Obdélníkovými 82582
 Obdélníkovými dlaždicemi se stranami 168cm a 280cm máme vydláždit co nejmenší čtverec. Jaká bude jeho strana čtverce?
Obdélníkovými dlaždicemi se stranami 168cm a 280cm máme vydláždit co nejmenší čtverec. Jaká bude jeho strana čtverce? - Pšenice
 Z 37 hektarů pšenice sklidili zemědělci 1110q obilí. a) kolik q pšenice sklidili z 12 hektarů. b) kolik zrní se sklidilo z 1 m². C) jak velká strana čtverce pole, z kterého sklidili 1q pšenice?
Z 37 hektarů pšenice sklidili zemědělci 1110q obilí. a) kolik q pšenice sklidili z 12 hektarů. b) kolik zrní se sklidilo z 1 m². C) jak velká strana čtverce pole, z kterého sklidili 1q pšenice?
- Kolik 143
 Kolik metrů pletiva je třeba k oplocení čtvercového pozemku, jehož strana měří 20m?
Kolik metrů pletiva je třeba k oplocení čtvercového pozemku, jehož strana měří 20m? - Dokonalý čtverec
 Klasifikovali byste 324 jako dokonalý čtverec, dokonalou kostku, obojí nebo ani jedno? ...
Klasifikovali byste 324 jako dokonalý čtverec, dokonalou kostku, obojí nebo ani jedno? ... - Vypočítejte 248
 Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66°
Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66° - Vypočítej 391
 Vypočítej objem pravidelného čtyřbokého jehlanu s podstavou čtverce o straně a = 3 cm a délkou boční hrany b = 7 cm
Vypočítej objem pravidelného čtyřbokého jehlanu s podstavou čtverce o straně a = 3 cm a délkou boční hrany b = 7 cm - Stranu
 Stranu čtverce jsme z původních 15cm zvětšili o 12%. Za a, jaký byl obvod a obsah nového čtverce. za b, o kolik procent se zvětšil obvod a obsah.
Stranu čtverce jsme z původních 15cm zvětšili o 12%. Za a, jaký byl obvod a obsah nového čtverce. za b, o kolik procent se zvětšil obvod a obsah.
- Ortocentrum
 Je dán trojúhelník ABC: A (-1,3), B(2,-2), C(-4,-3). Urči souřadnice průsečíku výšek a souřadnice průsečík os stran.
Je dán trojúhelník ABC: A (-1,3), B(2,-2), C(-4,-3). Urči souřadnice průsečíku výšek a souřadnice průsečík os stran. - Srážkoměr
 Srážkoměr ukázal že na čtvercovou zahradu pana severy napršela osmimilimetrová vrstva vody kdyby chtěl pan Severa docílit stejnou závlahu zahrady musel by použít 200 plných šestnáctilitrových konví. vypočítejte výměru jeho zahrady.
Srážkoměr ukázal že na čtvercovou zahradu pana severy napršela osmimilimetrová vrstva vody kdyby chtěl pan Severa docílit stejnou závlahu zahrady musel by použít 200 plných šestnáctilitrových konví. vypočítejte výměru jeho zahrady. - Poloměr 12
 Poloměr kruhového záhonu je 2 m. Okolo něho je plocha vysypaná pískem, jejíž hranici tvoří strany čtverce o délce 5 m a obvod záhonu. Vypočítejte obsah plochy vysypané pískem.
Poloměr kruhového záhonu je 2 m. Okolo něho je plocha vysypaná pískem, jejíž hranici tvoří strany čtverce o délce 5 m a obvod záhonu. Vypočítejte obsah plochy vysypané pískem.
