Biliardové gule
Vrstva slonovinových biliardových gúľ o polomere 6,35 cm, je v tvare štvorca. Gule sú usporiadané tak, že každá guľa je tangenta (dotýka sa) každej susediacej s ňou. V priestoroch medzi 4 priľahlými guľami je priestor rovný veľkosti originálej guli. Po sebe idúce vrstvy vytvárajú pyramídu s jednou guľou na vrchole. V prípade, že spodná vrstva obsahuje 16 lôpt, aká je výška hromady?
Správna odpoveď:

Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Guľová vrstva
 Aký je objem guľovej vrstvy, ktorá zostane po odrezaní odsekov z oboch strán gule, ktorých výška je 3,5 cm, Priemer gule je 24 cm.
Aký je objem guľovej vrstvy, ktorá zostane po odrezaní odsekov z oboch strán gule, ktorých výška je 3,5 cm, Priemer gule je 24 cm. - Delové guľe
 Z troch delových gúľ s priemerom 16 cm, ktoré pri bitke dopadli na hradné nádvorie, ulial hradný kováč gule s priemerom 10 cm, ktoré sa hodili do diel umiestnených na hradbách. Koľko ulial kováč gulí?
Z troch delových gúľ s priemerom 16 cm, ktoré pri bitke dopadli na hradné nádvorie, ulial hradný kováč gule s priemerom 10 cm, ktoré sa hodili do diel umiestnených na hradbách. Koľko ulial kováč gulí? - Gule v guľi
 Koľko gúľ s polomerom 15 cm sa vojde do väčšej gule s polomerom 150 cm?
Koľko gúľ s polomerom 15 cm sa vojde do väčšej gule s polomerom 150 cm? - Polgula odsek, vrchlík
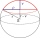 Vypočítajte objem guľovej vrstvy, ktorá zostane z polgule po odrezaní odseku s výškou 3 cm. Výška polgule je 10 cm.
Vypočítajte objem guľovej vrstvy, ktorá zostane z polgule po odrezaní odseku s výškou 3 cm. Výška polgule je 10 cm.
- Rúry
 Železné rúry v sklade sa ukladajú do vrstiev tak, že rúry každej vrchnej vrstvy zapadajú do medzier spodnej vrstvy. Do koľkých vrstiev sa uloží 81 rúr, ak najvrchnejšia vrstva má 5 rúr? Koľko rúr má najspodnejšia vrstva?
Železné rúry v sklade sa ukladajú do vrstiev tak, že rúry každej vrchnej vrstvy zapadajú do medzier spodnej vrstvy. Do koľkých vrstiev sa uloží 81 rúr, ak najvrchnejšia vrstva má 5 rúr? Koľko rúr má najspodnejšia vrstva? - Rovnoramenné váhy
 Predstav si, že máš 9 vzhľadovo úplne rovnakých gúľ z ktorých 1 má väčšiu hmotnosť ako ostatné k dispozícii máš rovnoramenné váhy. Napíš postup ako by si pomocou váženia zistil, ktorá je ťažšia gule. Koľko najmenej meraní musíš urobiť?
Predstav si, že máš 9 vzhľadovo úplne rovnakých gúľ z ktorých 1 má väčšiu hmotnosť ako ostatné k dispozícii máš rovnoramenné váhy. Napíš postup ako by si pomocou váženia zistil, ktorá je ťažšia gule. Koľko najmenej meraní musíš urobiť? - Vo vnútri
 Vo vnútri kocky s hranou 10 cm je umiestnená guľa tak, že sa dotýka všetkých stien kocky. Koľko percent objemu kocky tvorí objem gule?
Vo vnútri kocky s hranou 10 cm je umiestnená guľa tak, že sa dotýka všetkých stien kocky. Koľko percent objemu kocky tvorí objem gule? - Gule v urne
 V urne je 8 bielych a 6 čiernych gulí. Náhodne vytiahneme 4 gule. Aká je pravdepodobnosť, že medzi nimi budú 2 biele?
V urne je 8 bielych a 6 čiernych gulí. Náhodne vytiahneme 4 gule. Aká je pravdepodobnosť, že medzi nimi budú 2 biele? - Určte 10
 Určte objem guľovej vrstvy, ktorá vznikne z polgule s polomerom 5 cm odrezaním odseku, ktorého výška je 1,5 cm.
Určte objem guľovej vrstvy, ktorá vznikne z polgule s polomerom 5 cm odrezaním odseku, ktorého výška je 1,5 cm.
- Stožiar
 Stožiar vysoký 32 metrov bol vetrom zlomený tak, že sa jeho vrchol dotýka zeme 16 metrov od päty stožiaru. Ešte stojaca časť stožiaru, zlomená časť a zeme vytvárajú pravouhlý trojuholník. V akej výške bol stožiar zlomený?
Stožiar vysoký 32 metrov bol vetrom zlomený tak, že sa jeho vrchol dotýka zeme 16 metrov od päty stožiaru. Ešte stojaca časť stožiaru, zlomená časť a zeme vytvárajú pravouhlý trojuholník. V akej výške bol stožiar zlomený? - Cukrárskej 7318
 Cukrárka potrebuje z cukrárskej hmoty v tvare gule o polomere 25cm vyrezať ozdobu v tvare kužeľa. Určte polomer podstavy ozdoby a (a výšku h) tak, aby sa na výrobu ozdoby použilo čo najviac hmoty.
Cukrárka potrebuje z cukrárskej hmoty v tvare gule o polomere 25cm vyrezať ozdobu v tvare kužeľa. Určte polomer podstavy ozdoby a (a výšku h) tak, aby sa na výrobu ozdoby použilo čo najviac hmoty. - Prevŕtaním 70684
 Zlatý prstienok o šírke 1 cm je vyrobený prevŕtaním gule o polomere 1 cm cez jej stred. Zlatý náramok o šírke 1 cm je vyrobený prevŕtaním gule o polomere 4 cm cez jej stred. Ktorý šperk bude mať väčšiu cenu, ak budeme brať do úvahy iba množstvo drahého ko
Zlatý prstienok o šírke 1 cm je vyrobený prevŕtaním gule o polomere 1 cm cez jej stred. Zlatý náramok o šírke 1 cm je vyrobený prevŕtaním gule o polomere 4 cm cez jej stred. Ktorý šperk bude mať väčšiu cenu, ak budeme brať do úvahy iba množstvo drahého ko - Aká je 16
 Aká je pravdepodobnosť, že pri hode mincou 5x po sebe padne hlava? Výsledok zapíšte v tvare zlomku.
Aká je pravdepodobnosť, že pri hode mincou 5x po sebe padne hlava? Výsledok zapíšte v tvare zlomku. - Ukážte,
 Ukážte, že ak x, y, z sú 3 po sebe idúce nenulové cifry, tak zyx-xyz=198, kde zyx a xyz sú trojciferné čísla vytvorené z cifier x, y, z.
Ukážte, že ak x, y, z sú 3 po sebe idúce nenulové cifry, tak zyx-xyz=198, kde zyx a xyz sú trojciferné čísla vytvorené z cifier x, y, z.
- Mimozemská loď
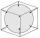 Mimozemská loď má tvar gule o polomere r = 3000m a jej posádka potrebuje loďou odviezť nazbieraný výskumný materiál v boxe v tvare kvádra so štvorcovou podstavou. Určte dĺžku podstavy a (a výšku h) tak, aby mal box najväčší možný objem.
Mimozemská loď má tvar gule o polomere r = 3000m a jej posádka potrebuje loďou odviezť nazbieraný výskumný materiál v boxe v tvare kvádra so štvorcovou podstavou. Určte dĺžku podstavy a (a výšku h) tak, aby mal box najväčší možný objem. - Šperk
 V súťaži o najkrajší šperk vyhral šperk s nasledovným popisom: na striebornej doštičke v tvare štvorca sú osadené štyri zhodné rubínové kosoštvorce. Kosoštvorce sa vrcholmi dotýkajú v stredoch strán štvorca, dĺžka každej z nich je šestinou uhlopriečky štv
V súťaži o najkrajší šperk vyhral šperk s nasledovným popisom: na striebornej doštičke v tvare štvorca sú osadené štyri zhodné rubínové kosoštvorce. Kosoštvorce sa vrcholmi dotýkajú v stredoch strán štvorca, dĺžka každej z nich je šestinou uhlopriečky štv - Preusporiadaním 81898
 Uvažujeme „slová“ (tj ľubovoľné reťazce písmen) obdržané preusporiadaním písmen slova „AKVARISTIKA“. Všetky písmená sú tu vzájomne rozlíšiteľné. Počet takých slov, ktoré zároveň obsahujú výraz „KAVA“ (ako po sebe idúce písmená v danom poradí), je rovný: (
Uvažujeme „slová“ (tj ľubovoľné reťazce písmen) obdržané preusporiadaním písmen slova „AKVARISTIKA“. Všetky písmená sú tu vzájomne rozlíšiteľné. Počet takých slov, ktoré zároveň obsahujú výraz „KAVA“ (ako po sebe idúce písmená v danom poradí), je rovný: (
