Marienka - mo
Marienka rozmiestni do vrcholov pravidelného osemuholníka rôzne počty od jedného po osem cukríkov. Peter si potom môže vybrať, ktoré tri kôpky cukríkov dá Marienke, ostatné si ponechá. Jedinou podmienkou je, že tieto tri kôpky ležia vo vrcholoch rovnoramenného trojuholníka. Marienka chce rozmiestniť cukríky tak, aby ich dostala čo najviac, nech už Peter trojicu vrcholov vyberie akokoľvek. Koľko ich tak Marienka zaručene získa?
b) Rovnakú úlohu vyriešte aj pre pravidelný deväťuholník, do ktorého vrcholov rozmiestni Marienka 1 až 9 cukríkov. (Medzi rovnoramenné trojuholníky zaraďujeme aj trojuholníky rovnostranné.)
b) Rovnakú úlohu vyriešte aj pre pravidelný deväťuholník, do ktorého vrcholov rozmiestni Marienka 1 až 9 cukríkov. (Medzi rovnoramenné trojuholníky zaraďujeme aj trojuholníky rovnostranné.)
Správna odpoveď:

Zobrazujem 4 komentáre:
Www
treba si to nakreslit; a cukriky davat tak aby na vrcholoch rovnostrannych trojuholnikov v sucte bolo vzdy najnizsie mozne cislo. Cize jeden taky trojuholnik bude mat na vrcholoch cisla 1+8+3=12, dalsi 2+7+4=13 atd. Cize sucet 12,13 max 15 vyberie Peter. Cize Marienka ziska 1+2+3+4+5+6+7+8 -8-7
Žiak
no ja si myslim ze marienka moze zistak od 6(1+2+3) az po 21(6+7+8) ale riesenie bude cize marienka ZARUCENE ziska 6 ale ked ich mudro rozmiestni tak ich moze ziskat az 10 mozno aj 11
9uholnik som este neriesil.
9uholnik som este neriesil.
Www
ked bude marienka davat cisla zle, tak moze byt vysledok 6. Ale to odporuje zadaniu - "Marienka chce rozmiestniť cukríky tak, aby ich dostala čo najviac". Cize neumiestni tri najmensie cisla na vrcholy jedneho trojuholnika, ale cisla na stranach rovnomerne rozmiestni, aby sucet na lubovolnom trojuholniku bol priblizne 12 az 15...
Tipy na súvisiace online kalkulačky
Vypočet rovnoramenného trojuholníka.
Vypočet rovnostranného trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vypočet rovnostranného trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Jednotky fyzikálnych veličín:
Téma:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Katka MO
 Katka narysovala trojuholník ABC. Stred strany AB si označila ako X a stred strany AC ako Y. Na strane BC chce nájsť taký bod Z, aby obsah štvoruholníka AXZY bol čo najväčší. Akú časť trojuholníka ABC môže maximálne zaberať štvoruholník AXZY?
Katka narysovala trojuholník ABC. Stred strany AB si označila ako X a stred strany AC ako Y. Na strane BC chce nájsť taký bod Z, aby obsah štvoruholníka AXZY bol čo najväčší. Akú časť trojuholníka ABC môže maximálne zaberať štvoruholník AXZY? - V košíku 5
 V košíku je 12 jabĺk a 10 hrušiek. Peter si má z nich vybrať buď jablko alebo hrušku tak, aby Viera, ktorá si po ňom vyberie 1 jablko a 1 hrušku, mala čo najväčšiu možnosť výberu. Určte, čo si Peter vyberie.
V košíku je 12 jabĺk a 10 hrušiek. Peter si má z nich vybrať buď jablko alebo hrušku tak, aby Viera, ktorá si po ňom vyberie 1 jablko a 1 hrušku, mala čo najväčšiu možnosť výberu. Určte, čo si Peter vyberie. - ROZDEĽ CUKRIKY
 Mamka kúpila svojim deťom balík cukríkov.Všetkých 116 cukríkov z balíka rozdelila medzi svojich 3 detí tak, aby každé dieťa dostalo čo najviac a aby jej zostalo čo najmenej cukríkov. Koľko cukríkov zostalo mamke?
Mamka kúpila svojim deťom balík cukríkov.Všetkých 116 cukríkov z balíka rozdelila medzi svojich 3 detí tak, aby každé dieťa dostalo čo najviac a aby jej zostalo čo najmenej cukríkov. Koľko cukríkov zostalo mamke? - Predpokladajme 62424
 Deryl si chce ušetriť peniaze, aby sa zabezpečil na dôchodok. Po uplynutí jedného roka začne každý rok ukladať rovnakú pevnú sumu počas nasledujúcich 30 rokov na dôchodkový sporiaci účet. Po uplynutí jedného roka od vykonania posledného vkladu vyberie 100
Deryl si chce ušetriť peniaze, aby sa zabezpečil na dôchodok. Po uplynutí jedného roka začne každý rok ukladať rovnakú pevnú sumu počas nasledujúcich 30 rokov na dôchodkový sporiaci účet. Po uplynutí jedného roka od vykonania posledného vkladu vyberie 100
- Zo štvorca 2
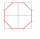 Zo štvorca o strane 4 cm odrežeme štyri pravouhlé rovnoramenné trojuholníky s pravým uhlom vo vrcholoch štvorca a s preponou √2 cm. Dostaneme osemuholník. Vypočítajte jeho obvod, ak plocha osemuholníka je 14cm².
Zo štvorca o strane 4 cm odrežeme štyri pravouhlé rovnoramenné trojuholníky s pravým uhlom vo vrcholoch štvorca a s preponou √2 cm. Dostaneme osemuholník. Vypočítajte jeho obvod, ak plocha osemuholníka je 14cm². - Jana
 Jana, Martina a Zuzka si rozdelili cukríky v pomere 3:7:5. Martina dostala o 9 cukríkov menej ako mali Jana a Zuzka spolu. Ktoré tvrdenie je pravdivé? A. Martina dostala menej cukríkov ako Zuzka. B. Všetky spolu dostali 135 cukríkov. C. Martina dostala o
Jana, Martina a Zuzka si rozdelili cukríky v pomere 3:7:5. Martina dostala o 9 cukríkov menej ako mali Jana a Zuzka spolu. Ktoré tvrdenie je pravdivé? A. Martina dostala menej cukríkov ako Zuzka. B. Všetky spolu dostali 135 cukríkov. C. Martina dostala o - V nepriehľadnom
 V nepriehľadnom balíčku je 5 citrónových, 6 jablkových a 3 jahodové cukríky. Najmenej koľko cukríkov musíme vybrať, aby bol medzi nimi aspoň jeden jahodový?
V nepriehľadnom balíčku je 5 citrónových, 6 jablkových a 3 jahodové cukríky. Najmenej koľko cukríkov musíme vybrať, aby bol medzi nimi aspoň jeden jahodový? - Dvojciferné číslo 2
 Adela si myslela dvojciferné číslo sčítala ho s jeho desaťnásobkom a dostala 407. Ktoré číslo si myslela?
Adela si myslela dvojciferné číslo sčítala ho s jeho desaťnásobkom a dostala 407. Ktoré číslo si myslela? - Rovnoramenné váhy
 Predstav si, že máš 9 vzhľadovo úplne rovnakých gúľ z ktorých 1 má väčšiu hmotnosť ako ostatné k dispozícii máš rovnoramenné váhy. Napíš postup ako by si pomocou váženia zistil, ktorá je ťažšia gule. Koľko najmenej meraní musíš urobiť?
Predstav si, že máš 9 vzhľadovo úplne rovnakých gúľ z ktorých 1 má väčšiu hmotnosť ako ostatné k dispozícii máš rovnoramenné váhy. Napíš postup ako by si pomocou váženia zistil, ktorá je ťažšia gule. Koľko najmenej meraní musíš urobiť?
- Pravdepodobnosť 81637
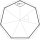 Z vrcholov pravidelného sedemuholníka vyberieme náhodne trojicu rôznych bodov a spojíme ich úsečkami. Pravdepodobnosť, že výsledný trojuholník bude rovnoramenný, je rovná: (A) 1/3 (B) 2/5 (C) 3/5 (D) 4/7
Z vrcholov pravidelného sedemuholníka vyberieme náhodne trojicu rôznych bodov a spojíme ich úsečkami. Pravdepodobnosť, že výsledný trojuholník bude rovnoramenný, je rovná: (A) 1/3 (B) 2/5 (C) 3/5 (D) 4/7 - Dve deti
 Rodina disponuje sumou 5000 €, ktoré chce rozdeliť medzi ich dve deti vo veku 10 a 14 rokov. Každému dieťaťu zriadia účet v tej istej banke úročený štvrťročne pevnou ročnou úrokovou sadzbou 2,75 %. Určte ako musí rodina rozdeliť disponibilnú sumu na tieto
Rodina disponuje sumou 5000 €, ktoré chce rozdeliť medzi ich dve deti vo veku 10 a 14 rokov. Každému dieťaťu zriadia účet v tej istej banke úročený štvrťročne pevnou ročnou úrokovou sadzbou 2,75 %. Určte ako musí rodina rozdeliť disponibilnú sumu na tieto - Pravdepodobnosť 69914
 Pri skúške dostane každý študent 30 rôznych otázok, z nich vyberie náhodne 3. Na úspešné zloženie skúšky je potrebné, aby dokázal dve správne zodpovedať. aká je pravdepodobnosť, že študent uspeje, ak zvládol 70% otázok (naučený je 70% otázok)?
Pri skúške dostane každý študent 30 rôznych otázok, z nich vyberie náhodne 3. Na úspešné zloženie skúšky je potrebné, aby dokázal dve správne zodpovedať. aká je pravdepodobnosť, že študent uspeje, ak zvládol 70% otázok (naučený je 70% otázok)? - Vypočítaj 393
 Vypočítaj, koľko volejbalových lôpt s obvodom 65 cm sa zmestí do stojana tvaru kocky, ktorého hrana má dĺžku 100 cm.
Vypočítaj, koľko volejbalových lôpt s obvodom 65 cm sa zmestí do stojana tvaru kocky, ktorého hrana má dĺžku 100 cm. - Chovprodukt
 Z chovproduktu (Zverimexu) vypredávali rybky z jedného akvária. Ondrej chcel polovicu všetkých rybiek, ale aby nemuseli žiadnu rybku rezať, dostal o polovicu rybky viac, ako požadoval. Matej si prial polovicu zvyšných rybiek, ale rovnako ako Ondrej dostal
Z chovproduktu (Zverimexu) vypredávali rybky z jedného akvária. Ondrej chcel polovicu všetkých rybiek, ale aby nemuseli žiadnu rybku rezať, dostal o polovicu rybky viac, ako požadoval. Matej si prial polovicu zvyšných rybiek, ale rovnako ako Ondrej dostal
- Tetraéder
 Určte polohu ťažiska sústavy štyroch hmotných bodov, ktoré majú hmotnosti, m1, m2=2m1, m3=3m1 a m4=4m1, ak ležia vo vrcholoch rovnorameného tetraédra. (vo všetkých pripadoch medzi susednými hmotnymi bodmi je vzd
Určte polohu ťažiska sústavy štyroch hmotných bodov, ktoré majú hmotnosti, m1, m2=2m1, m3=3m1 a m4=4m1, ak ležia vo vrcholoch rovnorameného tetraédra. (vo všetkých pripadoch medzi susednými hmotnymi bodmi je vzd - MO Z6-I-3 2022
 Magda si vystrihla dva rovnaké rovnoramenné trojuholníky, z ktorých každý mal obvod 100 cm. Najprv z týchto trojuholníkov zložila štvoruholník tak, že ich k sebe priložila ramenami. Potom z nich zložila štvoruholník tak, že ich k sebe priložila základňami
Magda si vystrihla dva rovnaké rovnoramenné trojuholníky, z ktorých každý mal obvod 100 cm. Najprv z týchto trojuholníkov zložila štvoruholník tak, že ich k sebe priložila ramenami. Potom z nich zložila štvoruholník tak, že ich k sebe priložila základňami - Bonboniéra
 V bonboniére bolo 16 cukríkov. Kryštof a Lukaš si ich rozdelil tak, že: a) Krištof mal o 4 cukríky viac ako Lukaš, b) Krištof mal o 6 bombona menej ako Lukaš, c) Krištof mal 3krát viac cukríkov ako Lukaš. Koľko mal každý z chlapcov cukríkov?
V bonboniére bolo 16 cukríkov. Kryštof a Lukaš si ich rozdelil tak, že: a) Krištof mal o 4 cukríky viac ako Lukaš, b) Krištof mal o 6 bombona menej ako Lukaš, c) Krištof mal 3krát viac cukríkov ako Lukaš. Koľko mal každý z chlapcov cukríkov?
