Vpísaná kružnica
Do pravouhlého trojuholníka XYZ s pravým uhlom pri vrchole X je vpísaná kružnica s polomerom 5 cm. Určte obsah trojuholníka XYZ ak XZ=14cm.
Správna odpoveď:
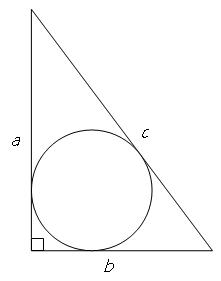
Zobrazujem 2 komentáre:
Yuri
Ak sa nemýlim jedná sa o nejakú úpravu herónovho vzorca... S=sr som nepochopil odkial máme... chcem sa spýtať bez použitia herónovho vzorca by sa to nedalo?? (použiť nejakú vlastnosť vpísanej kružnice...)
Ivo
Nas vynalez to neni; pozrite tiez:
https://cs.wikipedia.org/wiki/Kru%C5%BEnice_vepsan%C3%A1
https://sk.wikipedia.org/wiki/Trojuholn%C3%ADk#Kru.C5.BEnica_vp.C3.ADsan.C3.A1_trojuholn.C3.ADku
S = s*r
https://cs.wikipedia.org/wiki/Kru%C5%BEnice_vepsan%C3%A1
https://sk.wikipedia.org/wiki/Trojuholn%C3%ADk#Kru.C5.BEnica_vp.C3.ADsan.C3.A1_trojuholn.C3.ADku
S = s*r
Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Pravouhlý lichobežník
 Vypočítajte obsah pravouhlého lichobežníka ABCD s pravým uhlom pri vrchole A: a = 3 dm b = 5 dm c = 6 dm d = 4 dm
Vypočítajte obsah pravouhlého lichobežníka ABCD s pravým uhlom pri vrchole A: a = 3 dm b = 5 dm c = 6 dm d = 4 dm - Obsah 41
 Obsah pravouhlého trojuholníka KLM s pravým uhlom pri vrchole L je 60 mm štvorcových a jeho odvesna k má dĺžku 10 mm. Trojuholníky KLM a RST sú podobné, pomer podobnosti je k=2,5 . Vypočítaj obsah trojuholníka RST.
Obsah pravouhlého trojuholníka KLM s pravým uhlom pri vrchole L je 60 mm štvorcových a jeho odvesna k má dĺžku 10 mm. Trojuholníky KLM a RST sú podobné, pomer podobnosti je k=2,5 . Vypočítaj obsah trojuholníka RST. - Pravoúhly
 Pravoúhly lichobežník ABCD s pravým uhlom pri vrchole A má strany a, b, c, d . Vypočítaj obvod a obsah lichobežníka, ak je dané : a=25cm, c=10cm, d= 8cm
Pravoúhly lichobežník ABCD s pravým uhlom pri vrchole A má strany a, b, c, d . Vypočítaj obvod a obsah lichobežníka, ak je dané : a=25cm, c=10cm, d= 8cm - Euklid bez euklida
 Majme pravouhlý trojuholník ABC s pravým uhlom pri vrchole C, |BC|=19, |AB|=26. Vypočítejte výšku v trojuholníka bez použitia Euklidových viet.
Majme pravouhlý trojuholník ABC s pravým uhlom pri vrchole C, |BC|=19, |AB|=26. Vypočítejte výšku v trojuholníka bez použitia Euklidových viet.
- Euklid2
 V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C je daná odvesna a = 17 a výška v = 11. Určite obvod trojuholníka.
V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C je daná odvesna a = 17 a výška v = 11. Určite obvod trojuholníka. - Trojuholník ABC
 Majme pravouhlý trojuholník ABC s pravým uhlom pri vrchole C, |BC|=18, |AB|=33. Vypočítejte výšku vAB trojuholníka na stranu AB.
Majme pravouhlý trojuholník ABC s pravým uhlom pri vrchole C, |BC|=18, |AB|=33. Vypočítejte výšku vAB trojuholníka na stranu AB. - Trojuholník ABC
 V trojuholníku ABC so stranou BC dĺžky 2 cm je bod K stredom strany AB. Body L a M rozdeľujú stranu AC na tri zhodné úsečky. Trojuholník KLM je rovnoramenný s pravým uhlom pri vrchole K. Určte dĺžky strán AB, AC trojuholníka ABC.
V trojuholníku ABC so stranou BC dĺžky 2 cm je bod K stredom strany AB. Body L a M rozdeľujú stranu AC na tri zhodné úsečky. Trojuholník KLM je rovnoramenný s pravým uhlom pri vrchole K. Určte dĺžky strán AB, AC trojuholníka ABC. - Trojuholníku 6568
 V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C je dané : a=17cm, Vc=8 cm. Vypočítajte dĺžku strán b, c, jeho obsah S, obvod o, dĺžku polomerov kružníc trojuholníka opísané R a vpísané r a veľkosť uhlov alfa a beta.
V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C je dané : a=17cm, Vc=8 cm. Vypočítajte dĺžku strán b, c, jeho obsah S, obvod o, dĺžku polomerov kružníc trojuholníka opísané R a vpísané r a veľkosť uhlov alfa a beta. - Zistite 4
 Zistite, či trojuholník ABC (s pravým uhlom pri vrchole C) je pravouhlý, ak: a) a= 3dm, b=40cm, c=0,5m b) a= 8dm, b=1,2m, c=6dm
Zistite, či trojuholník ABC (s pravým uhlom pri vrchole C) je pravouhlý, ak: a) a= 3dm, b=40cm, c=0,5m b) a= 8dm, b=1,2m, c=6dm
- V pravouhlom 7
 V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C poznáme dĺžky strán AC = 9 cm a BC = 7 cm. Vypočítajte dĺžku poslednej strany trojuholníka a veľkosť všetkých uhlov.
V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C poznáme dĺžky strán AC = 9 cm a BC = 7 cm. Vypočítajte dĺžku poslednej strany trojuholníka a veľkosť všetkých uhlov. - V pravouhlom 8
 V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C poznáme dĺžku strany AB = 24 cm a uhol pri vrchole B = 71°. Vypočítajte dĺžku odvesien trojuholníka.
V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C poznáme dĺžku strany AB = 24 cm a uhol pri vrchole B = 71°. Vypočítajte dĺžku odvesien trojuholníka. - Uhlopriečka lichobežníka
 Určte dĺžku uhlopriečky BD v pravouhlom lichobežníka ABCD s pravým uhlom pri vrchole A, keď / AD / = 8,1 cm a uhol DBA je 42°
Určte dĺžku uhlopriečky BD v pravouhlom lichobežníka ABCD s pravým uhlom pri vrchole A, keď / AD / = 8,1 cm a uhol DBA je 42° - Kružnica vpísaná
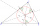 Je daný trojuholník ABC a kružnica vpísaná do tohto trojuholníka s polomerom 15. Bod T je bodom dotyku vpísanej kružnice so stranou BC. Aká je plocha trojuholníka ABC ak | BT | = 25 a | TC | = 26?
Je daný trojuholník ABC a kružnica vpísaná do tohto trojuholníka s polomerom 15. Bod T je bodom dotyku vpísanej kružnice so stranou BC. Aká je plocha trojuholníka ABC ak | BT | = 25 a | TC | = 26? - Trojuholníka 3511
 V trojuholníku s pravým uhlom pri vrchole C je uhol alfa o 24 stupňov menší ako uhol beta určite veľkosť uhlov trojuholníka.
V trojuholníku s pravým uhlom pri vrchole C je uhol alfa o 24 stupňov menší ako uhol beta určite veľkosť uhlov trojuholníka.
- Ťažnice v PT
 V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C sú dané veľkosti ťažníc ta=5, tb=2√10. Vypočítajte veľkosti strán trojuholníka ABC a polomer kružnice opísanej tomuto trojuholníku.
V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C sú dané veľkosti ťažníc ta=5, tb=2√10. Vypočítajte veľkosti strán trojuholníka ABC a polomer kružnice opísanej tomuto trojuholníku. - Trojuholníku 60423
 V pravouhlom trojuholníku RST s pravým uhlom pri vrchole T poznáme dĺžky dvoch strán: s = 7,8 cm a t = 13 cm; vypočítajte tretiu stranu r.
V pravouhlom trojuholníku RST s pravým uhlom pri vrchole T poznáme dĺžky dvoch strán: s = 7,8 cm a t = 13 cm; vypočítajte tretiu stranu r. - Pravouhlý
 Pravouhlý trojuholník KLM s pravým uhlom pri vrchole L, uhľom beta pri vrchole K a uhľom alfa u vrchole M. Uhol pri vrchole M = 65°, strana l = 17,5 cm. Pomôcť Pytagorovy vety a goniometrických funkciu vypočítate dĺžky všetkých strán a uhol pri vrchole K.
Pravouhlý trojuholník KLM s pravým uhlom pri vrchole L, uhľom beta pri vrchole K a uhľom alfa u vrchole M. Uhol pri vrchole M = 65°, strana l = 17,5 cm. Pomôcť Pytagorovy vety a goniometrických funkciu vypočítate dĺžky všetkých strán a uhol pri vrchole K.
