Planimetria - slovné úlohy a príklady - strana 145 z 177
Počet nájdených príkladov: 3524
- Lichobežník - uhly
 Lichobežníku s dĺžkou základne a = 36,6 cm sú ešte dané α = 60°, β = 48° a výška lichobežníka je 20 cm. Vypočítajte dĺžky ostatných strán lichobežníka.
Lichobežníku s dĺžkou základne a = 36,6 cm sú ešte dané α = 60°, β = 48° a výška lichobežníka je 20 cm. Vypočítajte dĺžky ostatných strán lichobežníka. - Súradnice priesečník
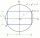 V pravouhlé sústave súradníc je narýsován obdĺžnik ABCD. Vrcholy obdĺžnika sú určené týmito súradnicami A = (2,2) B = (8,2) C = (8,6) D = (2,6) Určte súradnice priesečníka uhlopriečok obdĺžnika ABCD
V pravouhlé sústave súradníc je narýsován obdĺžnik ABCD. Vrcholy obdĺžnika sú určené týmito súradnicami A = (2,2) B = (8,2) C = (8,6) D = (2,6) Určte súradnice priesečníka uhlopriečok obdĺžnika ABCD - Eskalátor
 Pohyblivé schodisko sa pohybuje rýchlosťou veľkosti 0,6 m/s smerom nadol. Schodisko zviera s vodorovnou rovinou uhol 45°. Človek s hmotnosťou 80 kg kráča po schodisku smerom nahor rýchlosťou veľkosti 0,9 m/s. Určte dráhu, ktorú človek prejde a prácu, ktor
Pohyblivé schodisko sa pohybuje rýchlosťou veľkosti 0,6 m/s smerom nadol. Schodisko zviera s vodorovnou rovinou uhol 45°. Človek s hmotnosťou 80 kg kráča po schodisku smerom nahor rýchlosťou veľkosti 0,9 m/s. Určte dráhu, ktorú človek prejde a prácu, ktor - Výškový uhol
 Dopravné lietadlo, ktoré práve prelieta nad miestom 2 400 m vzdialenom od miesta pozorovateľa, je vidieť pod výškovým uhlom o veľkosti 26° 20 '. V akej výške lietadlo letí?
Dopravné lietadlo, ktoré práve prelieta nad miestom 2 400 m vzdialenom od miesta pozorovateľa, je vidieť pod výškovým uhlom o veľkosti 26° 20 '. V akej výške lietadlo letí? - Delostrelectvo 2
 Cieľ C pozorujú z dvoch delostreleckých pozorovateľní A, B navzájom vzdialených 296 m. Pritom uhol BAC = 52°42" a uhol ABC = 44°56". Vypočítajte vzdialenosť cieľa od pozorovateľne A.
Cieľ C pozorujú z dvoch delostreleckých pozorovateľní A, B navzájom vzdialených 296 m. Pritom uhol BAC = 52°42" a uhol ABC = 44°56". Vypočítajte vzdialenosť cieľa od pozorovateľne A. - Desaťuholníky - súčiastky
 Akú hmotnosť má 200 súčiastok o tvare pravidelného desaťuholníkov o strane 2 cm, ak je hmotnosť 1 m² plechu z ktorého sú vyrobené 24 kg?
Akú hmotnosť má 200 súčiastok o tvare pravidelného desaťuholníkov o strane 2 cm, ak je hmotnosť 1 m² plechu z ktorého sú vyrobené 24 kg? - Stred prepony
 Pre vnútorné uhly trojuholnika ABC platí, že alfa beta a gama sú v pomere 1:2:3. Najdlhšia strana trojuholníka AB má dĺžku 30cm. Vypočítaj obvod trojuholnika CBS, ak S je stred strany AB
Pre vnútorné uhly trojuholnika ABC platí, že alfa beta a gama sú v pomere 1:2:3. Najdlhšia strana trojuholníka AB má dĺžku 30cm. Vypočítaj obvod trojuholnika CBS, ak S je stred strany AB - Zorný uhol 2
 Pozorovateľ vidí priamu ohradu dlhú 60 m v zornom uhle 30°. Od jedného konca ohrady je vzdialený 102 m. Ako ďaleko je pozorovateľ od druhého konca ohrady?
Pozorovateľ vidí priamu ohradu dlhú 60 m v zornom uhle 30°. Od jedného konca ohrady je vzdialený 102 m. Ako ďaleko je pozorovateľ od druhého konca ohrady? - Lietadlo 12
 Lietadlo letí vo výške 22,5 km k pozorovateľni. V okamihu prvého merania ho bolo vidieť pod výškovým uhlom 28° a pri druhom meraní vo výškovom uhle 50°. Vypočítajte vzdialenosť, ktorú preletí medzi týmito dvomi meraniami.
Lietadlo letí vo výške 22,5 km k pozorovateľni. V okamihu prvého merania ho bolo vidieť pod výškovým uhlom 28° a pri druhom meraní vo výškovom uhle 50°. Vypočítajte vzdialenosť, ktorú preletí medzi týmito dvomi meraniami. - Šesťuholník S
 Vypočítajte obsah pravidelného šesťuholníka vpísaného do kružnice s polomerom r=16 cm.
Vypočítajte obsah pravidelného šesťuholníka vpísaného do kružnice s polomerom r=16 cm. - Šírka kanála
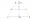 Priečny rez kanála má tvar lichobežníka. Šírka dna je 2,25 m a hĺbka 5 m. Steny majú sklon 68° 12' a 73° 45'. Vypočítajte hornú šírku kanála.
Priečny rez kanála má tvar lichobežníka. Šírka dna je 2,25 m a hĺbka 5 m. Steny majú sklon 68° 12' a 73° 45'. Vypočítajte hornú šírku kanála. - Ťažisko a obsah
 V trojuholníku ABC sú dané dĺžky jeho ťažníc tc=9, ta=6. Označme T priesečník ťažníc, S stred strany BC. Veľkosť uhla CTS je 60°. Vypočítajte dĺžku strany BC s presnosťou na 2 desatinné miesta
V trojuholníku ABC sú dané dĺžky jeho ťažníc tc=9, ta=6. Označme T priesečník ťažníc, S stred strany BC. Veľkosť uhla CTS je 60°. Vypočítajte dĺžku strany BC s presnosťou na 2 desatinné miesta - Stĺp elektrického vedenia
 Z miesta A je vidieť stĺp elektrického vedenia pod uhlom 18 stupňov. Z miesta B, do ktorého sa dostaneme, ideme Ak z Miesta A 30m smerom od stĺpu pod uhlom 10 stupňov. Urči výšku stĺpa elektrického vedenia.
Z miesta A je vidieť stĺp elektrického vedenia pod uhlom 18 stupňov. Z miesta B, do ktorého sa dostaneme, ideme Ak z Miesta A 30m smerom od stĺpu pod uhlom 10 stupňov. Urči výšku stĺpa elektrického vedenia. - V oblakoch
 Z dvoch miest A a B na vodorovnej rovine bolo pozorované čelo mraku nad spojnicou obidvoch miest pod výškovým uhlom 73°20' a 64°40'. Miesta A a B sú od seba vzdialené 2830 m. Ako vysoko je mrak?
Z dvoch miest A a B na vodorovnej rovine bolo pozorované čelo mraku nad spojnicou obidvoch miest pod výškovým uhlom 73°20' a 64°40'. Miesta A a B sú od seba vzdialené 2830 m. Ako vysoko je mrak? - Vysoká veža
 Z veže 15 metrov vysokej a od rieky 30 metrov vzdialenej sa javila šírka rieky v uhle 15°. Aká široká je rieka v tomto mieste?
Z veže 15 metrov vysokej a od rieky 30 metrov vzdialenej sa javila šírka rieky v uhle 15°. Aká široká je rieka v tomto mieste? - Funkcie sinus, kosinus
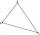 Vypočítaj veľkosti zostávajúcich strán a uhlov pravouhlého trojuholníka ABC, ak je dané: b = 10 cm; c = 20 cm; uhol alfa = 60° a uhol beta = 30° (použi Pytagorova vetu a funkcie sínus, kosínus, tangens, kotangens)
Vypočítaj veľkosti zostávajúcich strán a uhlov pravouhlého trojuholníka ABC, ak je dané: b = 10 cm; c = 20 cm; uhol alfa = 60° a uhol beta = 30° (použi Pytagorova vetu a funkcie sínus, kosínus, tangens, kotangens) - Šesťuholník rozdeľte
 Pravidelný šesťuholník rozdeľte úsečkami na deväť úplne zhodných dielov; žiadny z nich nesmie byť v zrkadlovom zobrazení (jednotlivé diely môžu byť iba ľubovoľne pootočené).
Pravidelný šesťuholník rozdeľte úsečkami na deväť úplne zhodných dielov; žiadny z nich nesmie byť v zrkadlovom zobrazení (jednotlivé diely môžu byť iba ľubovoľne pootočené). - Vrcholy trojuholníka
 Určte súradnice vrcholov trojúholníka ABC ak vieme stredy SAB [0;3] SBC [1;6] SAC [4;5], jeho strán AB, BC, AC.
Určte súradnice vrcholov trojúholníka ABC ak vieme stredy SAB [0;3] SBC [1;6] SAC [4;5], jeho strán AB, BC, AC. - Túra po hore
 Turista plánuje túru na jednu stranu hory a nadol na druhej strane vrcholu hory, pričom každá strana hory je tvorená priamkou. Uhol elevácie v počiatočnom bode je 42,4 stupňa a uhol elevácie na konci je 48,3 stupňa_ Horizontálna vzdialenosť medzi počiatoč
Turista plánuje túru na jednu stranu hory a nadol na druhej strane vrcholu hory, pričom každá strana hory je tvorená priamkou. Uhol elevácie v počiatočnom bode je 42,4 stupňa a uhol elevácie na konci je 48,3 stupňa_ Horizontálna vzdialenosť medzi počiatoč - Šarkany
 Chlapci si púšťali šarkana na šnúre 94 metrov dlhej. Ako vysoko poletuje šarkan, keď uhol od vodorovnej roviny je 47°?
Chlapci si púšťali šarkana na šnúre 94 metrov dlhej. Ako vysoko poletuje šarkan, keď uhol od vodorovnej roviny je 47°?
Máš príklad, ktorý si tu nenašiel vyriešenú? Pošli nám príklad a my Ti ho skúsime vypočítať.
