MO Z9-I-6 2019
Kristína zvolila isté nepárne prirodzené číslo deliteľné tromi. Jakub s Dávidom potom skúmali trojuholníky, ktoré majú obvod v milimetroch rovný Kristínou zvolenému číslu a ktorých strany majú dĺžky v milimetroch vyjadrené navzájom rôznymi celými číslami.
Jakub našiel taký trojuholník, v ktorom najdlhšia zo strán má najväčšiu možnú dĺžku, a túto hodnotu zapísal na tabuľu. Dávid našiel taký trojuholník, v ktorom najkratšia zo strán má najväčšiu možnú dĺžku, a túto hodnotu tiež zapísal na tabuľu. Kristína obe dĺžky na tabuli správne sčítala a vyšlo jej 1 681 mm. Určte, ktoré číslo Kristína zvolila.
Jakub našiel taký trojuholník, v ktorom najdlhšia zo strán má najväčšiu možnú dĺžku, a túto hodnotu zapísal na tabuľu. Dávid našiel taký trojuholník, v ktorom najkratšia zo strán má najväčšiu možnú dĺžku, a túto hodnotu tiež zapísal na tabuľu. Kristína obe dĺžky na tabuli správne sčítala a vyšlo jej 1 681 mm. Určte, ktoré číslo Kristína zvolila.
Správna odpoveď:

Tipy na súvisiace online kalkulačky
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Riešite Diofantovské problémy a hľadáte kalkulačku diofantovských celočíselných rovníc?
Chcete zaokrúhliť číslo?
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Riešite Diofantovské problémy a hľadáte kalkulačku diofantovských celočíselných rovníc?
Chcete zaokrúhliť číslo?
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Vypočítaj 440
 Vypočítaj v stupňoch veľkosť ostrého uhla, ktorý zvierajú ručičky hodín o pol šiestej.
Vypočítaj v stupňoch veľkosť ostrého uhla, ktorý zvierajú ručičky hodín o pol šiestej. - Určte 21
 Určte vzdialenosť dvoch neprístupných miest K, L, ak sa z bodov A, B, ktoré sú od seba vzdialené 870 m, namerali veľkosti uhlov KAL=62°10", LAB= 41°23", KBL=66°34", LBA= 34°52". Ďakujem.
Určte vzdialenosť dvoch neprístupných miest K, L, ak sa z bodov A, B, ktoré sú od seba vzdialené 870 m, namerali veľkosti uhlov KAL=62°10", LAB= 41°23", KBL=66°34", LBA= 34°52". Ďakujem. - Ťažnica na preponu
 Je daný pravouhly trojuholník KLM s pravým uhlom pri M. Aká je veľkosť prepony m, ak veľkosť tažnice na preponu m je 4.
Je daný pravouhly trojuholník KLM s pravým uhlom pri M. Aká je veľkosť prepony m, ak veľkosť tažnice na preponu m je 4. - Gotický
 Gotický štvorlístok je ornament, v ktorom sú do väčšej kružnice vpísané štyri rovnaké dotýkajúce sa menšie kružnice, ako vidíte na obrázku. Polomer veľkej kružnice je jeden meter. Vypočítajte v metroch polomer menšej kružnice.
Gotický štvorlístok je ornament, v ktorom sú do väčšej kružnice vpísané štyri rovnaké dotýkajúce sa menšie kružnice, ako vidíte na obrázku. Polomer veľkej kružnice je jeden meter. Vypočítajte v metroch polomer menšej kružnice.
- Štvoruholník 13
 Štvoruholník ABCD je súmerný podľa uhlopriečky AC. Dĺžka AC je 12 cm, dĺžka BC je 6 cm a vnútorný uhol pri vrchole B je pravý. na stranách AB, AD sú dané body E, F tak, že trojuholník ECF je rovnostranný. Určite dĺžku úsečky EF.
Štvoruholník ABCD je súmerný podľa uhlopriečky AC. Dĺžka AC je 12 cm, dĺžka BC je 6 cm a vnútorný uhol pri vrchole B je pravý. na stranách AB, AD sú dané body E, F tak, že trojuholník ECF je rovnostranný. Určite dĺžku úsečky EF. - Priesečník uhlopriečok
 Zostroj rovnobežník ABCD, ak a=5 cm, Výška na stranu a je 5 cm a uhol ASB = 120 stupňov. S je priesečník uhlopriečok.
Zostroj rovnobežník ABCD, ak a=5 cm, Výška na stranu a je 5 cm a uhol ASB = 120 stupňov. S je priesečník uhlopriečok. - Ostrouhlý trojuholník
 Daný je ostrouhlý trojuholník ABC. Na polpriamkach opačných k BA a CA ležia postupne body D a E tak, že |BD| = |AC| a |CE| = |AB|. Dokážte, že stred kružnice opísanej trojuholníku ADE leží na kružnici opísanej trojuholníku ABC.
Daný je ostrouhlý trojuholník ABC. Na polpriamkach opačných k BA a CA ležia postupne body D a E tak, že |BD| = |AC| a |CE| = |AB|. Dokážte, že stred kružnice opísanej trojuholníku ADE leží na kružnici opísanej trojuholníku ABC. - Na obrázku 5
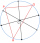 Na obrázku sú znázornené tri obce A, B, C a ich vzájomné vzdušné vzdialenosti. Nová priamočiara želežničná trať má byť postavená tak, aby zo všetkých obcí bolo k trati rovnako ďaleko a aby táto vzdialenosť bola najmenšia možná. Ako ďaleko budú od trate? a
Na obrázku sú znázornené tri obce A, B, C a ich vzájomné vzdušné vzdialenosti. Nová priamočiara želežničná trať má byť postavená tak, aby zo všetkých obcí bolo k trati rovnako ďaleko a aby táto vzdialenosť bola najmenšia možná. Ako ďaleko budú od trate? a - Daných
 Daných je 6 úsečiek s dĺžkami 3 cm, 4 cm, 5 cm, 7 cm, 8 cm a 9 cm. Koľko rôznostranných trojuholníkov sa z nich dá zostrojiť? Vypíš všetky možnosti.
Daných je 6 úsečiek s dĺžkami 3 cm, 4 cm, 5 cm, 7 cm, 8 cm a 9 cm. Koľko rôznostranných trojuholníkov sa z nich dá zostrojiť? Vypíš všetky možnosti.
- Trojuholníky
 Daný je štvorec ABCD a na každej jeho strane je zvolených n jej vnútorných bodov. Určte počet všetkých trojuholníkov, ktorých vrcholy X, Y, Z ležia v týchto bodoch a na rôznych stranách štvorca.
Daný je štvorec ABCD a na každej jeho strane je zvolených n jej vnútorných bodov. Určte počet všetkých trojuholníkov, ktorých vrcholy X, Y, Z ležia v týchto bodoch a na rôznych stranách štvorca. - Lietadlo 21
 Lietadlo letiace smerom k pozorovateľni, z nej bolo zamerané v priamej vzdialenosti 5300 m pod výškovým uhlom 28º a po 9 sekundách v priamej vzdialenosti 2400 m pod výškovým uhlom 50º. Vypočítajte vzdialenosť, ktorú v tomto časovom intervale lietadlo prel
Lietadlo letiace smerom k pozorovateľni, z nej bolo zamerané v priamej vzdialenosti 5300 m pod výškovým uhlom 28º a po 9 sekundách v priamej vzdialenosti 2400 m pod výškovým uhlom 50º. Vypočítajte vzdialenosť, ktorú v tomto časovom intervale lietadlo prel - Určte 9
 Určte vzdialenosť dvoch neprístupných miest P, Q, ak vzdialenosť dvoch pozorovacích miest A, B je 2000m a ak poznáte veľkosť uhlov QAB = 52°40'; PBA = 42°01'; PAB = 86°40' a QBA = 81°15'. Uvažované miesta A, B, P, Q ležia v jednej rovine.
Určte vzdialenosť dvoch neprístupných miest P, Q, ak vzdialenosť dvoch pozorovacích miest A, B je 2000m a ak poznáte veľkosť uhlov QAB = 52°40'; PBA = 42°01'; PAB = 86°40' a QBA = 81°15'. Uvažované miesta A, B, P, Q ležia v jednej rovine. - Urč veľkosť
 Urč veľkosť uhla ACF v pravidelnom 6-uholníku ABCDEF.
Urč veľkosť uhla ACF v pravidelnom 6-uholníku ABCDEF. - Rovnoramenný trojuholník 7
 Daných je 6 úsečiek s dĺžkami 3 cm, 4 cm, 5 cm, 7 cm, 8 cm, 9 cm, z každej dĺžky po dve. Koľko rovnoramenných trojuholníkov sa z nich dá zostrojiť? Vypíš všetky možnosti.
Daných je 6 úsečiek s dĺžkami 3 cm, 4 cm, 5 cm, 7 cm, 8 cm, 9 cm, z každej dĺžky po dve. Koľko rovnoramenných trojuholníkov sa z nich dá zostrojiť? Vypíš všetky možnosti.
- Podkrovie
 Nedávno som upratoval podkrovie a našiel som sadu najmenej 14 palíc, ktoré mi pred pár rokmi predal jeden zvedavý Talian. Keď som sa usilovne snažil prísť na to, prečo som to od neho kúpil, uvedomil som si, že sada má tú neuveriteľnú vlastnosť, že neexist
Nedávno som upratoval podkrovie a našiel som sadu najmenej 14 palíc, ktoré mi pred pár rokmi predal jeden zvedavý Talian. Keď som sa usilovne snažil prísť na to, prečo som to od neho kúpil, uvedomil som si, že sada má tú neuveriteľnú vlastnosť, že neexist - Zostroj
 Zostroj trojuholník ABC, ak je dané a+b+c (obvod), výška na stranu c a uhol gama.
Zostroj trojuholník ABC, ak je dané a+b+c (obvod), výška na stranu c a uhol gama. - Ťažnice zo súradníc
 Je daný trojuholník ABC: A[-6,6; 1,2], B[3,4; -5,6], C [2,8;4,2]. Vypočítajte dĺžky jeho ťažníc
Je daný trojuholník ABC: A[-6,6; 1,2], B[3,4; -5,6], C [2,8;4,2]. Vypočítajte dĺžky jeho ťažníc
