Lichobežník MO
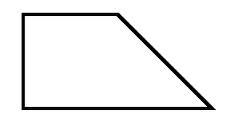
Je daný pravouhlý lichobežník ABCD s pravým uhlom pri bode B, |AC| = 12, |CD| = 8, uhlopriečky sú na seba kolmé.
Vypočítajte obvod a obsah takéhoto lichobežníka.
Vypočítajte obvod a obsah takéhoto lichobežníka.
Správna odpoveď:
Zobrazujem 2 komentáre:
Tipy na súvisiace online kalkulačky
Hľadáte pomoc s výpočtom koreňov kvadratickej rovnice?
Potrebujete pomôcť spočítať, vykrátiť či vynásobiť zlomky? Skúste našu zlomkovú kalkulačku.
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Potrebujete pomôcť spočítať, vykrátiť či vynásobiť zlomky? Skúste našu zlomkovú kalkulačku.
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- algebra
- kvadratická rovnica
- rovnica
- aritmetika
- odmocnina
- planimetria
- Pytagorova veta
- pravouhlý trojuholník
- obsah
- obvod
- trojuholník
- lichobežník
- uhlopriečka
- základné funkcie
- úvaha
- čísla
- zlomky
- goniometria a trigonometria
- sínus
- kosínus
- tangens
- arkustangens
- arkussínus
- arkuskosínus
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Anna malá
 Anna mala 3 krát viac ako Beátka. Cilka mala o 2 eura viac ako Beátka. Spolu mali 52 eur. Koľko mala každá?
Anna mala 3 krát viac ako Beátka. Cilka mala o 2 eura viac ako Beátka. Spolu mali 52 eur. Koľko mala každá? - Zamestnanci 4
 V sklade pracuje 21 zamestnancov - robotníkov a administratívnych pracovníkov. Pri úprave miezd znížili dennú odmenu každého administratívneho pracovníka o 3 € a dennú odmenu každého robotníka zvýšili o 2 €, takže celková denná mzda vzrástla o 17 €. Vypoč
V sklade pracuje 21 zamestnancov - robotníkov a administratívnych pracovníkov. Pri úprave miezd znížili dennú odmenu každého administratívneho pracovníka o 3 € a dennú odmenu každého robotníka zvýšili o 2 €, takže celková denná mzda vzrástla o 17 €. Vypoč - Jednotky, dvojky, trojky
 V triede je 30 žiakov. Piati mali známku trojku. Ostatní dvojky a jednotky. Priemer známok bol 1,9. Koľko žiakov malo jednotku?
V triede je 30 žiakov. Piati mali známku trojku. Ostatní dvojky a jednotky. Priemer známok bol 1,9. Koľko žiakov malo jednotku? - Pokladník 4
 Pokladník Samuel mal v pokladni spolu 20 ks bankoviek v celkovej hodnote 850 eur. Boli to iba 50 eurové a 20 eurové bankovky. Koľko kusov mal z každej bankovky?
Pokladník Samuel mal v pokladni spolu 20 ks bankoviek v celkovej hodnote 850 eur. Boli to iba 50 eurové a 20 eurové bankovky. Koľko kusov mal z každej bankovky?
- Trojuholníkov 83111
 Peťo zložil z navzájom zhodných trojuholníkov niekoľko rovinných útvarov. Obvody prvých troch sú postupne 8 cm, 11,4 cm a 14,7 cm. Určite obvod štvrtého útvaru
Peťo zložil z navzájom zhodných trojuholníkov niekoľko rovinných útvarov. Obvody prvých troch sú postupne 8 cm, 11,4 cm a 14,7 cm. Určite obvod štvrtého útvaru - Štvorčekových 83087
 Jana kúpila v papiernictve niekoľko rovnakých linajkových zošitov, niekoľko rovnakých štvorčekových zošitov a niekoľko rovnakých kružidiel. Dva linajkované zošity a dva štvorčekové zošity stoja dohromady 180 korún. Dva štvorčekové zošity stoja rovnako ako
Jana kúpila v papiernictve niekoľko rovnakých linajkových zošitov, niekoľko rovnakých štvorčekových zošitov a niekoľko rovnakých kružidiel. Dva linajkované zošity a dva štvorčekové zošity stoja dohromady 180 korún. Dva štvorčekové zošity stoja rovnako ako - Buchty 4
 Mama napiekla na večeru buchty. Otec zjedol z nich 1/3. Potom prišiel Jurko a zjedol štvrtinu zo zvyšných buchiet. Po Jurkovi prišiel Martin, ktorý zjedol tretinu zo zvyšných buchiet. Anka zjedla polovicu zostávajúcich buchiet a mame zostali štyri buchty.
Mama napiekla na večeru buchty. Otec zjedol z nich 1/3. Potom prišiel Jurko a zjedol štvrtinu zo zvyšných buchiet. Po Jurkovi prišiel Martin, ktorý zjedol tretinu zo zvyšných buchiet. Anka zjedla polovicu zostávajúcich buchiet a mame zostali štyri buchty. - 2x+3y-4=0 82676
 Napíšte rovnicu kružnice, ktorá prechádza bodmi Q[3,5], R[2,6] a má stred na priamke 2x+3y-4=0.
Napíšte rovnicu kružnice, ktorá prechádza bodmi Q[3,5], R[2,6] a má stred na priamke 2x+3y-4=0. - V základnej
 V základnej škole každoročne organizujú vedomostnú súťaž, v ktorej každý súťažiaci môže získať najviac 15 bodov. Tento rok bol priemerný bodový zisk súťažiacich zaokrúhlený na desatiny rovný 10,4. Jožko si po súťaži uvedomil, že niek
V základnej škole každoročne organizujú vedomostnú súťaž, v ktorej každý súťažiaci môže získať najviac 15 bodov. Tento rok bol priemerný bodový zisk súťažiacich zaokrúhlený na desatiny rovný 10,4. Jožko si po súťaži uvedomil, že niek
- Uvedených 82574
 Do krúžku chodí 29 detí. 11 uviedlo, že má doma psa, 14 detí má doma mačku a 12 detí má doma škrečka. Dve deti majú všetky tri zvieratká. 7 detí nemá doma žiadne zviera. . Koľko detí má aspoň dve z uvedených zvierat? Koľko detí má práve jedno z uvedených
Do krúžku chodí 29 detí. 11 uviedlo, že má doma psa, 14 detí má doma mačku a 12 detí má doma škrečka. Dve deti majú všetky tri zvieratká. 7 detí nemá doma žiadne zviera. . Koľko detí má aspoň dve z uvedených zvierat? Koľko detí má práve jedno z uvedených - Predajca 3
 Predajca chcel predať 100 lacnejších a 50 drahších mobilov. Cenový rozdiel medzi lacnejším a drahším mobilom je 30 eur. Pôvodne chcel predať každý lacnejší so zľavou 20% a drahší so zľavou 12%. Nakoniec sa rozhodol, že lacnejšie predá so zľavou 40% a drah
Predajca chcel predať 100 lacnejších a 50 drahších mobilov. Cenový rozdiel medzi lacnejším a drahším mobilom je 30 eur. Pôvodne chcel predať každý lacnejší so zľavou 20% a drahší so zľavou 12%. Nakoniec sa rozhodol, že lacnejšie predá so zľavou 40% a drah - Skautskom MO 2023 z8
 V minulom roku bolo v našom skautskom oddiele o 30 chlapcov viac ako dievčat. Tento rok sa počet detí v oddiele zväčšil o 10%, pričom počet chlapcov sa zväčšil o 5% a počet dievčat sa zväčšil o 20%. Koľko detí máme tento rok v oddiele?
V minulom roku bolo v našom skautskom oddiele o 30 chlapcov viac ako dievčat. Tento rok sa počet detí v oddiele zväčšil o 10%, pričom počet chlapcov sa zväčšil o 5% a počet dievčat sa zväčšil o 20%. Koľko detí máme tento rok v oddiele? - Ružových
 Ružových lekien je v jazierku dvakrát viac ako žltých, ale dvakrát menej ako bielych. Ktorých lekien je najviac a ktorých najmenej. Koľko krát viac je bielich lekien ako žltých. Koľko je ružových lekien, ak všetkých je 35?
Ružových lekien je v jazierku dvakrát viac ako žltých, ale dvakrát menej ako bielych. Ktorých lekien je najviac a ktorých najmenej. Koľko krát viac je bielich lekien ako žltých. Koľko je ružových lekien, ak všetkých je 35? - Kružitiek 81839
 K nákupu šiestich kružitiek chýbalo Jane 160 korún, preto kúpila iba štyri a zostalo ju 100 korún. Koľko stoja 4 krúžitka?
K nákupu šiestich kružitiek chýbalo Jane 160 korún, preto kúpila iba štyri a zostalo ju 100 korún. Koľko stoja 4 krúžitka?
- Eva zaplatila
 Eva zaplatila za tri venčeky a päť krémešov 8,4 €. Jana zaplatila za 9 venčekov a 7 krémešov 15,6 €. Koľko korún bude platiť Janko za jeden venček a jeden krémeš?
Eva zaplatila za tri venčeky a päť krémešov 8,4 €. Jana zaplatila za 9 venčekov a 7 krémešov 15,6 €. Koľko korún bude platiť Janko za jeden venček a jeden krémeš? - Zuzke
 Zuzke sa z poslednej písomky podarilo získať 40 bodov zo 60 možných. Jej priemerný počet bodov z písomiek tým vzrástol zo 27 na 28 bodov. Na koľko bodov ju mala napísať, ak chcela, aby jej celkový priemer vzrástol až na 29 bodov?
Zuzke sa z poslednej písomky podarilo získať 40 bodov zo 60 možných. Jej priemerný počet bodov z písomiek tým vzrástol zo 27 na 28 bodov. Na koľko bodov ju mala napísať, ak chcela, aby jej celkový priemer vzrástol až na 29 bodov? - V mliekarni 2
 V mliekarni majú dve linky na plnenie škatúľ mlieka. Modernejšia linka je jeden a pol-krát rýchlejšia, ako stará linka. Keď pracujú obe linky súčasne, naplnia bežné denné množstvo škatúľ mlieka o 5 hodín skôr, ako keď pracovala iba stará linka. Vypočítajt
V mliekarni majú dve linky na plnenie škatúľ mlieka. Modernejšia linka je jeden a pol-krát rýchlejšia, ako stará linka. Keď pracujú obe linky súčasne, naplnia bežné denné množstvo škatúľ mlieka o 5 hodín skôr, ako keď pracovala iba stará linka. Vypočítajt
