Kvadratická rovnica - stredná škola - príklady a úlohy
Počet nájdených príkladov: 430
- Určte 22
 Určte hodnotu čísla a tak, aby grafy funkcií f: y = x² a g: y = 2x + a mali spoločný práve jeden bod.
Určte hodnotu čísla a tak, aby grafy funkcií f: y = x² a g: y = 2x + a mali spoločný práve jeden bod. - Maturitný príklad
 Obsah lichobežníka je 132cm². Rozdiel dĺžok oboch základní je 6cm, výška je o 2cm dlhšia ako kratšia základňa. Určte v centimetroch veľkosť výšky lichobežníka.
Obsah lichobežníka je 132cm². Rozdiel dĺžok oboch základní je 6cm, výška je o 2cm dlhšia ako kratšia základňa. Určte v centimetroch veľkosť výšky lichobežníka. - Vypočítajte 257
 Vypočítajte súčet x-ových súradníc priesečníkov kružnice danej rovnicou (x - 1)²+ y² = 1 a priamky danej parametricky x = t, y = t , kde t∈R.
Vypočítajte súčet x-ových súradníc priesečníkov kružnice danej rovnicou (x - 1)²+ y² = 1 a priamky danej parametricky x = t, y = t , kde t∈R. - Rovnobežník TTT
 Vypočítajte obsah rovnobežníka, ak poznáme obvod je 23 cm, uhlopriečka je 8,5cm a jedna strana je o 1,5cm dlhšia.
Vypočítajte obsah rovnobežníka, ak poznáme obvod je 23 cm, uhlopriečka je 8,5cm a jedna strana je o 1,5cm dlhšia.
- Pri úprave 2
 Pri úprave školského pozemku, v tvare obdĺžnika, deviataci vypočítali ak zväčšíme dĺžku aj šírku pozemku o 1m zväčšíme jeho výmeru o 22m². Ak zmenšime dĺžku pozemku o 2m a zväčšíme jeho šírku o 1m zmenší sa jeho výmera o 5m². Aká je výmera školského pozem
Pri úprave školského pozemku, v tvare obdĺžnika, deviataci vypočítali ak zväčšíme dĺžku aj šírku pozemku o 1m zväčšíme jeho výmeru o 22m². Ak zmenšime dĺžku pozemku o 2m a zväčšíme jeho šírku o 1m zmenší sa jeho výmera o 5m². Aká je výmera školského pozem - Kvadratická rovnica korene
 V rovnici 3x²+bx+c=0 je jeden koreň x1 = -3/2. Určite číslo c tak, aby číslo 4 bolo koreňom rovnice. Nápoveda - použite Vietove vzorce.
V rovnici 3x²+bx+c=0 je jeden koreň x1 = -3/2. Určite číslo c tak, aby číslo 4 bolo koreňom rovnice. Nápoveda - použite Vietove vzorce. - Ohnisko a priamka
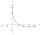 Určte rovnicu paraboly, ktorá má bod F = [3,2] za svoje ohnisko a priamku x+y+1=0 za svoju radiacu priamku.
Určte rovnicu paraboly, ktorá má bod F = [3,2] za svoje ohnisko a priamku x+y+1=0 za svoju radiacu priamku. - Aké strany
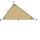 Aké strany má pravouhlý trojuholník s obvodom 45 centimetrov a s obsahom 67,5 cm²?
Aké strany má pravouhlý trojuholník s obvodom 45 centimetrov a s obsahom 67,5 cm²? - Objekt
 Objekt má rýchlosť 25m/s, zrýchľuje 5,0m/s² na 250 metrov. Aká je konečná rýchlosť?
Objekt má rýchlosť 25m/s, zrýchľuje 5,0m/s² na 250 metrov. Aká je konečná rýchlosť?
- Určte 17
 Určte s5 geometrickej postupnosti, ak platí: a1 + a2 = 10 a a4 - a2 = 120
Určte s5 geometrickej postupnosti, ak platí: a1 + a2 = 10 a a4 - a2 = 120 - Mnohouholník strany
 Určte druh mnohouholníka, ak je počet všetkých uhlopriečok 90. (Zapíšte počet jeho strán)
Určte druh mnohouholníka, ak je počet všetkých uhlopriečok 90. (Zapíšte počet jeho strán) - Gotický
 Gotický štvorlístok je ornament, v ktorom sú do väčšej kružnice vpísané štyri rovnaké dotýkajúce sa menšie kružnice, ako vidíte na obrázku. Polomer veľkej kružnice je jeden meter. Vypočítajte v metroch polomer menšej kružnice.
Gotický štvorlístok je ornament, v ktorom sú do väčšej kružnice vpísané štyri rovnaké dotýkajúce sa menšie kružnice, ako vidíte na obrázku. Polomer veľkej kružnice je jeden meter. Vypočítajte v metroch polomer menšej kružnice. - Funkce parabolická
 Je dána funkce y = x² - 4x + 3 Určete všechna reálná čísla z tak, aby platilo g(x) = g(-2).
Je dána funkce y = x² - 4x + 3 Určete všechna reálná čísla z tak, aby platilo g(x) = g(-2). - Vyjadrenie 82991
 Prosím o vyjadrenie r zo vzorca pre povrch valca.
Prosím o vyjadrenie r zo vzorca pre povrch valca.
- Najvzdialenejšieho 82855
 Pomer vzdialenosti najbližšieho a najvzdialenejšieho bodu kružnice, ktorá je popísaná rovnicou x2+y2-16x-12y+75=0 od začiatku sústavy súradníc je?
Pomer vzdialenosti najbližšieho a najvzdialenejšieho bodu kružnice, ktorá je popísaná rovnicou x2+y2-16x-12y+75=0 od začiatku sústavy súradníc je? - -2x-4y-20=0 82677
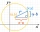 Určite súradnice vrcholu obdĺžnika vpísaného do kružnice x²+y² -2x-4y-20=0, ak viete, že jedna jeho strana leží na priamke p: x+2y=0
Určite súradnice vrcholu obdĺžnika vpísaného do kružnice x²+y² -2x-4y-20=0, ak viete, že jedna jeho strana leží na priamke p: x+2y=0 - Činitele 82564
 Súčin dvoch celých čisel, z ktorých jedno je o 19 väčší ako druhé, je roveň číslu 416. Nájdete oba činitele.
Súčin dvoch celých čisel, z ktorých jedno je o 19 väčší ako druhé, je roveň číslu 416. Nájdete oba činitele. - Prechádza 82394
 Určite rovnicu kružnice, ktorá prechádza bodom M(-1,2) a N( 3,0) a ktorej stred leží na priamke p: x=-3+t, y=-1+t,
Určite rovnicu kružnice, ktorá prechádza bodom M(-1,2) a N( 3,0) a ktorej stred leží na priamke p: x=-3+t, y=-1+t, - Spracovanie 82207
 Kvôli veľkej úrode zemiakov tento rok prikúpili na statku k starej triedičke novú, výkonnejšiu. Teraz pracujú oba stroje súčasne, a preto je denný zber spracovaný za 12 hodín. Keby pracoval iba starý stroj, potreboval by na spracovanie denného zberu o 10
Kvôli veľkej úrode zemiakov tento rok prikúpili na statku k starej triedičke novú, výkonnejšiu. Teraz pracujú oba stroje súčasne, a preto je denný zber spracovaný za 12 hodín. Keby pracoval iba starý stroj, potreboval by na spracovanie denného zberu o 10
Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať.
