Podstava
Podstavu kolmého hranola tvorí pravouhlý trojuholník, ktorého odvesny majú pomer 3:4. Výška hranola je o 2cm menšia, ako väčšia odvesna. Určite objem hranola, ak jeho povrch je 468 cm2.
Správna odpoveď:

Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- algebra
- vyjadrenie neznámej zo vzorca
- stereometria
- povrch telesa
- hranol
- planimetria
- Pytagorova veta
- pravouhlý trojuholník
- obsah
- trojuholník
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Kruh odsek/úsek
 Kruh s priemerom 30 cm je preťať tetivou t = 16 cm. Vypočítajte obvod a obsah menšieho odseku.
Kruh s priemerom 30 cm je preťať tetivou t = 16 cm. Vypočítajte obvod a obsah menšieho odseku. - Objem 41
 Objem pravidelného štvorbokého ihlanu je 72 cm³.Jeho výška sa rovná dĺžke podstavnej hrany. Vypočítaj dĺžku podstavnej a povrch ihlana.
Objem pravidelného štvorbokého ihlanu je 72 cm³.Jeho výška sa rovná dĺžke podstavnej hrany. Vypočítaj dĺžku podstavnej a povrch ihlana. - Polovica obĺžnika
 Vypočítajte obsah pravouhlého trojuholníka ABC s odvesnami a=15cm, b=1,7dm.
Vypočítajte obsah pravouhlého trojuholníka ABC s odvesnami a=15cm, b=1,7dm. - Výška, uhol a strana
 Vypočítajte obsah trojuholníka ABC, v ktorom poznáte stranu c=5 cm, uhol pri vrchole A= 70 stupňov a pomer úsekov, ktoré vytína výška na stranu c je 1:3.
Vypočítajte obsah trojuholníka ABC, v ktorom poznáte stranu c=5 cm, uhol pri vrchole A= 70 stupňov a pomer úsekov, ktoré vytína výška na stranu c je 1:3.
- Rovnoramenný trojuholník -VU
 Vypočítajte dĺžky strán v rovnoramennom trojuholníku, ak je dana výška (na základňu) Vc= 8,8cm a uhol pri zakladni alfa= 38°40`.
Vypočítajte dĺžky strán v rovnoramennom trojuholníku, ak je dana výška (na základňu) Vc= 8,8cm a uhol pri zakladni alfa= 38°40`. - Tetiva - uhol
 Je daná kružnica k so stredom v bode S a polomerom 6 cm. Vypočítaj veľkosť stredového uhla, ktorý patí tetive dlhej 10 cm.
Je daná kružnica k so stredom v bode S a polomerom 6 cm. Vypočítaj veľkosť stredového uhla, ktorý patí tetive dlhej 10 cm. - Z drevenej 2
 Z drevenej plátne tvár obdĺžnika s rozmermi 80 CM a 65 CM odrezal stolár pravoúhly trojuholník s voľnými stranami 550 mm a 200 mm. kolko centimetrov štvorcových bude tvoriť odpad?
Z drevenej plátne tvár obdĺžnika s rozmermi 80 CM a 65 CM odrezal stolár pravoúhly trojuholník s voľnými stranami 550 mm a 200 mm. kolko centimetrov štvorcových bude tvoriť odpad? - Obsah 44
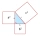 Obsah pravouhlému trojuholníka ABC je 346 cm² a uhol pri vrchole A je 64°. Vypočítajte dĺžky odvesien a, b.
Obsah pravouhlému trojuholníka ABC je 346 cm² a uhol pri vrchole A je 64°. Vypočítajte dĺžky odvesien a, b. - Ťažnice v PT
 V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C sú dané veľkosti ťažníc ta=5, tb=2√10. Vypočítajte veľkosti strán trojuholníka ABC a polomer kružnice opísanej tomuto trojuholníku.
V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C sú dané veľkosti ťažníc ta=5, tb=2√10. Vypočítajte veľkosti strán trojuholníka ABC a polomer kružnice opísanej tomuto trojuholníku.
- Záhrada 41
 Záhrada má tvar pravoúhleho lichobežníka a=50m, c=30m, d=15m. Koľko metrov pletiva potrebujeme na jej oplotenie, ak musíme k vypčíitanej dĺžke pripočítať 8% stratu?
Záhrada má tvar pravoúhleho lichobežníka a=50m, c=30m, d=15m. Koľko metrov pletiva potrebujeme na jej oplotenie, ak musíme k vypčíitanej dĺžke pripočítať 8% stratu? - Rebrík 15
 Rebrík dlhý 6,5 m je opretý o zvislú stenu. Jeho spodný koniec sa opiera o zem vo vzdialenosti 1,6 m od steny. Určte, do akej výšky dosahuje horný koniec rebríka a pod akým uhlom je rebrík opretý o stenu.
Rebrík dlhý 6,5 m je opretý o zvislú stenu. Jeho spodný koniec sa opiera o zem vo vzdialenosti 1,6 m od steny. Určte, do akej výšky dosahuje horný koniec rebríka a pod akým uhlom je rebrík opretý o stenu. - Deltoid 2
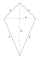 Papierový šarkan má tvar deltoidu ABCD, v ktorom sú dve kratšie strany dlhé po 30 cm, dve dlhšie strany po 51 cm a kratšia uhlopriečka má dĺžku 48 cm. Určte veľkosti vnútorných uhlov daného deltoidu.
Papierový šarkan má tvar deltoidu ABCD, v ktorom sú dve kratšie strany dlhé po 30 cm, dve dlhšie strany po 51 cm a kratšia uhlopriečka má dĺžku 48 cm. Určte veľkosti vnútorných uhlov daného deltoidu. - Kocka 65
 Kocka je zložená zo 64 malých kociek z ktorých každá má dĺžku hrany 15 mm. Vypočítaj dĺžku stenovej a telesovej uhlopriečky.
Kocka je zložená zo 64 malých kociek z ktorých každá má dĺžku hrany 15 mm. Vypočítaj dĺžku stenovej a telesovej uhlopriečky. - Výška
 Výška je nakreslená z vrcholu rovnoramenného trojuholníka, ktorý tvorí pravý uhol a dva zhodné trojuholníky. Výsledkom je, že výška rozdeľuje základňu na dva rovnaké segmenty. Dĺžka výšky je 18 palcov a dĺžka základne je 15 palcov. Nájdite obvod trojuholn
Výška je nakreslená z vrcholu rovnoramenného trojuholníka, ktorý tvorí pravý uhol a dva zhodné trojuholníky. Výsledkom je, že výška rozdeľuje základňu na dva rovnaké segmenty. Dĺžka výšky je 18 palcov a dĺžka základne je 15 palcov. Nájdite obvod trojuholn
- Rebrík 14
 Rebrík dĺžky 3,4 m je opretý o stenu. Jeho dolný koniec je od steny vzdialeny 1,6m. V akej výške sa rebrík dotýka steny?
Rebrík dĺžky 3,4 m je opretý o stenu. Jeho dolný koniec je od steny vzdialeny 1,6m. V akej výške sa rebrík dotýka steny? - Ako zistím
 Ako zistím uhlopriečky kosoštvorca, ak jeho obvod je 80dm a jedna uhlopriečka je 2x väčšia ako druhá?
Ako zistím uhlopriečky kosoštvorca, ak jeho obvod je 80dm a jedna uhlopriečka je 2x väčšia ako druhá? - Na vrchole 2
 Na vrchole kopca stojí rozhľadňa 30 m vysoká. Jej pätu a vrchol vidíme z určitého miesta v údolí pod výškovými uhlami a= 28°30", b=30°40". Ako vysoko je vrchol kopca nad horizontálnou rovinou pozorovacieho miesta?
Na vrchole kopca stojí rozhľadňa 30 m vysoká. Jej pätu a vrchol vidíme z určitého miesta v údolí pod výškovými uhlami a= 28°30", b=30°40". Ako vysoko je vrchol kopca nad horizontálnou rovinou pozorovacieho miesta?
