Prodlouží-li
Prodlouží-li se délky hran krychle o 5 cm, zvětší se její objem o 485 cm3. Určete povrch původní i zvětšené krychle.
Správná odpověď:
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Rozřezal 4283
 Alex rozřezal jedním řezem dřevěný kvádr na dvě části. Které těleso nemohl dostat?
Alex rozřezal jedním řezem dřevěný kvádr na dvě části. Které těleso nemohl dostat? - Pilíř 3
 Kolik betonu je třeba na vylití 8 betonových sloupů s podstavou čtverce: a = 38cm, výška sloupů je 6,2m? V každém sloupu je dutina válce o průměru 15cm.
Kolik betonu je třeba na vylití 8 betonových sloupů s podstavou čtverce: a = 38cm, výška sloupů je 6,2m? V každém sloupu je dutina válce o průměru 15cm. - Vypočítejte 248
 Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66°
Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66° - Do koule
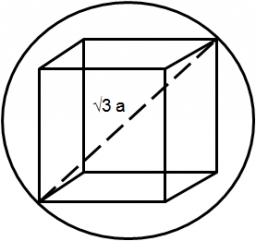
 Do koule o poloměru 27 cm je vepsána krychle. Vypočtěte její objem a povrch.
Do koule o poloměru 27 cm je vepsána krychle. Vypočtěte její objem a povrch.
- Vypočítejte 70294
 Délky hran čtyřbokého hranolu jsou v poměru a: b:c = 2:4:5. Povrch hranolu je 57 cm². Vypočítejte objem.
Délky hran čtyřbokého hranolu jsou v poměru a: b:c = 2:4:5. Povrch hranolu je 57 cm². Vypočítejte objem. - Krabice na mléko
 Monika si změřila rozměry dvou různých krabic na mléko. Jedna měla rozměry 9*5,8*19,6 cm, druhá 9,4*6,3*17,3 cm. Zaujalo ji, zda se na výrobu některé krabice spotřebuje méně materiálu. Ověř to a zjisti, kolik procent materiálu se ušetří. (Materiál na zalo
Monika si změřila rozměry dvou různých krabic na mléko. Jedna měla rozměry 9*5,8*19,6 cm, druhá 9,4*6,3*17,3 cm. Zaujalo ji, zda se na výrobu některé krabice spotřebuje méně materiálu. Ověř to a zjisti, kolik procent materiálu se ušetří. (Materiál na zalo - Roviny bočních stěn
 Vypočítej objem a povrch kvádru jehož strana c má délku 30 cm a tělesová úhlopříčka svírá s rovinami bočních stěn úhly o velikostech 24 st. 20’, 45 st. 30’
Vypočítej objem a povrch kvádru jehož strana c má délku 30 cm a tělesová úhlopříčka svírá s rovinami bočních stěn úhly o velikostech 24 st. 20’, 45 st. 30’ - Pod koulí
 Kolmý kruhový kužel s horní šířkou 24 cm a výškou 8 cm je naplněn vodou. V kuželu je ponořena kulová ocelová koule o poloměru 3,0 cm. Najděte objem vody pod koulí.
Kolmý kruhový kužel s horní šířkou 24 cm a výškou 8 cm je naplněn vodou. V kuželu je ponořena kulová ocelová koule o poloměru 3,0 cm. Najděte objem vody pod koulí. - Seříznutého 58663
 Ocelovou součástku ve tvaru seříznutého čtyřbokého jehlanu roztavili a vyrobili tři identické kostky. Určete povrch jedné kostky, pokud hrany postav jehlanu jsou 30 mm a 80 mm a výška jehlanu je 60 mm. Nevím si s tím nijak rády, nenašel jsem nikde řešení
Ocelovou součástku ve tvaru seříznutého čtyřbokého jehlanu roztavili a vyrobili tři identické kostky. Určete povrch jedné kostky, pokud hrany postav jehlanu jsou 30 mm a 80 mm a výška jehlanu je 60 mm. Nevím si s tím nijak rády, nenašel jsem nikde řešení
- Objem
 Objem pravidelného čtyřbokého hranolu je 192 cm³. Velikost jeho podstavné hrany a tělesových výšky jsou v poměru 1:3. Vypočítejte povrch hranolu.
Objem pravidelného čtyřbokého hranolu je 192 cm³. Velikost jeho podstavné hrany a tělesových výšky jsou v poměru 1:3. Vypočítejte povrch hranolu. - Konvexní
 Konvexní čočka se skládá ze dvou kulových úsečí (rozměry zadány v mm). Vypočítejte její hmotnost, je-li hustota skla 2,5 g/cm³. Rozměry: 60mm na délku a šiřka vrchní části 5mm, šířka spodni časti 8mm
Konvexní čočka se skládá ze dvou kulových úsečí (rozměry zadány v mm). Vypočítejte její hmotnost, je-li hustota skla 2,5 g/cm³. Rozměry: 60mm na délku a šiřka vrchní části 5mm, šířka spodni časti 8mm - Vejce napoly
 V dřevěné polokouli s poloměrem r=1 byla vytvořena prohlubeň tvaru polokoule s poloměrem r/2 tak, že podstavy obou polokoulí leží v téže rovině. Jaký je povrch vytvořeného tělesa (včetně plochy prohlubně)?
V dřevěné polokouli s poloměrem r=1 byla vytvořena prohlubeň tvaru polokoule s poloměrem r/2 tak, že podstavy obou polokoulí leží v téže rovině. Jaký je povrch vytvořeného tělesa (včetně plochy prohlubně)? - Kulová vrstva, úseč
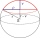 Vypočtěte objem kulové vrstvy, která zůstane z polokoule po odříznutí úseče s výškou 3 cm. Výška polokoule je 10 cm.
Vypočtěte objem kulové vrstvy, která zůstane z polokoule po odříznutí úseče s výškou 3 cm. Výška polokoule je 10 cm. - Vypočítej 39
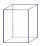 Vypočítej objem (V) a povrch (S) pravidelného čtyřbokého hranolu, jehož výška je 28,6 cm a odchylka tělesové úhlopříčky od roviny podlahy je 50°.
Vypočítej objem (V) a povrch (S) pravidelného čtyřbokého hranolu, jehož výška je 28,6 cm a odchylka tělesové úhlopříčky od roviny podlahy je 50°.
- Kopule
 Kopule hvězdárny se tvarem blíží polokouli. Její vnější průměr je 11 m. Kolik kilogramů barvy a kolik litrů ředidla se spotřebuje na její dvojitý nátěr, víte-li, že 1 kilogramem barvy rozředěným 1 decilitrem ředidla se natře plocha s obsahem 7,3 m².
Kopule hvězdárny se tvarem blíží polokouli. Její vnější průměr je 11 m. Kolik kilogramů barvy a kolik litrů ředidla se spotřebuje na její dvojitý nátěr, víte-li, že 1 kilogramem barvy rozředěným 1 decilitrem ředidla se natře plocha s obsahem 7,3 m². - Dřevěná
 Dřevěná nádoba tvaru krychle má uvnitř pokrýt plechem. Venkovni hrana nádoby je 54cm. Hrubky stěny je 25 mm. Nádoba nemá víko. Vypočtěte. Kolik plechu bude nutné na její pokryti?
Dřevěná nádoba tvaru krychle má uvnitř pokrýt plechem. Venkovni hrana nádoby je 54cm. Hrubky stěny je 25 mm. Nádoba nemá víko. Vypočtěte. Kolik plechu bude nutné na její pokryti? - Na válec
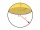 Na válec o průměru 4,6 cm nasaďte část koule tak, aby povrch této části byl 20 cm². Určete r koule ze které byl vrchlík seříznut.
Na válec o průměru 4,6 cm nasaďte část koule tak, aby povrch této části byl 20 cm². Určete r koule ze které byl vrchlík seříznut.
