Hranol X
Hranol s hranami o dĺžkach x cm, 2x cm a 3x cm a má objem 48000 cm3.
Akú veľkosť má povrch tohto hranola?
Akú veľkosť má povrch tohto hranola?
Správna odpoveď:

Tipy na súvisiace online kalkulačky
Chcete premeniť jednotku dĺžky?
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- algebra
- vyjadrenie neznámej zo vzorca
- aritmetika
- tretia odmocnina
- odmocnina
- tretia mocnina
- umocňovanie
- stereometria
- kváder
- povrch telesa
- hranol
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Typ rádioaktívneho
 Typ rádioaktívneho prvku má hmotnosť 1,125 gramu. Pri analýze sa zistí, že má 405 rokov. Ak sa tento rádioaktívny prvok každých 45 rokov rozpadne o polovicu, zistite, koľko gramov tohto rádioaktívneho prvku bolo pred 405 rokmi.
Typ rádioaktívneho prvku má hmotnosť 1,125 gramu. Pri analýze sa zistí, že má 405 rokov. Ak sa tento rádioaktívny prvok každých 45 rokov rozpadne o polovicu, zistite, koľko gramov tohto rádioaktívneho prvku bolo pred 405 rokmi. - Sedemsegmantovka
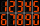 Elektronické zariadenia niekedy používajú nižšie uvedený typ číslic - sedemsegmentovku, kde každá číslica používa niekoľko krátkych svietiacich prúžkov, napríklad sedem používa tri malé prúžky. Aké je najväčšie trojciferné číslo, ktoré môžete vytvoriť, ak
Elektronické zariadenia niekedy používajú nižšie uvedený typ číslic - sedemsegmentovku, kde každá číslica používa niekoľko krátkych svietiacich prúžkov, napríklad sedem používa tri malé prúžky. Aké je najväčšie trojciferné číslo, ktoré môžete vytvoriť, ak - V=4x^3+43x^2+63x 72764
 Najväčšie vnútorné akvárium na svete. Vo svojej obrovskej nádrži s kapacitou reprezentovanou nasledujúcim polynómom V=4x³+43x²+63x Akvárium má tvar obdĺžnikového hranola. Nájdite nasledovné: 1. Ak je výška akvária x, nájdite plochu základne (B). 2. Na zák
Najväčšie vnútorné akvárium na svete. Vo svojej obrovskej nádrži s kapacitou reprezentovanou nasledujúcim polynómom V=4x³+43x²+63x Akvárium má tvar obdĺžnikového hranola. Nájdite nasledovné: 1. Ak je výška akvária x, nájdite plochu základne (B). 2. Na zák - Konečná GP
 Určte zvyšné veličiny v konečnej geometrickej postupnosti, ak je dané: a1=18, an=13122, sn=19674, n=?, q=?
Určte zvyšné veličiny v konečnej geometrickej postupnosti, ak je dané: a1=18, an=13122, sn=19674, n=?, q=?
- Poseidon
 Poseidon vložil 2 747 zlatých drachiem na sporiaci účet univerzity Mount Olympus, aby zabezpečil, že Percy môže ísť na vysokú školu. Platí ročné úroky 0,04 (v desatinnej podobe). Po 11 rokoch vyberie peniaze. O koľko viac peňazí by mal, keby sa úrok vyplá
Poseidon vložil 2 747 zlatých drachiem na sporiaci účet univerzity Mount Olympus, aby zabezpečil, že Percy môže ísť na vysokú školu. Platí ročné úroky 0,04 (v desatinnej podobe). Po 11 rokoch vyberie peniaze. O koľko viac peňazí by mal, keby sa úrok vyplá - Počet obyvateľov
 Počet obyvateľov mesta je 56 000. Každý rok klesá o 2%. Aký bude počet obyvateľov mesta po 13 rokoch?
Počet obyvateľov mesta je 56 000. Každý rok klesá o 2%. Aký bude počet obyvateľov mesta po 13 rokoch? - Ročný prírastok
 Počet vyrobených aut vzrástol za 3 roky z 45 000 na 47 000. Vypočítajte, aký bol priemerný ročný prírastok aut v %.
Počet vyrobených aut vzrástol za 3 roky z 45 000 na 47 000. Vypočítajte, aký bol priemerný ročný prírastok aut v %. - Percentuálny 36383
 Na stránkach ČSÚ sa môžeme dozvedieť, že v roku 1869 mala Praha aj s predmestiami celkom 10 947 domov av roku 1900 už 18 838 domov. Aký bol každoročný percentuálny „prírastok“ domov v Prahe medzi rokmi 1869 až 1900, ak uvažujeme konštantný percentuálny „p
Na stránkach ČSÚ sa môžeme dozvedieť, že v roku 1869 mala Praha aj s predmestiami celkom 10 947 domov av roku 1900 už 18 838 domov. Aký bol každoročný percentuálny „prírastok“ domov v Prahe medzi rokmi 1869 až 1900, ak uvažujeme konštantný percentuálny „p - GP - členy
 Aký je 5. člen geometrickej postupnosti, ak je 8. člen 80 a spoločný pomer (kvocient) r = 1/2?
Aký je 5. člen geometrickej postupnosti, ak je 8. člen 80 a spoločný pomer (kvocient) r = 1/2?
- Percentuálny prírastok
 Aký je ročný percentuálny prírastok v meste keď sa za 20 rokov zvýšil počet obyvateľov na trojnásobok?
Aký je ročný percentuálny prírastok v meste keď sa za 20 rokov zvýšil počet obyvateľov na trojnásobok? - Tri ženy
 Uvádza sa, že 72% pracujúcich žien používa počítače pri práci. Vyberte si 3 ženy náhodne a nájdite pravdepodobnosť, že všetky 3 ženy budú pri práci používať počítač.
Uvádza sa, že 72% pracujúcich žien používa počítače pri práci. Vyberte si 3 ženy náhodne a nájdite pravdepodobnosť, že všetky 3 ženy budú pri práci používať počítač. - Podnikateľ 22941
 Podnikateľ Žahourek vložil do banky na účet s 4,5 % ročným úrokom sumu 450 000. Vypočítaj aká čiastka bude na účte po troch rokoch.
Podnikateľ Žahourek vložil do banky na účet s 4,5 % ročným úrokom sumu 450 000. Vypočítaj aká čiastka bude na účte po troch rokoch. - Vkladateľ
 Vkladateľ chce pravidelne na začiatku roka vložiť do peňažného ústavu rovnakú sumu peňazí a na konci desiateho roku chce mať nasporených 10 000 eur. Akú sumu má vkladať, ak ročná úroková miera ročného úrokovacieho obdobia je 2% a daň z úroku je 19 %? Pred
Vkladateľ chce pravidelne na začiatku roka vložiť do peňažného ústavu rovnakú sumu peňazí a na konci desiateho roku chce mať nasporených 10 000 eur. Akú sumu má vkladať, ak ročná úroková miera ročného úrokovacieho obdobia je 2% a daň z úroku je 19 %? Pred - Binárna postupnosť
 V geometrickej postupnosti je dané: kvocient q = 1/2 a súčet prvých šesť členov S6 = 63. Určite piaty prvok a5.
V geometrickej postupnosti je dané: kvocient q = 1/2 a súčet prvých šesť členov S6 = 63. Určite piaty prvok a5.
- Prírastok dreva
 Každým rokom sa v rovnakom čase zisťuje prírastok objemu dreva v lese. Prírastok činí pravidelne p% oproti predchádzajúcemu roku. Ak sa za 10 rokov zväčšil objem dreva o 10%, aké je číslo p?
Každým rokom sa v rovnakom čase zisťuje prírastok objemu dreva v lese. Prírastok činí pravidelne p% oproti predchádzajúcemu roku. Ak sa za 10 rokov zväčšil objem dreva o 10%, aké je číslo p? - Rodinná hypotéka
 Rodina Jonášová sa rozhodla pre kúpu staršieho bytu, ktorý stál 30 000 EUR. Našetrených mali 17 000 EUR a na zvyšnú sumu si zobrali úver v banke. Aký úrok im dala banka, ak uvedenú sumu budú splácať 15 rokov po 120 EUR mesačne?
Rodina Jonášová sa rozhodla pre kúpu staršieho bytu, ktorý stál 30 000 EUR. Našetrených mali 17 000 EUR a na zvyšnú sumu si zobrali úver v banke. Aký úrok im dala banka, ak uvedenú sumu budú splácať 15 rokov po 120 EUR mesačne? - Kocka 2 × 2 × 2
 Kocka 2 × 2 × 2 sa má skonštruovať pomocou 4 bielych a 4 čiernych kociek. Koľko rôznych kociek sa dá takto skonštruovať? (Dve kocky sa nelíšia, ak je možné jednu získať rotáciou druhej. )
Kocka 2 × 2 × 2 sa má skonštruovať pomocou 4 bielych a 4 čiernych kociek. Koľko rôznych kociek sa dá takto skonštruovať? (Dve kocky sa nelíšia, ak je možné jednu získať rotáciou druhej. )
