Rez
Osovým rezom kužeľa, ktorého povrch je 208 m2, je rovnostranný trojuholník. Vypočítajte objem kužeľa.
Správna odpoveď:

Tipy na súvisiace online kalkulačky
Potrebujete pomôcť spočítať, vykrátiť či vynásobiť zlomky? Skúste našu zlomkovú kalkulačku.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Vypočet rovnostranného trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Vypočet rovnostranného trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- aritmetika
- odmocnina
- stereometria
- kúžeľ
- povrch telesa
- planimetria
- Pytagorova veta
- pravouhlý trojuholník
- obsah
- trojuholník
- čísla
- zlomky
- reálne čísla
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Opísaná kružnica
 Vypočítajte polomer kružnice opísaneho trojuholníku, ktorý má rozmery strán 8, 10 a 14cm.
Vypočítajte polomer kružnice opísaneho trojuholníku, ktorý má rozmery strán 8, 10 a 14cm. - Kruh odsek/úsek
 Kruh s priemerom 30 cm je preťať tetivou t = 16 cm. Vypočítajte obvod a obsah menšieho odseku.
Kruh s priemerom 30 cm je preťať tetivou t = 16 cm. Vypočítajte obvod a obsah menšieho odseku. - Polovica obĺžnika
 Vypočítajte obsah pravouhlého trojuholníka ABC s odvesnami a=15cm, b=1,7dm.
Vypočítajte obsah pravouhlého trojuholníka ABC s odvesnami a=15cm, b=1,7dm. - Výška, uhol a strana
 Vypočítajte obsah trojuholníka ABC, v ktorom poznáte stranu c=5 cm, uhol pri vrchole A= 70 stupňov a pomer úsekov, ktoré vytína výška na stranu c je 1:3.
Vypočítajte obsah trojuholníka ABC, v ktorom poznáte stranu c=5 cm, uhol pri vrchole A= 70 stupňov a pomer úsekov, ktoré vytína výška na stranu c je 1:3.
- Obvod 58
 Obvod štvobokého ihlava je 48 m a jeho výška ja 2,5m; koľko bude stáť plech na tento ihlan, keď 1m² stojí 1,5€; do plochy sa počíta aj 12% strata na spoje a záhyby.
Obvod štvobokého ihlava je 48 m a jeho výška ja 2,5m; koľko bude stáť plech na tento ihlan, keď 1m² stojí 1,5€; do plochy sa počíta aj 12% strata na spoje a záhyby. - Rovnoramenný trojuholník -VU
 Vypočítajte dĺžky strán v rovnoramennom trojuholníku, ak je dana výška (na základňu) Vc= 8,8cm a uhol pri zakladni alfa= 38°40`.
Vypočítajte dĺžky strán v rovnoramennom trojuholníku, ak je dana výška (na základňu) Vc= 8,8cm a uhol pri zakladni alfa= 38°40`. - Zastroj
 Zastroj rovnoramenný trojuholník ABY zo základňou AB dĺžky 5 cm a uhlom pri hlavnom vrchole veľkosti 50°. Zapíše postup konštrukcie.
Zastroj rovnoramenný trojuholník ABY zo základňou AB dĺžky 5 cm a uhlom pri hlavnom vrchole veľkosti 50°. Zapíše postup konštrukcie. - Tetiva - uhol
 Je daná kružnica k so stredom v bode S a polomerom 6 cm. Vypočítaj veľkosť stredového uhla, ktorý patí tetive dlhej 10 cm.
Je daná kružnica k so stredom v bode S a polomerom 6 cm. Vypočítaj veľkosť stredového uhla, ktorý patí tetive dlhej 10 cm. - Obsah 44
 Obsah pravouhlému trojuholníka ABC je 346 cm² a uhol pri vrchole A je 64°. Vypočítajte dĺžky odvesien a, b.
Obsah pravouhlému trojuholníka ABC je 346 cm² a uhol pri vrchole A je 64°. Vypočítajte dĺžky odvesien a, b.
- Ťažnice v PT
 V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C sú dané veľkosti ťažníc ta=5, tb=2√10. Vypočítajte veľkosti strán trojuholníka ABC a polomer kružnice opísanej tomuto trojuholníku.
V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C sú dané veľkosti ťažníc ta=5, tb=2√10. Vypočítajte veľkosti strán trojuholníka ABC a polomer kružnice opísanej tomuto trojuholníku. - Daný je 9
 Daný je rovnoramenný trojuholník, ktorého základňa je 8cm a ramená majú dĺžku 15 cm. Vypočítaj obsah trojuholníka a polomer vpísanej a opísanej kružnice.
Daný je rovnoramenný trojuholník, ktorého základňa je 8cm a ramená majú dĺžku 15 cm. Vypočítaj obsah trojuholníka a polomer vpísanej a opísanej kružnice. - Trojuholníku 83150
 V trojuholníku ABC poznáte pomer dĺžok strán a:b:c=3:4:6. Vypočítajte veľkosti uhlov trojuholníka ABC.
V trojuholníku ABC poznáte pomer dĺžok strán a:b:c=3:4:6. Vypočítajte veľkosti uhlov trojuholníka ABC. - Rovnostraný trojuholník
 Vypočítaj stranu rovnostraného trojuholníka, ak jeho obvod je 132 cm.
Vypočítaj stranu rovnostraného trojuholníka, ak jeho obvod je 132 cm. - Rebrík 15
 Rebrík dlhý 6,5 m je opretý o zvislú stenu. Jeho spodný koniec sa opiera o zem vo vzdialenosti 1,6 m od steny. Určte, do akej výšky dosahuje horný koniec rebríka a pod akým uhlom je rebrík opretý o stenu.
Rebrík dlhý 6,5 m je opretý o zvislú stenu. Jeho spodný koniec sa opiera o zem vo vzdialenosti 1,6 m od steny. Určte, do akej výšky dosahuje horný koniec rebríka a pod akým uhlom je rebrík opretý o stenu.
- Deltoid 2
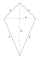 Papierový šarkan má tvar deltoidu ABCD, v ktorom sú dve kratšie strany dlhé po 30 cm, dve dlhšie strany po 51 cm a kratšia uhlopriečka má dĺžku 48 cm. Určte veľkosti vnútorných uhlov daného deltoidu.
Papierový šarkan má tvar deltoidu ABCD, v ktorom sú dve kratšie strany dlhé po 30 cm, dve dlhšie strany po 51 cm a kratšia uhlopriečka má dĺžku 48 cm. Určte veľkosti vnútorných uhlov daného deltoidu. - Stúpanie cesty
 Na dopravnej značke, ktorá informuje o stúpaní cesty, je údaj 6,7 %. Určte uhol stúpania cesty. Aký výškový rozdiel prekonalo auto, ktoré prešlo po tejto ceste 2,8 km?
Na dopravnej značke, ktorá informuje o stúpaní cesty, je údaj 6,7 %. Určte uhol stúpania cesty. Aký výškový rozdiel prekonalo auto, ktoré prešlo po tejto ceste 2,8 km? - Značky
 Dopravné značky majú tvar rovnostranných trojuholníkov s dĺžkou strany 900 mm. Koľko eur stojí pozinkovaný plech na výrobu 50 kusov takýchto značiek, ak na odpad počítame s prídavkom 15% materiálu? Cena 1 meter štvorcový plechu je 6,5 eura.
Dopravné značky majú tvar rovnostranných trojuholníkov s dĺžkou strany 900 mm. Koľko eur stojí pozinkovaný plech na výrobu 50 kusov takýchto značiek, ak na odpad počítame s prídavkom 15% materiálu? Cena 1 meter štvorcový plechu je 6,5 eura.
