Lichoběžník MO-5-Z8
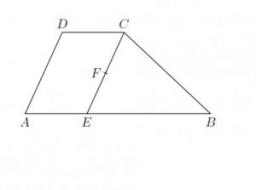
Lichoběžník ABCD je úsečkou CE rozdělen na trojúhelník a rovnoběžník, viz obrázek. Bod F je středem úsečky CE, přímka DF prochází středem úsečky BE a obsah trojúhelníku CDE je 3 cm2.
Určete obsah lichoběžníku ABCD.
Určete obsah lichoběžníku ABCD.
Správná odpověď:
Zobrazuji 2 komentáře:
Tipy na související online kalkulačky
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Čtyřúhelník
 Ukažte, že čtyřúhelník s vrcholy P1 (0,1), P2 (4,2) P3 (3,6) P4 (-5,4) má dva pravé trojúhelníky.
Ukažte, že čtyřúhelník s vrcholy P1 (0,1), P2 (4,2) P3 (3,6) P4 (-5,4) má dva pravé trojúhelníky. - Jak velká
 Jak velká je hnědě vybarvená plocha uvnitř čtverce o straně 6 cm, pokud každá ze čtyř hnědých kruhových úsečí je z kruhu o poloměru délky stany čtverce? Délka kruhových úsečí je rovna délce strany čtverce. Situace je vyobrazena na obrázku vpravo.
Jak velká je hnědě vybarvená plocha uvnitř čtverce o straně 6 cm, pokud každá ze čtyř hnědých kruhových úsečí je z kruhu o poloměru délky stany čtverce? Délka kruhových úsečí je rovna délce strany čtverce. Situace je vyobrazena na obrázku vpravo. - Vypočítejte 22
 Vypočítejte obsah kruhu, který má stejný obvod jako je obvod obdélníku vepsané kružnici o poloměru r 9 cm tak, že jeho strany jsou v poměru 2 ku 7.
Vypočítejte obsah kruhu, který má stejný obvod jako je obvod obdélníku vepsané kružnici o poloměru r 9 cm tak, že jeho strany jsou v poměru 2 ku 7. - Čtverci
 Čtverci o straně a=1 je vepsaná a opsaná kružnice. Určete obsah mezikruží.
Čtverci o straně a=1 je vepsaná a opsaná kružnice. Určete obsah mezikruží.
- Čtvrtkruh
 Jaký poloměr má kruh vepsaný do čtvrtkruhu o poloměru 100 cm?
Jaký poloměr má kruh vepsaný do čtvrtkruhu o poloměru 100 cm? - Valec naležato
 Válec o průměru 3m a výšce/délce 15 m je položen naležato. Je do něj napuštěna voda, která sahá do výšky 60 cm pod osu válce. Kolik hektolitrů vody je ve válci?
Válec o průměru 3m a výšce/délce 15 m je položen naležato. Je do něj napuštěna voda, která sahá do výšky 60 cm pod osu válce. Kolik hektolitrů vody je ve válci? - Rovnoběžníku 5027
 Vypočítejte obsah rovnoběžníku, pokud jsou velikosti stran a=80, b=60 a velikost úhlu sevřeného úhlopříčkami je 60°.
Vypočítejte obsah rovnoběžníku, pokud jsou velikosti stran a=80, b=60 a velikost úhlu sevřeného úhlopříčkami je 60°. - Úseč
 Vypočítejte plochu S úseče a délku kruhového oblouku l. Výška úseče je 2 cm a úhel α = 60°. Pomůcka: S = 1/2 r². (Β-sinβ)
Vypočítejte plochu S úseče a délku kruhového oblouku l. Výška úseče je 2 cm a úhel α = 60°. Pomůcka: S = 1/2 r². (Β-sinβ) - Mezikruží
 Čtverci o obsahu 16 centimetrů čtverečních je vepsaná kružnice k1 a opsána kružnice k2. Vypočtěte obsah mezikruží, které kružnice k1, k2 ohraničují.
Čtverci o obsahu 16 centimetrů čtverečních je vepsaná kružnice k1 a opsána kružnice k2. Vypočtěte obsah mezikruží, které kružnice k1, k2 ohraničují.
- Kruhový bazén
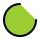 Podstava bazénu má tvar kruhu o poloměru r = 10m kromě kruhového odstavce, který určuje tětiva délky 10m. Jeho hloubka je h = 2m. Kolik hektolitrů vody se vejde do bazénu?
Podstava bazénu má tvar kruhu o poloměru r = 10m kromě kruhového odstavce, který určuje tětiva délky 10m. Jeho hloubka je h = 2m. Kolik hektolitrů vody se vejde do bazénu? - Trojuhelníku 135
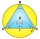 Trojuhelníku ABC o stranách a = 15 cm, b = 17,4 cm, c = 21,6 cm je opsána kružnice. Vypočítejte obsah úsečí určených stranami trojúhelníku.
Trojuhelníku ABC o stranách a = 15 cm, b = 17,4 cm, c = 21,6 cm je opsána kružnice. Vypočítejte obsah úsečí určených stranami trojúhelníku. - V trojúhelníku
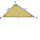 V trojúhelníku ABC vypočítejte velikosti všech výšek, úhlů, obvod a obsah, pokud je dané a-40cm, b-57cm, c-59cm
V trojúhelníku ABC vypočítejte velikosti všech výšek, úhlů, obvod a obsah, pokud je dané a-40cm, b-57cm, c-59cm - Obdélník úhlopříčka
 Vypočtěte obvod a obsah obdélníku, pokud jeho úhlopříčka má délku 14 cm a úhlopříčky svírají úhel 130°.
Vypočtěte obvod a obsah obdélníku, pokud jeho úhlopříčka má délku 14 cm a úhlopříčky svírají úhel 130°. - Plášť 8
 Plášť kužele je vytvořen svinutím kruhové úseče o poloměru 1. Pro jaký středový úhel dané kruhové výseče bude objem vzniklého kužele maximální?
Plášť kužele je vytvořen svinutím kruhové úseče o poloměru 1. Pro jaký středový úhel dané kruhové výseče bude objem vzniklého kužele maximální?
- V pravidelném 2
 V pravidelném čtyřbokem jehlanu je výška 6,5 cm a úhel mezi podstavou a boční stěnou je 42°. Vypočítej povrch a objem tělesa. Výpočty zaokrouhlit na 1 desetinné místo.
V pravidelném čtyřbokem jehlanu je výška 6,5 cm a úhel mezi podstavou a boční stěnou je 42°. Vypočítej povrch a objem tělesa. Výpočty zaokrouhlit na 1 desetinné místo. - Kosý hranol
 Jaký objem má čtyřboký kosý hranol s podstavnými hranami o délce a=1m, b=1,1m, c=1,2m, d=0,7m, jestliže boční hrana o délce h=3,9m má odchylku od podstavy 20°35´ a hrany a, b svírají úhel 50,5°.
Jaký objem má čtyřboký kosý hranol s podstavnými hranami o délce a=1m, b=1,1m, c=1,2m, d=0,7m, jestliže boční hrana o délce h=3,9m má odchylku od podstavy 20°35´ a hrany a, b svírají úhel 50,5°. - Lupínky - kvítek
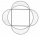 Čtvercu byl opsán kruh a nad každou stranou čtverce, jako nad průměrem, byl vyznačen půlkruh. Vznikly tak 4 lupínky. Co je větší: obsah středního čtverce, nebo obsah čtyř lupínků?
Čtvercu byl opsán kruh a nad každou stranou čtverce, jako nad průměrem, byl vyznačen půlkruh. Vznikly tak 4 lupínky. Co je větší: obsah středního čtverce, nebo obsah čtyř lupínků?
